în anumite circumstanțe, curentul din înfășurarea unui inductor toroidal contribuie numai la câmpul B din interiorul înfășurărilor și nu contribuie la câmpul magnetic B din afara înfășurărilor. Aceasta este o consecință a simetriei și a legii circuitale A amp Otrivre.

condiții suficiente pentru închiderea internă totală a câmpului Bed

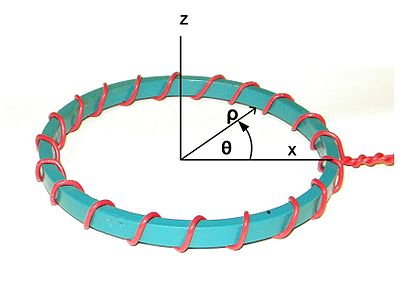fig. 1. Sistem de coordonate. Axa Z este axa nominală de simetrie. Axa X aleasă în mod arbitrar pentru a se alinia cu punctul de plecare al înfășurării. se numește direcția radială. se numește direcția circumferențială.

Fig. 2. Un inductor toroidal simetric axial fără curent circumferențial.

absența curentului circumferențial (calea curentului circumferențial este indicată de săgeata roșie din Figura 3 a acestei secțiuni) și dispunerea simetrică axială a conductorilor și a materialelor magnetice sunt condiții suficiente pentru închiderea internă totală a câmpului B. (Unii autori preferă să utilizeze câmpul H). Datorită simetriei, liniile fluxului B trebuie să formeze cercuri de intensitate constantă centrate pe axa simetriei. Singurele linii de flux B care înconjoară orice curent sunt cele care se află în interiorul înfășurării toroidale. Prin urmare, din Legea circuitală a lui Ampere, Intensitatea câmpului B trebuie să fie zero în afara înfășurărilor.

Fig. 3. Inductor Toroidal cu curent circumferențial

Figura 3 din această secțiune prezintă cea mai comună înfășurare toroidală. Nu reușește ambele cerințe pentru închiderea totală a câmpului B. Privind din Axă, uneori înfășurarea se află în interiorul miezului și alteori se află în exteriorul miezului. Nu este simetric axial în regiunea apropiată. Cu toate acestea, la puncte la o distanță de câteva ori Distanța de înfășurare, toroidul arată simetric. Există încă problema curentului circumferențial. Indiferent de câte ori înfășurarea înconjoară miezul și indiferent cât de subțire este firul, acest inductor toroidal va include în continuare o buclă de bobină în planul toroidului. Această înfășurare va produce și va fi susceptibilă la un câmp E în planul inductorului.

figurile 4-6 prezintă diferite moduri de neutralizare a curentului circumferențial. Figura 4 este cea mai simplă și are avantajul că firul de retur poate fi adăugat după cumpărarea sau construirea inductorului.

Fig. 4. Curent circumferențial contracarat cu un fir de retur. Firul este alb și se desfășoară între marginea exterioară a inductorului și porțiunea exterioară a înfășurării.

Fig. 5. Curent circumferențial contracarat cu o înfășurare de retur.

Fig. 6. Curent circumferențial contracarat cu o înfășurare de retur divizată.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

va exista o distribuție a potențialului de-a lungul înfășurării. Acest lucru poate duce la un câmp E în planul toroidului și, de asemenea, la o susceptibilitate la un câmp E în planul toroidului așa cum se arată în Figura 7. Acest lucru poate fi atenuat prin utilizarea unei înfășurări de retur așa cum se arată în figura 8. Cu această înfășurare, fiecare loc înfășurarea se încrucișează, cele două părți vor fi la polaritate egală și opusă, ceea ce reduce substanțial câmpul E generat în plan.

inductor Toroidal/transformator și vector magnetic potențialedit

arătând dezvoltarea potențialului vector magnetic în jurul unui inductor toroidal simetric.

vezi Feynman Capitolul 14 și 15 pentru o discuție generală a potențialului vectorial magnetic. Vezi Feynman pagina 15-11 pentru o diagramă a potențialului vectorial magnetic în jurul unui solenoid lung subțire care prezintă, de asemenea, închiderea internă totală a câmpului B, cel puțin în limita infinită.

câmpul A este corect atunci când se utilizează ipoteza b f A = 0 {\displaystyle bf{a}=0}

. Acest lucru ar fi adevărat în următoarele ipoteze:

• 1. gabaritul Coulomb este utilizat
• 2. se folosește ecartamentul Lorenz și nu există o distribuție a încărcăturii, 0 {\displaystyle \rho = 0\,}
  
• 3. se folosește ecartamentul Lorenz și se presupune că frecvența zero
• 4. se folosește ecartamentul Lorenz și se presupune o frecvență diferită de zero care este suficient de scăzută pentru a neglija 1 C 2 t {\displaystyle {\frac {1}{C^{2}}}{\frac {\partial \Phi }{\partial t}}
  

  .

numărul 4 va fi prezumat pentru restul acestei secțiuni și poate fi referit la „condiția cvasi-statică”.

deși inductorul toroidal simetric axial fără curent circumferențial limitează total câmpul B în înfășurări, câmpul A (potențial vectorial magnetic) nu este limitat. Săgeata #1 din imagine prezintă potențialul vectorial pe axa simetriei. Secțiunile de curent Radial a și b sunt distanțe egale față de axă, dar îndreptate în direcții opuse, astfel încât acestea se vor anula. De asemenea, segmentele c și d anulează. De fapt, toate segmentele de curent radial anulează. Situația curenților axiali este diferită. Curentul axial din exteriorul toroidului este îndreptat în jos și curentul axial din interiorul toroidului este îndreptat în sus. Fiecare segment de curent axial din exteriorul toroidului poate fi asortat cu un segment egal, dar orientat opus, din interiorul toroidului. Segmentele din interior sunt mai apropiate decât segmentele din exterior de axă, prin urmare există o componentă netă ascendentă a câmpului A de-a lungul axei de simetrie.

reprezentând câmpurile potențial vectorial magnetic (a), flux magnetic (B) și densitate de curent (j) în jurul unui inductor toroidal cu secțiune transversală circulară. Liniile mai groase indică linii de câmp cu intensitate medie mai mare. Cercurile din secțiunea transversală a miezului reprezintă fluxul B care iese din imagine. Plus semne pe cealaltă secțiune transversală a miezului reprezintă flux B merge în imagine. Div a = 0 a fost asumat.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. 0 {\displaystyle {\frac {\partial e}{\partial t}}\rightarrow 0}

) au aceeași formă, apoi liniile și contururile lui A se referă la B ca liniile și contururile lui B se referă la j. astfel, o descriere a câmpului A în jurul unei bucle de flux B (așa cum ar fi produs într-un inductor toroidal) este calitativ același cu câmpul B în jurul unei bucle de curent. Figura din stânga este reprezentarea unui artist a câmpului A în jurul unui inductor toroidal. Liniile mai groase indică căi de intensitate medie mai mare (căile mai scurte au intensitate mai mare, astfel încât integrala căii este aceeași). Liniile sunt desenate doar pentru a arăta bine și pentru a conferi aspectul general al câmpului A.

actiunea transformatorului Toroidal in prezenta limitarii totale a campului B

campurile E si B pot fi calculate din campurile a si B {\displaystyle \Phi\,}

(potential electric scalar) B = A . {\displaystyle \ mathbf {B} =\nabla \ times \ mathbf {A}.}

și : e = − zecimal − zecimal A zecimal t {\displaystyle \mathbf {e} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}

și astfel, chiar dacă Regiunea din afara înfășurărilor este lipsită de câmp B, este umplută cu câmp e diferit de zero. Cantitatea de t {\displaystyle {\frac {\partial \mathbf {a} }{\partial t}}}

este responsabilă pentru cuplarea câmpului magnetic dorit între primar și secundar, în timp ce cantitatea de t {\displaystyle \nabla \phi\,}

este responsabil pentru cuplarea nedorită a câmpului electric între primar și secundar. Proiectanții de transformatoare încearcă să minimizeze cuplarea câmpului electric. Pentru restul acestei secțiuni, {\displaystyle \nabla \phi \,}

se va presupune a fi zero dacă nu se specifică altfel.

teorema Stokes se aplică, astfel încât integrala de cale A lui A este egală cu fluxul B închis, la fel cum integrala de cale B este egală cu o constantă ori curentul închis

integrala de cale a lui E de-a lungul înfășurării secundare dă EMF indus secundar (forța Electro-motrice).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

care spune că EMF este egal cu rata de timp de schimbare a fluxului b închis de înfășurare, care este rezultatul obișnuit.

Transformator Toroidal cuplare vectorială Poynting de la primar la secundar în prezența totală b câmp confinemented

în această figură, punctele albastre indică unde fluxul B din curentul primar iese din imagine și semnele plus indică unde intră în imagine.

explicația figureiedit

această figură prezintă jumătatea secțiunii unui transformator toroidal. Se presupun condiții cvasi-statice, astfel încât faza fiecărui câmp este peste tot aceeași. Transformatorul, înfășurările sale și toate lucrurile sunt distribuite simetric în jurul axei de simetrie. Înfășurările sunt astfel încât nu există curent circumferențial. Cerințele sunt îndeplinite pentru închiderea internă completă a câmpului B datorită curentului primar. Miezul și înfășurarea primară sunt reprezentate de torul gri-maroniu. Înfășurarea primară nu este afișată, dar curentul din înfășurare la suprafața secțiunii transversale este prezentat ca elipse aurii (sau portocalii). Câmpul B cauzat de curentul primar este în întregime limitat la regiunea închisă de înfășurarea primară (adică miezul). Punctele albastre din secțiunea transversală a mâinii stângi indică faptul că liniile fluxului B din miez ies din secțiunea transversală a mâinii stângi. Pe cealaltă secțiune transversală, semnele albastre plus indică faptul că fluxul B intră acolo. Câmpul E provenit din curenții primari este prezentat ca elipse verzi. Înfășurarea secundară este prezentată ca o linie maro care coboară direct pe axa de simetrie. În practica normală, cele două capete ale secundarului sunt conectate împreună cu un fir lung care rămâne departe de torus, dar pentru a menține simetria axială absolută, întregul aparat este imaginat ca fiind în interiorul unei sfere perfect conductive, cu firul secundar „împământat” în interiorul sferei la fiecare capăt. Secundarul este realizat din sârmă de rezistență, deci nu există o sarcină separată. Câmpul E de-a lungul secundarului provoacă curent în secundar (săgeți galbene) care provoacă un câmp B în jurul secundarului (prezentat ca elipse albastre). Acest câmp B umple spațiul, inclusiv în interiorul miezului transformatorului, astfel încât, în cele din urmă, există un câmp B continuu diferit de zero de la primar la secundar, dacă secundarul nu este deschis circuitat. Produsul încrucișat al câmpului E (provenit din curenții primari) și câmpul B (provenit din curenții secundari) formează vectorul Poynting care indică de la primar spre secundar.