revolutionarul Galois Theory

la 31 mai 1832, un revolutionar Republican francez, pe numele sau, a murit in urma unui foc de arma. Avea 20 de ani. Cu o noapte înainte, temându-se de propria moarte, Galois scrisese multe scrisori, mâzgălind frenetic „nu am timp; nu am timp”. O scrisoare este deosebit de prețioasă din motive istorice. În această scrisoare, Galois susține că a declanșat de fapt revoluția. Nu unul politic. Dar unul matematic.
Revoluția inițiată de Galois s-a dovedit a fi mai mare și mai profundă decât și-ar fi putut imagina! Peisajul matematicii a fost profund afectat de viziunea lui Galois, deoarece descendenții săi au crescut și au preluat lumea matematică. Această descendență este acum omniprezentă și stăpânește pământuri nelimitate. Se numește algebră pură.
pentru a romantiza și mai mult povestirea vieții dramatice a lui Galois, iată un rezumat al unui documentar pe care l-am făcut despre algebră:

el este cu siguranta! Dar revoluția lui matematică nu a mers fără probleme. Ca orice lider al revoluției, el a avut mai întâi cele mai mari dificultăți. Nu pentru a imagina Revoluția. Dar pentru a-i convinge pe alții să i se alăture într-o abordare care schimbă jocul matematicii. Când Galois era încă în viață, ideile sale revoluționare au fost respinse de mai multe ori de Academia franceză de științe… pentru că cei mai buni matematicieni francezi din acea vreme, cum ar fi SIM-ul Denis Poisson, nu au putut să-l obțină! Parțial din cauza scrierii de mână necitite a lui Galois afișată în dreapta …
în 1843, la 10 ani de la moartea lui Galois, în cele din urmă, un strălucit matematician francez pe nume Joseph Liouville a reușit să înțeleagă câteva dintre ideile lui Galois. După încă 3 ani de muncă, Liouville a publicat un articol pentru a le explica. Dar articolul lui Liouville era încă prea exagerat pentru ca alți matematicieni să se bucure și să înțeleagă. A fost nevoie de încă 24 de ani pentru a găsi un matematician francez suficient de remarcabil pentru a-l înțelege mai bine pe Galois și pentru a-și face ideile limpezi. Acest matematician remarcabil este Camille Jordan. De fapt, cartea lui Jordan din 1870 despre teoria lui Galois a fost atât de bine scrisă încât matematicianul german Felix Klein a găsit-o la fel de lizibilă ca o carte germană!
a fost cu siguranță un impuls imens. Dar ar mai fi nevoie de încă 82 de ani pentru ca marele matematician austriac Emil Artin să dea în cele din urmă teoriei Galois forma sa modernă, în 1942. Artin merită o mulțime de credite. În timp ce Galois a fost vizionarul care a prevăzut această revoluție, Artin, în multe sensuri, este cel care a întreprins de fapt revoluția și a răsturnat matematica. Mulțumită lui Artin și altor câțiva, astăzi, teoria Galois a devenit o piatră de temelie inevitabilă a cercetării în matematică, cu o mulțime de realizări surprinzătoare și uimitoare (cum ar fi dovada lui Wiles a ultimei teoreme a lui Fermat), precum și un rezervor imens de întrebări deschise și mistere!
câmpuri în algebră pură
teoria Galois este despre simetriile numerelor. Dar înainte de a ajunge acolo, am nevoie să introducă pentru a te înarmat de permițându-vă pe un secret despre numere. Și sunt sigur că ai auzit de ea! Într-adevăr, în liceu, probabil că ați fost învățați să nu lăsați niciodată rădăcini în numitori.
vreau să spun că $1 / (\sqrt{2}-1)$ nu a fost un răspuns corect. Puteți ajuta să scăpați de rădăcina pătrată a 2 în numitor?
Hehe… am fost învățați să se înmulțească în sus și în jos prin conjugatul numitorului. Acest conjugat este obținut prin înlocuirea $ – $ cu $ + $ (sau invers) în numitor:
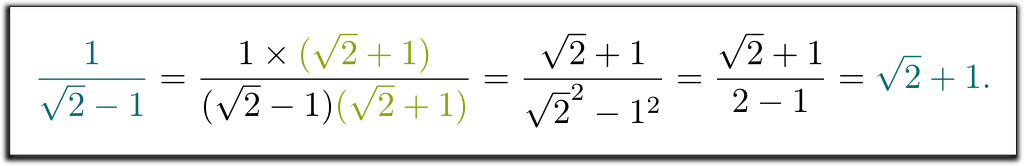
știu! Expresia complicată $1 / (\sqrt{2}-1) $reprezintă același număr ca$\sqrt{2}+1$. Și asta explică de ce profesorii noștri au vrut să scriem rezultate într-un fel, mai degrabă decât în celălalt: când totul este scris în același mod, examenele devin mult mai ușor de corectat!
dar ce zici de $1 / (\sqrt{2}-1)$? Poți să scapi de rădăcină în numitor? Se poate face chiar?
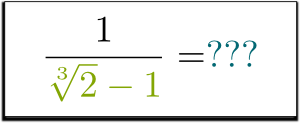
știu!
spune-mi!
ceva noroc?
Hehe… interesant, orice putere de $ \ sqrt{2}-1$ poate fi scrisă ca o sumă de puteri de $\sqrt{2}$. Într-adevăr, trebuie doar să distribuiți produsele:
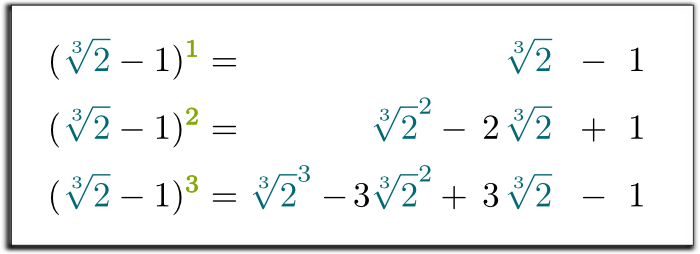
da, este! Făcând această substituție în a treia ecuație, am arătat că cele trei prime puteri ale $ \ sqrt{2}-1$ pot fi scrise ca o sumă a unui număr rațional, de $ \ sqrt{2}$ și de $ \ sqrt{2}^2$!
deci, avem acum 3 ecuații, cu 2 expresii rădăcină vrem să scăpăm! Astfel, putem combina ecuațiile pentru a elimina toate expresiile rădăcină din dreapta!
să înmulțim primele 2 linii cu 3 și să adunăm toate cele 3 ecuații:
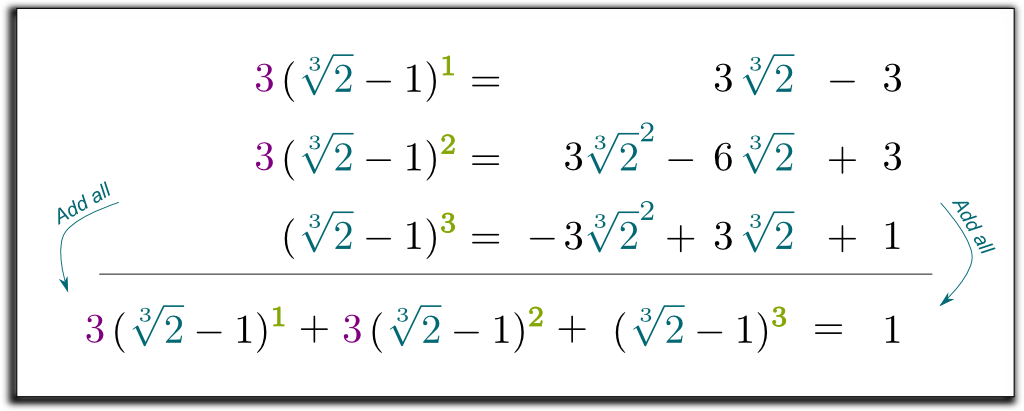
Hehe… interesant este că termenul din stânga pe care l-am obținut poate fi acum factorizat prin $\sqrt{2}-1$! Permiteți-mi să sar peste unele calcule plictisitoare … și ajunge la rezultatul $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Deci, pentru a scăpa de rădăcinile din numitor, putem înmulți în sus și în jos cu $\sqrt{2}^2 + \sqrt{2} + 1$! În cele din urmă, obținem următoarea formulă surprinzătoare și frumoasă:
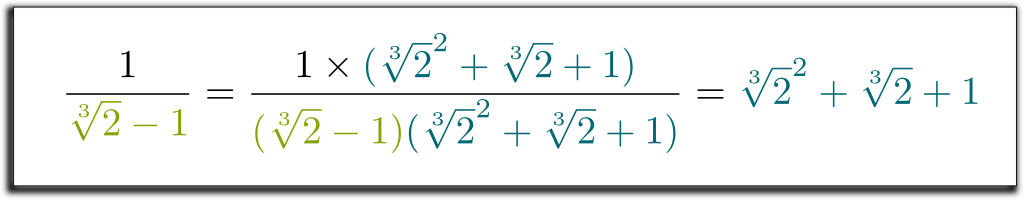
știu! Dar ceea ce este și mai ordonat este că metoda pe care am folosit-o este foarte generală! Cu tehnici similare, acum putem elimina toți radicalii de la numitori!
este comun pentru a desemna $\mathbb Q{2}]$ setul de numere care pot fi scrise ca o sumă de puteri de $\sqrt{2}$. Deoarece $ \ sqrt{2}^3 = 2$ este un număr rațional, orice sumă de puteri de $\sqrt{2}$ poate fi de fapt scrisă în forma standard $a\sqrt{2}^2 + b\sqrt{2} + c$. Acum, dacă adăugați, scădeți sau înmulțiți oricare două astfel de numere, atunci nu este greu să vedem că obținem numere care pot fi încă puse în forma standard $a\sqrt{2}^2 + b\sqrt{2} + c$. În plus, ceea ce tocmai am arătat aici este că inversul tuturor numerelor $a\sqrt{2}^2 + b\sqrt{2} + C$ poate fi scris și în formă standard. Aceasta arată că orice adunare, scădere, înmulțire și împărțire a numerelor în $\mathbb Q{2}]$ produce un număr, care poate fi scris în formă standard… și astfel aparține $\mathbb Q{2}]$. În termeni de algebră pură, $ \ mathbb Q{2}]$ este astfel stabil prin cele patru operații aritmetice clasice. Din acest motiv, îl numim câmp.
geometria extensiilor de câmp
câmpul cu care sunteți cel mai familiarizat este probabil setul $\mathbb Q$ al numerelor raționale. Alte exemple de câmpuri sunt seturile $\mathbb R$ de numere reale și setul $\mathbb C$ de numere complexe. Și acum, avem și $ \ mathbb Q{2}]$. Deoarece $ \ mathbb Q{2}]$ este un câmp care conține câmpul $ \ mathbb Q$, spunem că $ \ mathbb Q{2}] / \mathbb Q$ este o extensie de câmp.
faptul că $\mathbb Q{2}] / \mathbb Q$ este o extensie de câmp produce o conexiune foarte naturală între cele două câmpuri. Și anume, $ \ mathbb Q{2}]$ poate fi văzut ca un spațiu vectorial, unde $\mathbb Q$ este câmpul scalar. În special, faptul că orice număr din $\mathbb Q{2}]$ poate fi scris $a \sqrt{2}^2 + b\sqrt{2} + c$ înseamnă că $(1, \sqrt{2}, \sqrt{2}^2)$ formează baza $\mathbb Q{2}]$ ca spațiu vectorial $\mathbb Q$. Și asta înseamnă că îl putem reprezenta geometric ca un spațiu cu 3 dimensiuni!
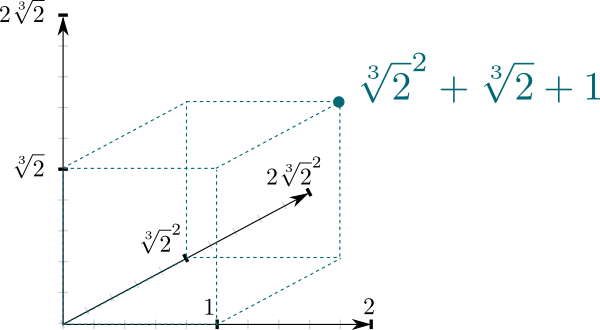
dimensiunea spațiului vectorial de mai sus este o proprietate interesantă a extensiilor de câmp. Este cunoscut sub numele de grad și este denumit în mod obișnuit $\big{2}] : \mathbb Q\big] = 3$ de exemplu.
Da! De fapt, este destul de ușor să creați o extensie de câmp a acestui lucru: trebuie doar să adăugați un număr radical care nu aparține $\mathbb Q{2}]$!
Da! Aceasta ar crea câmpul $(\mathbb Q{2}]) = \mathbb Q{2}, \ sqrt{2}]$. Aceste câmpuri conțin toate numerele care sunt produse și sume de $\sqrt{2}$ și $ \ sqrt{2}$. Acestea sunt de forma $a \ sqrt{2}^2$ + $b \ sqrt{2} + c$ + $ D \ sqrt{2}^2 \ sqrt{2} $ + $ e \ sqrt{2} \ sqrt{2} $ + $ f \ sqrt{2}$. Ai idee care este gradul $ \ big{2}, \ sqrt{2}]:\mathbb Q{2}] \ big]$?
Da! Într-adevăr, avem $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ D\sqrt{2}^2\sqrt{2} \sqrt{2} $ + $ f \sqrt{2} $ = $ (a \sqrt{2}^2 + b\sqrt{2}+c) $ + $ (d\sqrt{2}^2 + e\sqrt{2} + F) \sqrt{2}$. Astfel, orice număr de $ \ mathbb Q{2},\sqrt{2}]$ poate fi scris $A+B\sqrt{2}$, unde $a$ și $B$ aparțin $\mathbb Q{2}]$. Astfel, 2 scalari de $ \ mathbb Q{2}] $ determină un număr în $ \ mathbb Q{2},\sqrt{2}]$. Aceasta înseamnă că gradul extensiei câmpului $ \ mathbb Q{2}, \sqrt{2}] / \ mathbb Q{2}]$ este 2. De fapt, avem relația Chasles $\big{2}, \ sqrt{2}]: \ mathbb Q \ big] $ = $ \ big{2}, \ sqrt{2}] : \mathbb Q{2}] \mare] \mare{2}] : \mathbb Q \mare] $=$ 2 \ori 3 = 6$.
e mai bine de atât! Orice extensie de câmp de grad finit, numită extensie de câmp finit, este întinsă de un singur număr. De exemplu $\mathbb Q{2}, \sqrt{2}] $ = $ \mathbb Q{2} + \sqrt{2}]$, ceea ce înseamnă că toate numerele care sunt sume de puteri de $\sqrt{2}$ și $\sqrt{2}$ sunt, de asemenea, sume de puteri de $\sqrt{2} + \ sqrt{2}$. Nu este surprinzător de minunat?
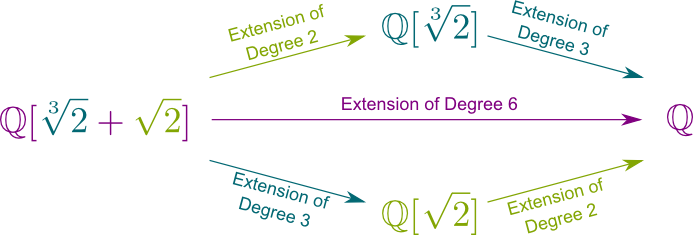
Mai general, orice extensie de câmp finit de $\mathbb Q$ poate fi scris $\mathbb Q$ cu unele $x$ care se adaugă la $\mathbb Q$.
Da. Este cazul extensiei de câmp $ \ mathbb R / \ mathbb Q$. Și, așa este cea mai importantă extensie de câmp în teoria Galois! Această extensie de câmp este $ \ bar {\mathbb Q} / \ mathbb Q$, unde $ \ bar {\mathbb Q} $ este setul de numere algebrice. Acestea sunt toate soluțiile la ecuațiile polinomiale ale formei $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $ + $ a_0 = 0$. De exemplu, $\sqrt{2}$ este un număr algebric, deoarece este o soluție la $x^4 – 2x = 0$. Astfel, $ \ bar {\mathbb Q}$ este o extensie de câmp la Toate extensiile de câmp finite ale $ \ mathbb Q$.
numere Conjugate
suntem aproape acolo! Avem nevoie de un ocol final prin ecuații polinomiale.

exact! Galois a observat că unele ecuații ar putea fi simplificate. De exemplu, $x^4-2x=0$ poate fi factorizat ca $x(x^3-2)=0$, ceea ce corespunde $x=0$ sau $x^3-2=0$. Deci, ecuația $ x^4-2x=0$ poate fi redusă la ecuații $x=0$ și $X^3-2=0$. Și, de fapt, această reducere este foarte asemănătoare cu modul în care numerele precum 35 pot fi reduse la 5 și 7, deoarece $5 \times 7 = 35$. Asemănarea dintre ecuații și numere întregi este atât de puternică încât putem face chiar diviziuni euclidiene de polinoame, la fel cum ați învățat să o faceți pentru numere! În dreapta este un exemplu de astfel de diviziune (nu vă faceți griji dacă nu o înțelegeți, nu va fi important pentru continuare).deci, cred că Galois a studiat echivalentul numerelor prime …
exact! Acestea sunt cunoscute sub numele de ecuații polinomiale ireductibile. Ecuația $ x^3-2 = 0$ este un exemplu de ecuație polinomială ireductibilă.
Da! Dar, în mod crucial, Galois a vrut să se concentreze pe ecuații cu coeficienți raționali. Sau, mai degrabă, polinoame cu coeficienți care aparțin câmpului de bază. Deci, ceea ce am vrut să spun a fost că, pentru $\mathbb Q$ ca câmp de bază, $x^3-2=0$ este ireductibil.
să luăm în considerare $x^2 – 2x -1=0$ pentru a avea câteva indicii. Această ecuație poate fi dovedită a fi ireductibilă. Îți amintești cum să o rezolvi?
Dacă $ b^2-4AC \ geq 0$, Da.
exact! Deci, ecuația polinomială ireductibilă $x^2 + 2x -1 = 0$ are două soluții: $1 + \sqrt{2}$ și $1-\sqrt{2}$… Orice comentariu?
Bingo! Aceasta este descoperirea cheie a lui Galois. Mai general, Galois numit conjugă toate soluțiile la o ecuație polinomială ireductibilă. Și, după cum vă puteți imagina, acestea sunt esențiale pentru a elimina radicalii de la numitori!
primul lucru de observat este că dacă $x_1$, $x_2$, …, $x_n$ sunt toate soluțiile unei ecuații ireductibile polinomiale $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ cu coeficienți raționali, atunci această ecuație ireductibilă polinomială poate fi rescrisă $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Identificarea Termenilor constanți produce apoi $ x_1 x_2 … x_n $ = $ (-1)^n a_0 / a_n$. Deci, în mod crucial, produsul numerelor conjugate este numărul rațional $(-1)^n a_0/a_n$, care este diferit de zero (dovedește-o!).pentru a face ceea ce tocmai am spus, soluțiile ecuațiilor polinomiale ireductibile trebuie să aibă multiplicitate 1. Această proprietate este cunoscută sub numele de separabilitate. Această proprietate depinde numai de câmpul de bază. Câmpurile de bază ale căror polinoame ireductibile sunt separabile se numesc perfecte. Din fericire, în cazul nostru, $ \ mathbb Q$ este perfect, precum și Toate extensiile sale.
Iată o mică glumă pentru a ține cont de legătura puternică dintre conjugați:

luați în considerare o fracție $1 / x_1$, unde $x_1$ este o expresie complicată cu radicali. Înmulțirea în sus și în jos cu conjugații $x_2$,…, $x_n$ de $ x_1 $ apoi produce $1/x_1 $=$ (-1)^n a_n x_2…x_n / a_0$, care nu are radical în numitor așa cum am stabilit $a_0$ să fie un număr diferit de zero al câmpului de bază!
reamintim că $x ^ 3-2 = 0$ este ecuația polinomială ireductibilă $\sqrt{2}$ este soluția lui. Deci, conjugatele sale sunt celelalte soluții la acea ecuație, care sunt numerele complexe $\sqrt{2}j$ și $\sqrt{2}j^2$, unde $j= e^{I\tau/3}$ cu $\tau = 2\pi$ fiind raportul circumferinței unui cerc după raza sa. Următoarea figură afișează locațiile soluțiilor conjugate în acest plan complex:
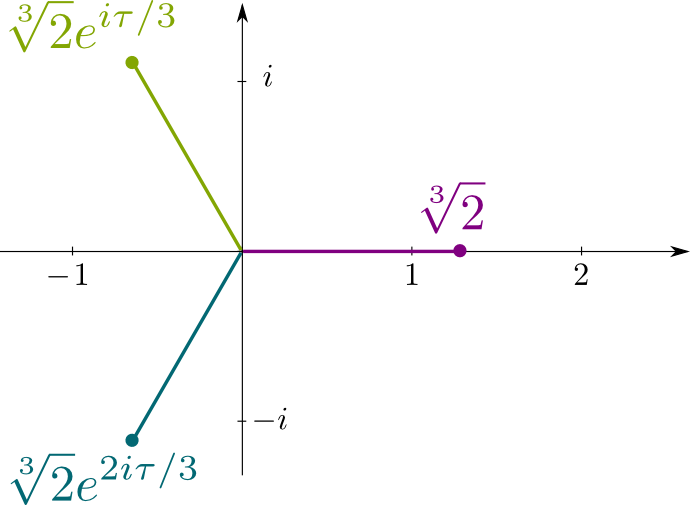
ambiguitatea lui Galois
În cele din urmă, ajungem la înțelegerea cheie a lui Galois!
conjugatele sunt perfect permutabile. Aceasta înseamnă că, dacă schimbați sistematic $\sqrt{2}$ prin conjugatul său $-\sqrt{2}$, atunci egalitățile rămân în continuare. De exemplu, din moment ce am avut $1 / (\sqrt{2}-1)=\sqrt{2}+1$, pot să vă spun direct că $1/(-\sqrt{2}-1) = -\sqrt{2}+1$! În mod similar, avem următoarele implicații uimitoare:
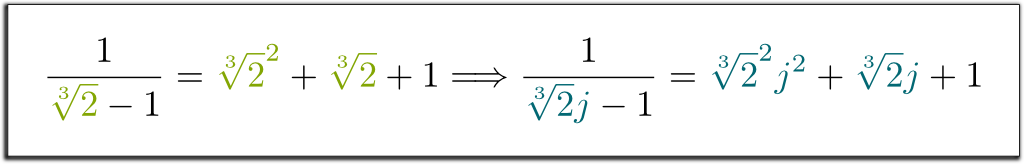
Hehe… permiteți-mi să amintesc mai întâi că câmpurile finite sunt întinse de un singur element. Deci, dacă câmpul de bază este $\mathbb Q$, orice câmp finit poate fi scris $\mathbb Q$ pentru un drept $x_1$. Acum, ia în considerare $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ ecuația polinomială ireductibilă $x_1$ este soluția. Apoi, ceea ce definește $\mathbb Q$ este $\mathbb Q$-spațiu vectorial cuprins de $x_1$, $x_1^2$,…, $x_1^{n-1}$, cu simplificarea puterilor mai mari de $x_1$ în conformitate cu regula algebrică $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.
exact! În mod crucial, aceste reguli algebrice ale $ \ mathbb Q$ nu depind cu adevărat de natura $x_1$; ele depind doar de polinomul ireductibil $x_1$ este soluția! Prin urmare, regulile $\mathbb Q$ sunt identice cu cele ale $\mathbb Q$,…, $\mathbb Q$, unde $x_1$ este înlocuit cu unul dintre conjugații săi $x_2$,…, $x_n$. În special, câmpurile $ \ mathbb Q{2}]$ și $ \ mathbb Q{2} j] $ funcționează conform acelorași reguli. De aceea conjugatele sunt perfect permutabile! Spunem că câmpurile $ \ mathbb Q{2}]$ și $\mathbb Q{2} j]$ sunt izomorfe și că înlocuirea $\sqrt{2}$ cu $\sqrt{2}j$ este un izomorfism $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.
într-un mod foarte similar (dar mai puternic) că două spații vectoriale de dimensiunea 2 sunt mai mult sau mai puțin la fel! Aceasta are o consecință teribilă. Înseamnă că, dintr-o perspectivă algebrică, nu are sens să faci o diferență între un număr și oricare dintre conjugatele sale (atâta timp cât înlocuiești sistematic numărul cu conjugatul său)! Deci, de exemplu, $\sqrt{2}$ și $ – \sqrt{2} $ sunt algebric imposibil de distins! Pentru a ține cont de acest lucru, iată o altă glumă cu care am venit:

deloc! Orice distincție între aceste două numere trebuie să implice o altă matematică decât algebra, cum ar fi relațiile de ordine sau topologia. Ceea ce vreau să spun este că, de exemplu, relația $\sqrt{2} > 0$ face o diferență între $\sqrt{2}$ de $-\sqrt{2}$, dar asta pentru că implică o relație de ordine. Dar dacă ne limităm la egalități polinomiale,atunci nu există absolut nicio diferență între $\sqrt{2}$ și $ – \sqrt{2}$. În mod similar, $i$ și $-i$, soluțiile ecuației polinomiale ireductibile $x^2+1=0$, sunt, de asemenea, indistinguibile algebric. Cu toate acestea, numim arbitrar $i$ unul dintre ei. Acesta este motivul pentru care Galois a numit teoria sa teoria ambiguității. Astăzi, ambiguitatea alegerii rădăcinii pătrate convenționale de $-1$ între $i$ și $ – i$ este mai degrabă numită simetria dintre $i$ și $ – i$.
grupuri Galois
Galois s-a concentrat în special pe extensiile de câmp care sunt stabile prin conjugare. Astfel de extensii de câmp stabile sunt acum cunoscute sub numele de extensii Galois. Deci, dacă $x_1 $ aparține unei extensii Galois, atunci această extensie Galois conține toate conjugatele sale $x_2$,…, $x_n$.
o modalitate simplă de a construi extensii Galois constă în luarea câmpului cuprins de soluții ale unei ecuații polinomiale ireductibile. De exemplu, dacă $x_1$,…, $x_n$ sunt conjugați pentru câmpul de bază $\mathbb Q$, atunci $\mathbb Q / \mathbb Q$ este o extensie Galois. Câmpurile construite în acest fel se numesc câmpuri de divizare.
de exemplu, câmpul de divizare al ecuației $x^3-2=0$ este extensia Galois $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ întinsă de soluțiile sale.
dacă $x_1$ se întinde pe o extensie Galois, atunci și conjugatele sale. Astfel, $ \ mathbb Q = \ mathbb Q = $ … $ = \ mathbb Q$ = $ \ mathbb Q$. Astfel, izomorfismul dintre $ \ mathbb Q$ și $ \ mathbb Q$ care constă în înlocuirea întotdeauna $x_1$ cu $x_2$ este de fapt un izomorfism între $\mathbb Q$ și el însuși! Îl numim automorfism. Automorfismele unei extensii Galois $ \ mathbb Q / \ mathbb Q $ formează grupul Galois $Gal (\mathbb Q/ \ mathbb Q)$.
acum, crucial, dacă $ \ mathbb Q = \ mathbb Q$, atunci toate automorfismele unei extensii Galois $ \ mathbb Q / \ mathbb Q$ sunt permutări de $x_1$ cu unul dintre conjugații săi! În special, vedem aici că cardinalitatea unui grup Galois este egală cu gradul extinderii Galois.
sigur! Puteți observa că $ \ mathbb Q = \ mathbb Q $ și $ \ mathbb Q = \ mathbb Q$, ceea ce înseamnă că $i$ și $\sqrt{2}$ fiecare se întinde pe câmpurile de divizare ale ecuației polinomiale ireductibile de care sunt soluții. Astfel, $ \ mathbb Q / \ mathbb Q$ și $ \ mathbb Q / \ mathbb Q$ sunt ambele extensii Galois. Prin urmare, automorfismele lor constau în înlocuirea $i$ cu unul dintre conjugații săi, $i$ sau $-i$ și înlocuirea $\sqrt{2}$ cu $\sqrt{2}$ sau $-\sqrt{2}$. În primele cazuri, nu schimbăm nimic în numere, ceea ce corespunde simetriei zero. Al doilea caz poate fi vizualizat ca simetrii axiale, așa cum se arată în figura de mai jos:

nu este uimitor?
sigur! Să ajungem la câmpul de divizare $ \ mathbb Q{2}, \ sqrt{2}j, \ sqrt{2}j ^ 2] $ de $ x ^ 3-2 = 0$. Dar, înainte de a merge mai departe, să observăm că $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.
Hehe… pentru a înțelege simetriile $ \ mathbb Q{2}]$, va trebui să mergem mai departe în studiul lui Galois asupra grupurilor Galois…
corespondența Galois
problema cu grupurile Galois este că ele pot deveni extrem de mari și complicate. Acesta este în special cazul grupului infinit $Gal(\bar{\mathbb Q}/\mathbb Q)$. Pentru a prinde astfel de grupuri uriașe și complexe, Galois a avut ideea genială de a le sparge în bucăți mai mici.
știu! Îmi place să vizualizez aceste simetrii ca modalități de a conecta $\mathbb Q{2},j]$ pe $\mathbb Q$. Iată o imagine imaginată a „conectării la”:
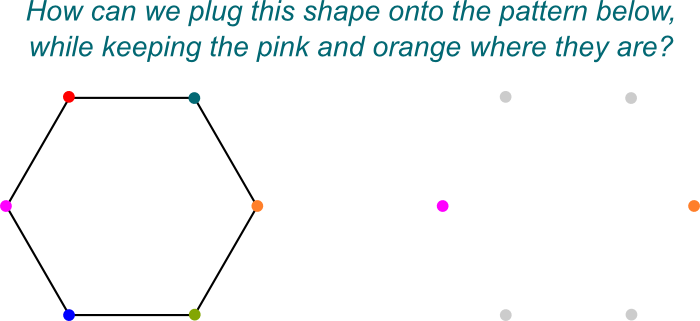
exact! Și asta pur și simplu pentru că $\mathbb Q{2},j]$ este o extensie Galois a $\mathbb Q$ care este ea însăși o extensie de câmp a $\mathbb Q$.
și nu e mai mult! Galois a arătat că toate subgrupurile unei extensii Galois sunt obținute în acest fel! Mai precis, maparea oricărui câmp $K$ între extensia Galois $ \ mathbb Q{2},j]$ și câmpul de bază $\mathbb Q$ la grupul Galois $Gal(\mathbb Q{2},j] / K)$ este bijectivă. Acest fapt se numește corespondența Galois! Această corespondență este afișată schematic mai jos pentru o extensie Galois $\mathbb Q/\mathbb Q$.

în loc să încercăm să descriem direct acest grup, să ne concentrăm pe subgrupul său $Gal(\mathbb Q{2}, j] / \mathbb Q)$. Este simplu că $ \ sqrt{2} $ se întinde pe $ \ mathbb Q{2}, j]$ când este adăugat la $ \ mathbb Q$. Astfel, $ \ mathbb Q{2}, j] / \ mathbb Q$ este o extensie Galois întinsă de $ \ sqrt{2}$. Prin urmare, folosind o teoremă pe care am văzut-o mai devreme, știm că toate automorfismele acestei extensii Galois constau în înlocuirea $\sqrt{2}$ cu unul dintre cei 3 conjugați ai săi (în sine, $\sqrt{2} j$ și $\sqrt{2} J^2$)!
acum, aș putea continua să studiez alte piese de $Gal(\mathbb Q{2}, j]/\mathbb Q)$, cum ar fi subgrupul Galois $Gal(\mathbb Q{2},j] / \mathbb Q{2}])$. Dar voi folosi mai degrabă o altă teoremă puternică a lui Galois. Anume, el a dovedit că dacă $\mathbb Q/\mathbb Q$ A fost în plus o extensie Galois în sine, atunci subgrupul $Gal(\mathbb Q{2}, j]/\mathbb Q)$ este normal.
astfel, grupul Galois din $\mathbb Q{2},j]/\mathbb Q$ poate fi cotat de acest subgrup, iar grupul coeficient este egal cu $Gal(\mathbb Q / \mathbb Q)$. Cu toate acestea, $\mathbb Q/\mathbb Q$ este într-adevăr o extensie Galois întinsă de $j$, al cărei conjugat este $j^2$. Astfel, $Gal (\mathbb Q/ \ mathbb Q)$ constă fie în părăsirea $j$ ca $j$ sau înlocuirea acestuia cu $j^2$.
putem deduce acum toate simetriile $Gal(\mathbb Q{2},j]/\mathbb Q)$ prin combinarea acestora de $Gal(\mathbb Q{2},j] / \mathbb Q)$ și $Gal(\mathbb Q/\mathbb Q)$. Putem afișa aceste simetrii desenând modul în care acestea afectează cele trei conjugate de acoperire $\sqrt{2}$, $\sqrt{2}j$ și $\sqrt{2}j^2$:
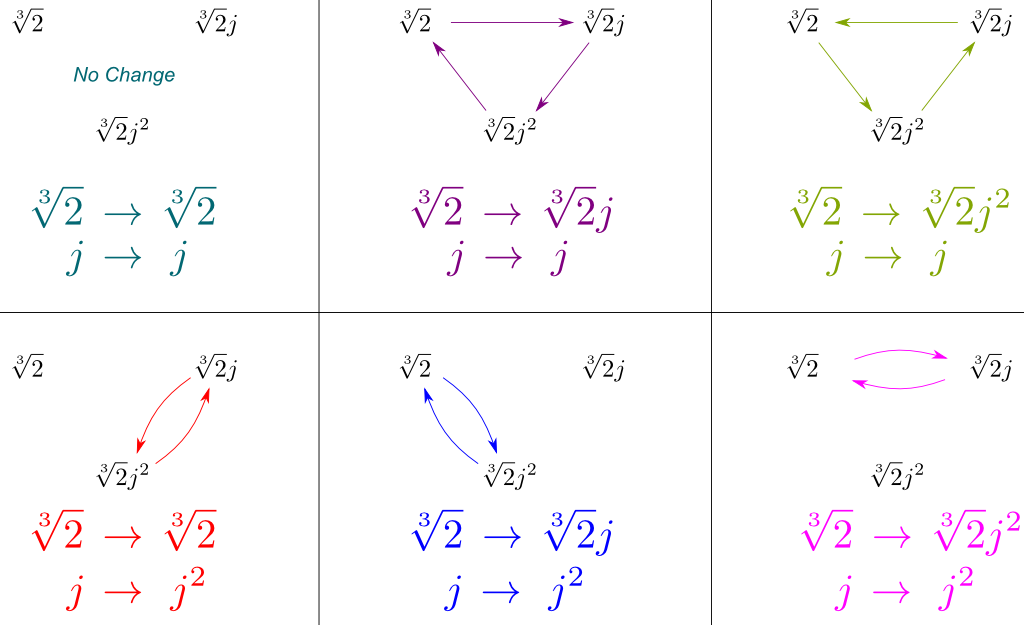
în mod crucial, figura de mai sus conține toate simetriile $Gal(\mathbb Q{2},j] / \mathbb Q)$. Și uimitor, aceste simetrii corespund bine-cunoscut grup de simetrie.
îl voi lăsa pe Marcus du Sautoy să ți-l prezinte:deci, simetriile sunt aici ca o stea de mare sau ca un triunghi?
da, într-adevăr! Acest grup de simetrii ale triunghiului se numește $D_3$ și este același cu grupul $s_3$ de permutări de 3 elemente. Acest lucru ne conduce la următoarea formulă, pe care am găsit-o atât de frumoasă, încât am decis să o încadrez!
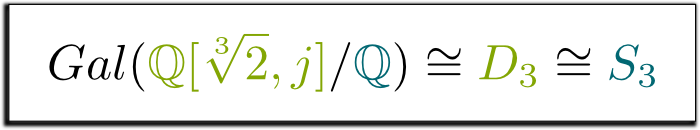
să concluzionăm
în multe privințe, Galois trebuie considerat părintele algebrei moderne. Înțelegerea sa cheie a fost să privească matematica prin unghiul regulilor operațiilor, iar acest lucru l-a determinat să dezvăluie ambiguități surprinzătoare și perspicace, sau simetrii, între numere. Dintr-o perspectivă algebrică, numere precum $\sqrt{2}$, $\sqrt{2}j$ și $\sqrt{2}j^2$ sunt într-adevăr perfect simetrice și total interschimbabile.
înțelegerea acestor simetrii a avut aplicații uimitoare în geometria algebrică și topologia algebrică, printre altele. În special, succesele timpurii ale teoriei includ o clasificare a poligoanelor regulate constructibile și o teoremă care afirmă că ecuațiile polinomiale de grad înalt nu ar putea fi rezolvate de radicali.
succesele recente apar în criptografie și dovada lui Andrew Wiles a ultimei teoreme a lui Fermat. Această dovadă implică studierea grupului Galois $Gal (\bar {\mathbb Q} / \ mathbb Q)$ cu reprezentarea grupului. Dar aș spune că teoria este într-un fel încă tânără și mai sunt multe de descoperit. La urma urmei, este unul dintre cele mai active domenii de cercetare în cercetarea matematică pură de astăzi.
asta ar trebui să ne facă să aducem mult mai multe omagii incredibilului geniu al lui Galois… permiteți-mi să includ unul de SocraticaStudios.