filtre Kalman

algoritmul folosit pentru a îmbina datele se numește filtru Kalman.

filtrul Kalman este unul dintre cei mai populari algoritmi în fuziunea datelor. Inventat în 1960 de Rudolph Kalman, acum este folosit în telefoanele sau sateliții noștri pentru navigație și urmărire. Cea mai faimoasă utilizare a filtrului a fost în timpul misiunii Apollo 11 de a trimite și aduce echipajul înapoi pe lună.

când să folosiți un filtru Kalman ?

un filtru Kalman poate fi utilizat pentru fuziunea datelor pentru a estima starea unui sistem dinamic (evoluând cu timpul) în prezent (filtrare), trecut (netezire) sau viitor (predicție). Senzorii încorporați în vehicule autonome emit măsuri care sunt uneori incomplete și zgomotoase. Inexactitatea senzorilor (zgomotul) este o problemă foarte importantă și poate fi gestionată de filtrele Kalman.

un filtru Kalman este utilizat pentru a estima starea unui sistem, notat x. acest vector este compus dintr-o poziție p și o viteză v.

starea unui sistem

la fiecare estimare, asociem o măsură de incertitudine P.

prin efectuarea unei fuziuni de senzori, luăm în considerare date diferite pentru același obiect. Un radar poate estima că un pieton este la 10 metri distanță, în timp ce Lidar estimează că este la 12 metri. Utilizarea filtrelor Kalman vă permite să aveți o idee precisă pentru a decide câți metri este într-adevăr pietonul prin eliminarea zgomotului celor doi senzori.

un filtru Kalman poate genera estimări ale stării obiectelor din jurul său. Pentru a face o estimare, este nevoie doar de observațiile actuale și de predicția anterioară. Istoricul măsurătorilor nu este necesar. Prin urmare, acest instrument este ușor și se îmbunătățește cu timpul.

cum arată

starea și incertitudinea sunt reprezentate de Gaussieni.

Gaussian

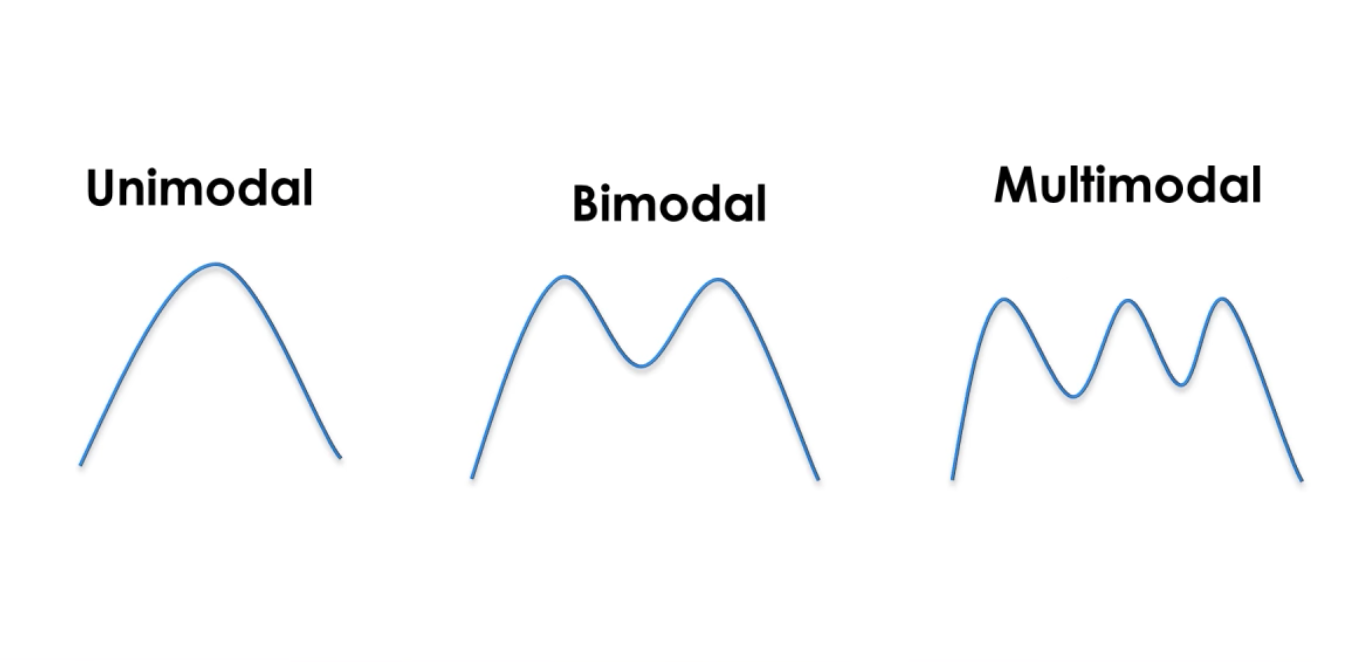
un Gaussian este o funcție continuă sub care zona este 1. Acest lucru ne permite să reprezentăm probabilitățile. Suntem pe o probabilitate de distribuție normală. Uni-modalitatea filtrelor Kalman înseamnă că avem un singur vârf de fiecare dată pentru a estima starea sistemului.

Avem o medie μ reprezintă un stat și o varianță σ2 reprezintă o incertitudine. Cu cât varianța este mai mare, cu atât este mai mare incertitudinea.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Folosim observațiile senzorilor noștri pentru a corecta starea prezisă și pentru a obține o estimare mai precisă.

pentru a face o estimare, un filtru Kalman are nevoie doar de observații curente și de predicția anterioară. Istoricul măsurătorilor nu este necesar.

matematică

matematica din spatele filtrelor Kalman este formată din adăugiri și multiplicări de matrice. Avem două etape: predicție și actualizare.predicția noastră constă în estimarea unei stări x ‘și a unei incertitudini P’ la momentul t din stările anterioare x și P la momentul t-1.

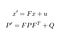
• f: matrice de tranziție de la t-1 la t
• : Matricea de covarianță, inclusiv zgomotul

actualizare
faza de actualizare constă în utilizarea unei măsurători z de la un senzor pentru a corecta predicția noastră și astfel a prezice X și P.

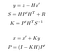
• y: diferența dintre Măsurarea reală și predicție, adică eroarea.
• S: eroare de sistem estimată
• H: matricea de tranziție între markerul senzorului și al nostru.
• R: Matricea de covarianță legată de zgomotul senzorului (dată de producătorul senzorului).
• K: Kalman gain. Coeficient între 0 și 1 care reflectă necesitatea corectării predicției noastre.

faza de actualizare face posibilă estimarea unui x și a unui P Mai aproape de realitate decât ceea ce oferă măsurătorile.

un filtru Kalman permite predicții în timp real, fără date în prealabil. Folosim un model matematic bazat pe multiplicarea matricelor pentru fiecare dată când definim o stare x (poziție, viteză) și incertitudine P.

retipărire/retipărire înainte / Posterior

această diagramă arată ce se întâmplă într-un filtru Kalman.

estimarea filtrului Kalman (sursă)

• estimarea stării prezise reprezintă prima noastră estimare, faza noastră de predicție. Vorbim despre prior.
• măsurarea este măsurarea de la unul dintre senzorii noștri. Avem o incertitudine mai bună, dar zgomotul senzorilor îl face o măsurare care este întotdeauna dificil de estimat. Vorbim despre probabilitate.
• estimarea optimă a stării este faza noastră de actualizare. Incertitudinea este de data aceasta cea mai slabă, am acumulat informații și am permis să generăm o valoare mai sigură decât doar cu senzorul nostru. Această valoare este cea mai bună presupunere a noastră. Vorbim de posterior.

ceea ce implementează un filtru Kalman este de fapt o regulă Bayes.

regula Bayes

într-un filtru Kalman, buclăm predicțiile din măsurători. Predicțiile noastre sunt întotdeauna mai precise, deoarece păstrăm o măsură de incertitudine și calculăm în mod regulat eroarea dintre predicția noastră și realitate. Suntem capabili de multiplicări matrice și formule de probabilitate pentru a estima vitezele și pozițiile vehiculelor din jurul nostru.

filtre”extinse/fără parfum” și neliniaritate

apare o problemă esențială. Formulele noastre matematice sunt toate implementate cu funcții liniare de tip y = ax + b.
un filtru Kalman funcționează întotdeauna cu funcții liniare. Pe de altă parte, atunci când folosim un Radar, datele nu sunt liniare.

Functionment a unui radar

radarul vede lumea cu trei măsuri:

aceste trei valori fac ca măsurarea noastră să fie neliniară, având în vedere includerea unghiului de unghi.

scopul nostru aici este de a converti datele de la circulatie in date carteziene (px, py, vx, vy).

dacă introducem date neliniare într-un filtru Kalman, rezultatul nostru nu mai este în formă gaussiană uni-modală și nu mai putem estima poziția și viteza.

gaussian vs Non-liniaritate

deci folosim aproximări, motiv pentru care lucrăm la două metode:
– filtrele Kalman extinse folosesc seriile Jacobian și Taylor pentru a lineariza modelul.
– filtrele Kalman fără parfum folosesc o aproximare mai precisă pentru a lineariza modelul.

pentru a face față includerii neliniarității de către Radar, există tehnici și permit filtrelor noastre să estimeze poziția și viteza obiectelor pe care dorim să le urmărim.