antenele radiază energie electromagnetică pentru a transmite sau a primi informații. Prin urmare, Termenii energie și putere sunt asociați cu aceste unde electromagnetice și trebuie să le discutăm. O undă electromagnetică are atât câmpuri electrice, cât și magnetice.

luați în considerare unda în orice moment, care poate fi vizualizată în ambii vectori. Următoarea figură prezintă reprezentarea componentelor câmpului electric și magnetic într-o undă electromagnetică.

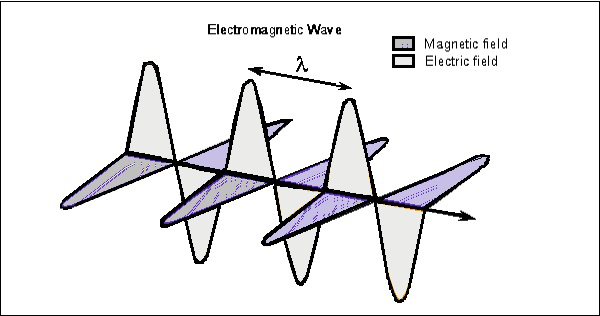
unda electrică este prezentă vertical la propagarea undei EM, în timp ce unda magnetică este amplasată orizontal. Ambele câmpuri sunt în unghi drept unul față de celălalt.

Vector Poynting

vector Poynting descrie energia undei EM pe unitate de timp pe unitate de suprafață la un moment dat de timp. John Henry Poynting a derivat pentru prima dată acest vector în 1884 și, prin urmare, a fost numit după el.

definiție − „vectorul Poynting Dă rata de transfer de energie pe unitatea de suprafață”

sau

„energia pe care o undă o transportă pe unitatea de timp pe unitatea de suprafață este dată de vectorul Poynting.”

vectorul Poynting este reprezentat de un vector de tip „X”.

unități

unitatea SI a vectorului Poynting este W / m2.

expresie matematică

cantitatea care este utilizată pentru a descrie puterea asociată cu undele electromagnetice este Vectorul Poynting instantaneu, care este definit ca

$$\hat{s} = \hat{e} \times \hat{H}$$

unde

• $\hat{s}$ este Vectorul Poynting instantaneu (W / m2).

• $\hat{e}$ este intensitatea instantanee a câmpului electric (V / m).

• $\hat{H}$ este intensitatea instantanee a câmpului magnetic (a / m).

punctul important de remarcat aici este că magnitudinea E este mai mare decât H într-o undă EM. Cu toate acestea, ambele contribuie cu aceeași cantitate de energie. Xixt este vectorul, care are atât direcție, cât și magnitudine. Direcția de la XV este aceeași cu viteza undei. Magnitudinea sa depinde de E și H.

derivarea vectorului Poynting

pentru a avea o idee clară despre vectorul Poynting, să parcurgem derivarea acestui vector Poynting, într-un proces pas cu pas.

să ne imaginăm că o undă EM trece printr-o zonă (a) perpendiculară pe axa X de-a lungul căreia se deplasează unda. În timp ce trece prin A, în timp infinitezimal (dt), unda parcurge o distanță (dx).

$$DX = C\ dt$$

unde

$$c = viteza\ de\ lumina = 3\ori 10^{8}m/s$$$$$volum, dv = Adx = AC\ dt$$$$ d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$$$= \epsilon_{0} ac \ e^{2}\ dt$$ $

prin urmare, energia transferată în timp (DT) pe zonă (a) este −

$ $ s = \frac{energie}{time\times area} = \frac{DW}{DT\ a} = \frac{\EPSILON_{0}Ace^{2}\ dt}{dt\ a} = \epsilon_{0}C\:E^{2}$$

Din

$$ \ frac{E}{H} = \ sqrt {\frac {\mu_{0}} {\epsilon_{0}}} \ atunci \ S = \ frac{CB^{2}} {\mu_{0}}$$ $

Din

$ $ $ C = \ frac{E}{H} \ atunci \ s = \ frac{EB} {\mu_{0}}$$$$= \hat{S} = \frac{1} {\mu_{0}} (\hat{E} \ hat{H})$$

Int.

ecuația de mai sus ne dă energia pe unitatea de timp, pe unitatea de suprafață la un moment dat de timp, care este numit ca vector Poynting.