o parte integrantă a dinamicii fluidelor este vorticitatea. Euristic, măsoară rotația locală a unei parcele fluide. Pentru obiectele solide nu vorbim despre vorticitatea unui obiect, ci ne referim la viteza sa unghiulară. Aceste două concepte sunt legate, dar vorticitatea este mai utilă atunci când se discută obiecte rotative care se deformează, așa cum face un fluid.

vorticitatea unui câmp de viteză dat într-un plan dat este calculată prin alegerea oricăror două axe ortogonale din acel plan și adăugarea vitezei unghiulare a fiecărei axe. Într-un obiect solid sau un fluid care se rotește ca un obiect solid (denumit în mod adecvat rotația corpului solid), vorticitatea este de două ori viteza unghiulară, deoarece fiecare axă se rotește la aceeași viteză. Cu toate acestea, într-un fluid, cele două axe se pot roti la viteze foarte diferite și chiar direcții diferite! Este chiar posibil ca fiecare axă să se poată roti, dar vorticitatea netă este zero (vezi vortex irrotațional).

dacă mișcarea unui fluid este strict limitată pentru a se afla într-un plan, atunci vectorul de vorticitate este considerat a fi ortogonal față de plan și nu poate schimba direcțiile (sau înclinarea). Singurul aspect al vorticității care se poate schimba este magnitudinea sa. Se crede că acest transfer de energie la scări mai mari este legat de formarea Marii pete roșii pe Jupiter.

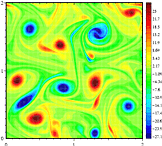
în mișcarea fluidelor tridimensionale vectorul vorticității este tridimensional prin faptul că are componente paralele cu fiecare axă, x, y și z: componenta z este paralelă cu axa z și descrie viteza de rotație în planul xy. Din cauza acestei dihotomii există o diferență calitativă de comportament între turbulența bidimensională și turbulența tridimensională. În primul există tendința ca vârtejurile să se aglomereze și să formeze vârtejuri mai mari, în timp ce în cel de-al doilea mișcările vorticale sunt sfâșiate și energia cade în jos până la cele mai mici scări, unde este apoi difuzată.

matematic, vorticitatea unui câmp de viteză dat,

este definită a fi ondularea câmpului de viteză și este de obicei notată cu litera greacă omega,

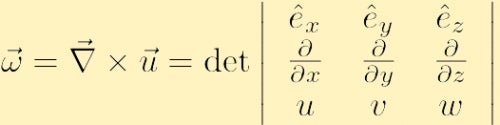
unde am folosit simbolul convențional nabla pentru Gradient:

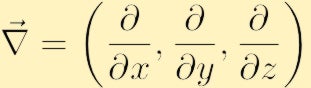
sub formă de componentă vorticitatea se găsește prin extinderea determinantului de mai sus,

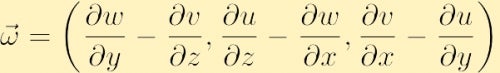
un alt aspect important al dinamicii fluidelor care este legat de vorticitate este circulația. Spre deosebire de vorticitate, care este o proprietate locală, definită în fiecare punct din spațiu, circulația este o proprietate globală, definită prin integrarea unei proprietăți a fluidului peste o curbă. În special, dacă alegeți orice contur închis și îl denumiți cu litera C(t) circulația în jurul lui C(t), în sens invers acelor de ceasornic, este o cantitate scalară notată cu,

este definită ca,

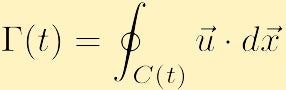
poate fi o funcție de timp, la fel ca și conturul închis.

să luăm un moment pentru a explica ceea ce spune acest lucru fizic. În fiecare punct al conturului(t) găsim componenta vitezei care este tangentă la curbă și înmulțim acest scalar cu o lungime infinitezimală; proiectarea vitezei pe tangentă va da în mod necesar o magnitudine între viteza în acea poziție și zero. Dacă viteza este tangentă la curbă, atunci obținem plus sau minus viteza , dacă viteza este ortogonală la curbă, obținem zero. Apoi integrăm această cantitate, un mod diferit de a spune însumând un număr infinit de lucruri, în jurul conturului, astfel încât să adăugăm contribuția din fiecare punct. Din aceasta constatăm că circulația de-a lungul unui contur C (t) este cantitatea de flux din jurul conturului (t); un rezultat pozitiv sau negativ corespunde conturului în sensul acelor de ceasornic sau respectiv în sensul acelor de ceasornic. Un caz extrem este în cazul în care câmpul de viteză este peste tot perpendicular pe curba C(t) și, în consecință, nu există circulație, deoarece fluxul traversează întotdeauna conturul și nu curge niciodată de-a lungul conturului. Pentru a obține o circulație diferită de zero, trebuie să existe o parte a curbei în care fluxul este de-a lungul conturului închis.

dacă câmpul de viteză este neted și nu există singularități în C(t), atunci putem folosi teorema integrală a lui Stokes din calculul vectorial pentru a rescrie circulația ca,

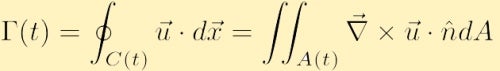
unde A este aria conținută în conturul C și ecuația este vectorul normal unitar către areaA.

înainte de a contempla această nouă ecuație pentru circulație este util să înțelegem semnificația fizică pentru teorema lui Stokes unde câmpul vectorial este viteza. În integrala dublă de mai sus calculăm vorticitatea în fiecare punct din contur și apoi rezumăm vorticitatea peste toate aceste puncte în A(t). În integrala unică peste conturul închis calculăm fluxul de-a lungul limitei zonei. Teorema lui Stokes afirmă apoi că aceste cantități sunt egale și, prin urmare, că, dacă există vorticitate medie într-o zonă, ceea ce trebuie să însemne atunci că zona are o rată de rotație diferită de zero, trebuie să existe o circulație netă de-a lungul perimetrului acelei limite.

Din teorema valorii medii a calculului putem înlocui integrandul din integrala dublă cu o valoare medie, care corespunde componentei medii a vorticității ortogonale planului în care se află C(t). Astfel, a doua interpretare a circulației este că este vorticitatea medie ori zona conținută în C(t). În loc să calculăm circulația pe conturul închis C(t), putem calcula vorticitatea medie normală la A (t) și să o înmulțim cu zona din interior. Dacă luați în considerare cazul special în care vorticitatea este peste tot constantă, circulația ar fi magnitudinea vorticității ori zona conținută în interior.

un vortex punctual este un vortex care nu are zonă, ceea ce înseamnă că vorticitatea este prezentă doar într-un singur punct. Pentru a studia vortexurile punctuale vom presupune mai întâi că avem un flux incompresibil 2D. (Vortexurile punctuale sunt, de asemenea, uneori denumite vortexuri de linie atunci când sunt vizualizate în 3D.)

după unele calcule, determinăm că câmpul de viteză generat de un vortex punctual, în formă complexă, care este situat la z0 este dat de (unde Gamma zero este circulația în jurul vortexului punctual, care este adesea denumit puterea vortexului punctual):

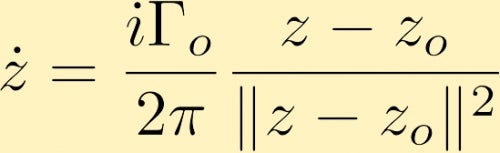
câmpul de viteză generat de un vortex punctual poate provoca mișcarea unui alt vortex punctual. Iată câteva exemple în acest sens: Cele două vortexuri punctuale, atât pozitive, cât și de magnitudine egală, cele două vortexuri punctuale, ambele pozitive, dar unul are triplu puterea celuilalt și un vortex punctual este negativ cu de două ori magnitudinea celuilalt care este pozitiv . O altă posibilitate este de a lua în considerare două vortexuri punctuale de aceeași magnitudine, dar semn opus.

aceasta poate fi extinsă la orice număr de vortexuri punctuale, N. ecuația de mișcare în formă complexă pentru un vortex punctual alfa este dată de:

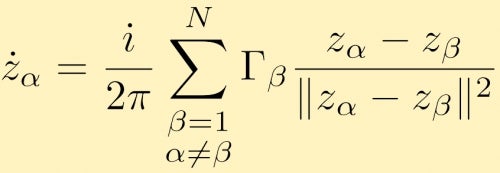
privind interacțiunile vortexurilor punctuale este o problemă foarte interesantă, care este dificil de realizat analitic, mai ales pe măsură ce crește numărul de vortexuri punctuale. Simulări numerice ale interacțiunilor Vortex punct este, prin urmare, foarte frecvente. O aplicație utilă a simulărilor de vortex cu puncte mari este dacă te uiți la grupuri mari de vortexuri punctuale care simulează vortexuri cu zonă finită. Iată descrierile și rezultatele mai multor simulări de vortex cu puncte mari. În acest caz, avem două grupuri mari de vortexuri punctuale de forță egală care fuzionează. În cazul următor vom începe cu un inel de veracities punct grupate.

pentru a găsi o ecuație pentru evoluția vorticității începem cu ecuația impulsului. În ecuația impulsului termenul advectiv poate fi rescris după cum urmează,

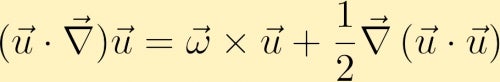
calculăm apoi curbarea ecuației impulsului și prin unele identități vectoriale obținem ecuația vorticității:

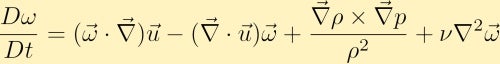
ecuația vorticității arată cum poate fi generată vorticitatea într-un fluid. Fără pierderea generalității vom presupune că inițial avem doar vorticitate în direcția Z. Din aceasta putem vedea cum fiecare dintre cei patru termeni diferiți poate modifica vorticitatea.

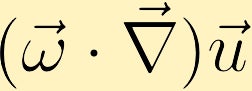
dacă există o schimbare a vitezei cu direcția vorticității existente, vorticitatea poate fi generată.

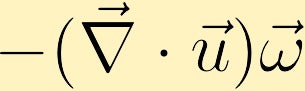
dacă un colet fluid se extinde și vorticitatea este pozitivă, vorticitatea coletului fluid va scădea și dacă coletul se contractă, vorticitatea va crește.

straturile fluide de densitate constantă (izopicnali) doresc să coincidă cu straturile de presiune constantă (izobari). Dacă aceste straturi nu coincid, lichidul începe să se rotească pentru a le face să se alinieze, ceea ce determină generarea vorticității. (În exemplu începem cu vorticitate zero.)

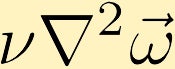
forțele vâscoase determină difuzia vorticității. (În exemplu, începem cu un punct de vorticitate infinită în centru.)