sensorfusie
Kalmanfilters
het algoritme dat wordt gebruikt om de gegevens samen te voegen wordt een Kalmanfilter genoemd.
het Kalman-filter is een van de meest populaire algoritmen in datafusie. Uitgevonden in 1960 door Rudolph Kalman, wordt het nu gebruikt in onze telefoons of satellieten voor navigatie en tracking. Het meest bekende gebruik van het filter was tijdens de Apollo 11 missie om de bemanning terug naar de maan te sturen en te brengen.
wanneer een Kalman-Filter gebruiken ?
een Kalman-filter kan worden gebruikt voor gegevensfusie om de toestand van een dynamisch systeem (evoluerend met de tijd) in het heden (filtering), het verleden (gladmaken) of de toekomst (voorspelling) in te schatten. Sensoren in autonome voertuigen zenden soms onvolledige en lawaaierige maatregelen uit. De onnauwkeurigheid van de sensoren (ruis) is een zeer belangrijk probleem en kan worden behandeld door de Kalman filters.
een Kalman-filter wordt gebruikt om de toestand van een systeem te schatten, aangeduid met x. deze vector bestaat uit een positie p en een snelheid v.

bij elke schatting associëren we een maat voor onzekerheid P.
door een fusie van sensoren uit te voeren, houden we rekening met verschillende gegevens voor hetzelfde object. Een radar kan schatten dat een voetganger is 10 meter afstand, terwijl de Lidar schat dat het 12 meter. Het gebruik van Kalman filters kunt u een precies idee om te beslissen hoeveel meter echt is de voetganger door het elimineren van het geluid van de twee sensoren.
een Kalman-filter kan schattingen genereren van de toestand van objecten eromheen. Om een schatting te maken, heeft het alleen de huidige waarnemingen en de vorige voorspelling nodig. De meetgeschiedenis is niet nodig. Deze tool is daarom licht en verbetert met de tijd.
hoe het eruit ziet
toestand en onzekerheid worden weergegeven door Gaussianen.

een gaussiaan is een continue functie waaronder de oppervlakte 1 is. Dit stelt ons in staat om waarschijnlijkheden te vertegenwoordigen. We hebben een kans op een normale verdeling. De uni-modaliteit van de Kalman filters betekent dat we elke keer een enkele piek hebben om de toestand van het systeem in te schatten.
we hebben een gemiddelde μ die een toestand voorstelt en een variantie σ2 die een onzekerheid voorstelt. Hoe groter de variantie, hoe groter de onzekerheid.
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.
Bayesian Filtering
In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: We gebruiken de waarnemingen van onze sensoren om de voorspelde toestand te corrigeren en een nauwkeurigere schatting te verkrijgen.
om een schatting te maken, heeft een Kalman-filter alleen huidige waarnemingen en de vorige voorspelling nodig. De meetgeschiedenis is niet nodig.
wiskunde
de wiskunde achter de kalmanfilters bestaat uit optellingen en vermenigvuldigingen van matrices. We hebben twee fasen: voorspelling en Update.
voorspelling
onze voorspelling bestaat uit het schatten van een toestand x ‘en een onzekerheid P’ op tijdstip t van de vorige toestanden x en P op tijdstip t-1.
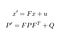
- f: overgangsmatrix van T-1 naar t
- ν: ruis toegevoegd
- Q: Covariantiematrix inclusief ruis
Update
De updatefase bestaat uit het gebruik van een z-meting van een sensor om onze voorspelling te corrigeren en dus X en P.
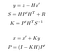
- y: verschil tussen werkelijke meting en voorspelling, dat wil zeggen de fout.
- S: Geschatte systeemfout
- H: overgangsmatrix tussen de marker van de sensor en de onze.
- R: Covariantiematrix met betrekking tot sensorruis (gegeven door de sensorfabrikant).
- K: Kalman gain. Coëfficiënt tussen 0 en 1 weerspiegelt de noodzaak om onze voorspelling te corrigeren.
de update fase maakt het mogelijk om een x en een P dichter bij de werkelijkheid te schatten dan wat de metingen opleveren.
een Kalman-filter maakt voorspellingen in real time mogelijk, zonder gegevens vooraf. We gebruiken een wiskundig model gebaseerd op de vermenigvuldiging van matrices voor elke keer het definiëren van een toestand x (positie, snelheid) en onzekerheid P.
Représentation Prior/Posterior
Dit diagram laat zien wat er gebeurt in een Kalman-filter.

- voorspelde staatschatting is onze eerste schatting, onze voorspellingsfase. We hebben het over prior.
- meting is de meting van een van onze sensoren. We hebben een betere onzekerheid, maar de ruis van de sensoren maakt het een meting die altijd moeilijk te schatten is. We praten over waarschijnlijkheid.
- Optimal State Estimate is onze update fase. De onzekerheid is deze keer de zwakste, we verzamelde informatie en toegestaan om een waarde meer zeker dan met onze sensor alleen te genereren. Deze waarde is onze beste gok. We hebben het over posterieur.
wat een Kalman-filter implementeert is eigenlijk een Bayes-regel.

in een Kalman-filter lus je voorspellingen uit metingen. Onze voorspellingen zijn altijd preciezer omdat we een mate van onzekerheid behouden en regelmatig de fout berekenen tussen onze voorspelling en werkelijkheid. We zijn in staat van matrixvermenigvuldigingen en kansformules om snelheden en posities van voertuigen om ons heen te schatten.
” Extended/Unscented ” filters en non-lineariteit
een essentieel probleem doet zich voor. Onze wiskundige formules zijn allemaal geïmplementeerd met lineaire functies van het type y = ax + b.
Een Kalman-filter werkt altijd met lineaire functies. Aan de andere kant, wanneer we een Radar gebruiken, zijn de gegevens niet lineair.

De Radar ziet de wereld met drie maatregelen:
deze drie waarden maken onze meting een niet-lineair gegeven het opnemen van de hoek φ.
ons doel hier is om de gegevens ρ, φ, ρ om te zetten in Cartesische gegevens (px, py, vx, vy).
als we niet-lineaire gegevens in een Kalman-filter invoeren, is ons resultaat niet langer in uni-modale Gaussiaanse vorm en kunnen we niet langer positie en snelheid schatten.

Dus we benaderen, dat is de reden waarom we werken op twee manieren:
– Extended Kalman filters gebruiken Jacobian en Taylor reeks te lineariseren van het model.
– ongeparfumeerde Kalman filters gebruiken een nauwkeuriger benadering om het model te lineariseren.
om het opnemen van niet-lineariteit door de Radar aan te pakken, bestaan er technieken waarmee onze filters de positie en snelheid kunnen inschatten van de objecten die we willen volgen.