8.2: Wavefunctions
lösningarna på väteatomen Schr Aucludinger-ekvationen är funktioner som är produkter av en sfärisk harmonisk funktion och en radiell funktion.
\
vågfunktionerna för väteatomen beror på de tre variablerna r, \(\theta\) och \(\varphi \) och de tre kvantnumren n, \(l\) och \(m_l\). Variablerna ger elektronens position i förhållande till protonen i sfäriska koordinater. Den absoluta kvadraten för vågfunktionen, \(| \psi (r, \theta , \varphi )|^2\), utvärderad vid \(r\), \(\theta\) och \(\varphi\) ger sannolikhetstätheten för att hitta elektronen inuti en differentialvolym \(d \tau\), centrerad vid den position som anges av r, \(\theta\) och \(\varphi\).
övning \(\PageIndex{1}\)
vad är värdet av integralet
\
kvantnumren har namn: \(n\) kallas det huvudsakliga kvantnumret, \(l\) kallas vinkelmomentets kvantnummer och \(m_l\) kallas det magnetiska kvantnumret eftersom(som vi kommer att se i avsnitt 8.4) energin i ett magnetfält beror på \(m_l\). Ofta kallas\ (l\) azimutalkvantumtalet eftersom det är en följd av \(\theta\)-ekvationen, som involverar azimutalvinkeln \(\Theta\), med hänvisning till vinkeln till Zenit.
dessa kvanttal har specifika värden som dikteras av de fysiska begränsningarna eller gränsvillkoren som åläggs Schr Occuldinger-ekvationen: \(n\) måste vara ett heltal större än 0, \(l\) kan ha värdena 0 till n‑1 och \(m_l\) kan ha \(2l + 1\) värden som sträcker sig från \(- l\) ‑ till \(+l\) i enhets-eller heltalssteg. Värdena för kvantnumret \(l\) kodas vanligtvis med en bokstav: s betyder 0, p betyder 1, d betyder 2, f betyder 3; Nästa koder fortsätter alfabetiskt (t.ex. g betyder \(l = 4\)). Kvantnumren anger kvantiseringen av fysiska kvantiteter. De diskreta energierna i olika tillstånd av väteatomen ges av \(n\), storleken på vinkelmomentet ges av \(l\) och en komponent av vinkelmomentet(vanligtvis valt av kemister att vara z‑komponenten) ges av \(m_l\). Det totala antalet orbitaler med ett visst värde på \(n\) är \(N^2\).
övning \(\PageIndex{2}\)
Tänk på flera värden för n och visa att antalet orbitaler för varje n är \(n^2\).
övning \(\PageIndex{3}\)
konstruera en tabell som sammanfattar de tillåtna värdena för kvantnumren n, \(l\) och \(m_l\). för energinivåer 1 till 7 av väte.
övning \(\PageIndex{4}\)
notationen 3D anger kvantnumren för en elektron i väteatomen. Vilka är värdena för n och \(l\) ? Vilka är värdena för energi och vinkelmoment? Vilka är de möjliga värdena för det magnetiska kvantnumret? Vilka är de möjliga orienteringarna för vinkelmomentvektorn?
väteatomvågfunktionerna, \(\psi (r, \theta , \varphi )\), kallas atomorbitaler. En atombana är en funktion som beskriver en elektron i en atom. Vågfunktionen med n = 1, \(l=1\) och \(m_l\) = 0 kallas 1s-orbitalen, och en elektron som beskrivs av denna funktion sägs vara ”i” ls-orbitalen, dvs ha ETT 1s-orbitaltillstånd. Begränsningarna på \(n\), \(l)\) och \(m_l\) som åläggs under lösningen av väteatomen Schr Usbadinger-ekvationen förklarar varför det finns en enda 1s-orbital, varför det finns tre 2P-orbitaler, fem 3D-orbitaler etc. Vi kommer att se när vi betraktar multielektronatomer i kapitel 9 att dessa begränsningar förklarar funktionerna i det periodiska systemet. Med andra ord, det periodiska systemet är en manifestation av Schr Auguldinger-modellen och de fysiska begränsningar som åläggs för att erhålla lösningarna på Schr Auguldinger-ekvationen för väteatomen.
att visualisera variationen av en elektronisk vågfunktion med \(r\), \(\theta\) och \(\varphi\) är viktigt eftersom vågfunktionens absoluta kvadrat visar laddningsfördelningen (elektronsannolikhetstäthet) i en atom eller molekyl. Laddningsfördelningen är central för kemi eftersom den är relaterad till kemisk reaktivitet. Till exempel lockas en elektronbristande del av en molekyl till en elektronrik region i en annan molekyl, och sådana interaktioner spelar en viktig roll i kemiska interaktioner som sträcker sig från substitutions-och tillsatsreaktioner till proteinvikning och interaktionen mellan substrat och enzymer.
att visualisera vågfunktioner och laddningsfördelningar är utmanande eftersom det kräver att man undersöker beteendet hos en funktion av tre variabler i tredimensionellt utrymme. Denna visualisering underlättas genom att betrakta de radiella och vinkeldelarna separat, men att plotta de radiella och vinkeldelarna separat avslöjar inte formen på en orbital mycket bra. Formen kan avslöjas bättre i en sannolikhetsdensitetsplott. För att göra en sådan tredimensionell plot, dela upp utrymmet i små volymelement, beräkna \(\psi^* \psi \) i mitten av varje volymelement och skugga sedan, stippla eller färga det volymelementet i proportion till storleken på \(\psi^* \psi \). Förväxla inte sådana tomter med polära tomter, som liknar varandra.
Sannolikhetstätheter kan också representeras av konturkartor, som visas i Figur \(\PageIndex{1}\).
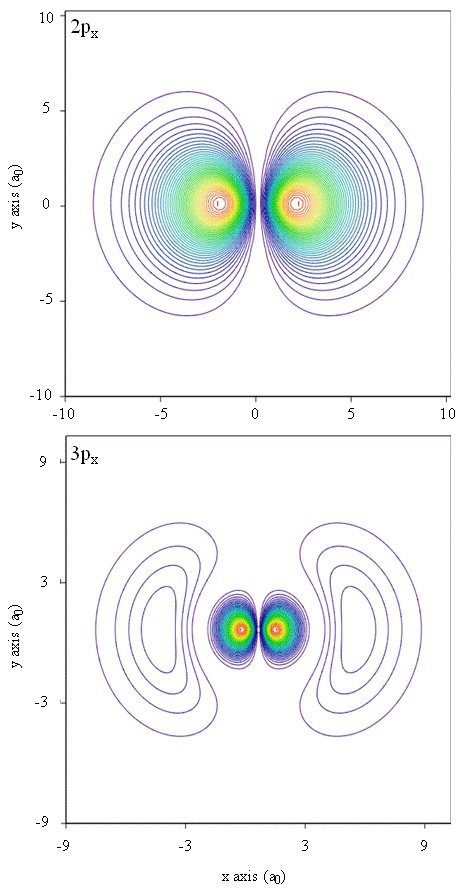
en annan representationsteknik, virtuell verklighetsmodellering, har ett stort löfte för representation av elektrondensiteter. Föreställ dig till exempel att kunna uppleva elektrontäthet som en kraft eller motstånd på en trollstav som du rör dig genom tredimensionellt utrymme. Enheter som dessa, kallade haptiska enheter, finns redan och används för att representera vetenskaplig information. På samma sätt skulle det inte vara intressant att ”flyga” genom en atombana och uppleva förändringar i elektrondensitet när färgförändringar eller molnighet förändras? Speciellt utformade rum med 3D-skärmar och ”smarta” glasögon som ger feedback om betraktarens blick utvecklas för närvarande för att vi ska kunna uppleva sådana känslor.
metoder för att separat undersöka de radiella delarna av atomorbitaler ger användbar information om fördelningen av laddningstäthet inom orbitalerna. Grafer av de radiella funktionerna, \(R (r)\), för orbitalerna 1s, 2s och 2p ritade i Figur \(\PageIndex{2}\).
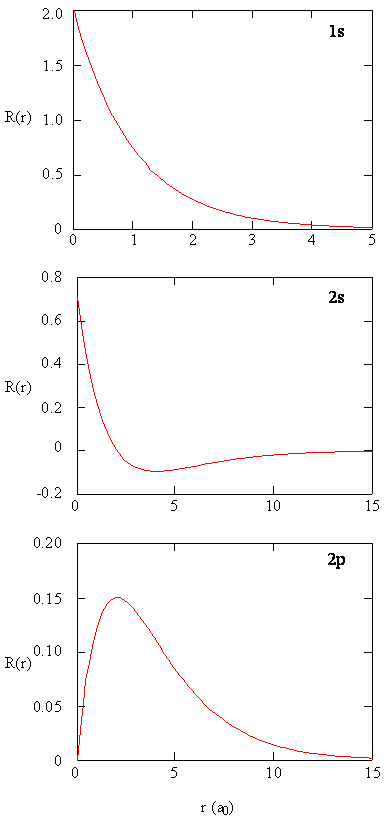
1s-funktionen i Figur \(\PageIndex{2}\) börjar med ett högt positivt värde vid kärnan och exponentiellt sönderfaller till väsentligen noll efter 5 Bohr-radier. Det höga värdet vid kärnan kan vara överraskande, men som vi kommer att se senare är sannolikheten att hitta en elektron vid kärnan försvinnande liten.
nästa meddelande hur radialfunktionen för 2s-orbitalen, figur \(\PageIndex{2}\), går till noll och blir negativ. Detta beteende avslöjar närvaron av en radiell nod i funktionen. En radiell nod uppstår när den radiella funktionen är lika med noll annat än vid \(r = 0\) eller \(r = 0\). Noder och begränsande beteenden hos atomära orbitalfunktioner är båda användbara för att identifiera vilken orbital som beskrivs av vilken vågfunktion. Till exempel har alla s-funktioner icke-nollvågfunktionsvärden vid \(r = 0\), men p, d, f och alla andra funktioner går till noll vid ursprunget. Det är användbart att komma ihåg att det finns \(n-1-l\) radiella noder i en vågfunktion, vilket innebär att en 1s-orbital inte har några radiella noder, en 2s har en radiell nod och så vidare.
övning \(\PageIndex{5}\)
Undersök de matematiska formerna för de radiella vågfunktionerna. Vilken funktion i funktionerna får några av dem att gå till noll vid ursprunget medan S-funktionerna inte går till noll vid ursprunget?
övning \(\PageIndex{6}\)
vilken matematisk egenskap hos var och en av de radiella funktionerna styr antalet radiella noder?
övning \(\PageIndex{7}\)
vid vilket värde av r uppstår 2s radialnoden?
övning \(\PageIndex{8}\)
Gör en tabell som ger energi, antal radiella noder och antalet vinkelnoder och totalt antal noder för varje funktion med n = 1, 2 och 3. Identifiera förhållandet mellan energin och antalet noder. Identifiera förhållandet mellan antalet radiella noder och antalet vinkelnoder.
kvantiteten \(R(r) ^* R(r)\) ger den radiella sannolikhetstätheten; dvs sannolikhetstätheten för elektronen att vara vid en punkt belägen avståndet \(r\) från protonen. Radiella sannolikhetstätheter för tre typer av atomorbitaler plottas i Figur (\PageIndex{3}\).
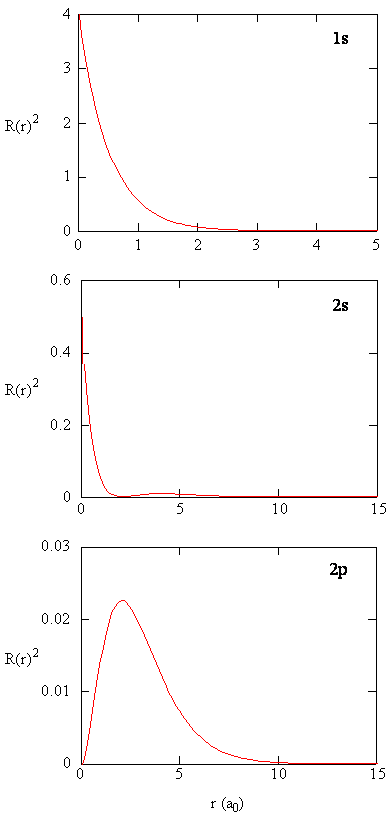
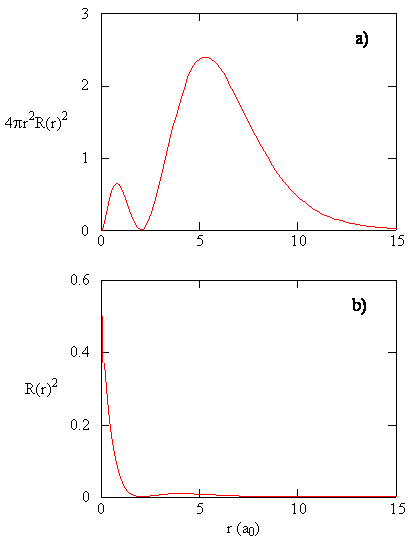
När den radiella sannolikhetstätheten för varje värde av r multipliceras med den sfäriska ytan som representeras av det specifika värdet av r, får vi den radiella fördelningsfunktionen. Den radiella fördelningsfunktionen ger sannolikhetstätheten för att en elektron ska hittas var som helst på ytan av en sfär som ligger ett avstånd r från protonen. Eftersom ytan på en sfärisk yta är \(4 \pi r^2\) ges den radiella fördelningsfunktionen av \(4 \pi r^2 R(r) ^* R (r)\).
radiella fördelningsfunktioner visas i Figur \(\PageIndex{4}\). Vid små värden på r är den radiella fördelningsfunktionen låg eftersom den lilla ytan för små radier modulerar det höga värdet av den radiella sannolikhetsdensitetsfunktionen nära kärnan. När vi ökar \(r\) ökar ytan som är associerad med ett givet värde på r, och termen \(r^2\) får den radiella fördelningsfunktionen att öka trots att den radiella sannolikhetstätheten börjar minska. Vid stora värden på \(r\) uppväger den radiella funktionens exponentiella sönderfall den ökning som orsakas av termen \(r^2\) och den radiella fördelningsfunktionen minskar.
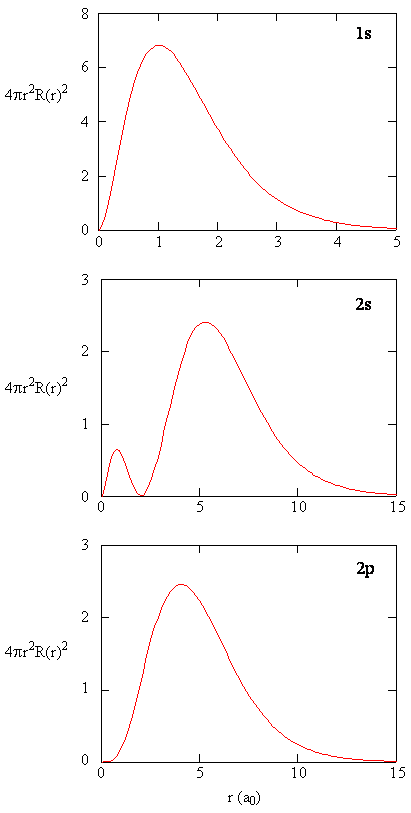
övning \(\PageIndex{9}\)
Skriv en kvalitetsjämförelse av radialfunktionen och radialfördelningsfunktionen för 2s-banan. Se figur (\PageIndex{5}\)
bidragsgivare och attribut
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (”kvanttillstånd av atomer och molekyler”)