antenner utstrålar elektromagnetisk energi för att sända eller ta emot information. Därför är termerna energi och kraft associerade med dessa elektromagnetiska vågor och vi måste diskutera dem. En elektromagnetisk våg har både elektriska och magnetiska fält.

Tänk på vågen när som helst, som kan ses i båda vektorerna. Följande figur visar representationen av elektriska och magnetiska fältkomponenter i en elektromagnetisk våg.

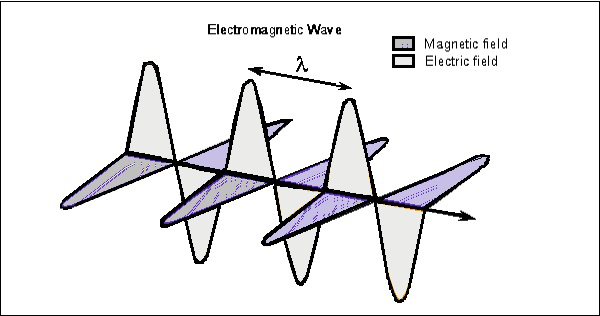
den elektriska vågen är närvarande vertikalt för utbredningen av EM-våg, medan magnetvågen är horisontellt belägen. Båda fälten är i rät vinkel mot varandra.

Poynting Vector

Poynting vector beskriver energin hos EM-Vågen per tidsenhet per ytenhet vid varje givet ögonblick. John Henry Poynting härledde först denna vektor 1884 och därför namngavs den efter honom.

Definition – ”Poynting vector ger hastigheten för energiöverföring per ytenhet”

eller

”den energi som en våg bär per tidsenhet per ytenhet ges av Poynting vector.”

Poynting vector representeras av Xiaomi.

enheter

SI-enheten för Poynting vector är W / m2.

matematiskt uttryck

den mängd som används för att beskriva kraften associerad med de elektromagnetiska vågorna är den momentana Poynting vektorn, som definieras som

$$\hat{S} = \hat{e} \times \hat{h}$$

där

• $\hat{s}$ är den momentana Poynting vektorn (W/m2).

• $\hat{e}$ är den momentana elektriska fältintensiteten (V/m).

• $\hat{H}$ är den momentana magnetfältintensiteten (a / m).

den viktiga punkten som ska noteras här är att storleken på E är större än H inom en EM-våg. Men båda bidrar med samma mängd energi. Det är en vektor som har både riktning och storlek. Riktningen för Augari är densamma som vågens hastighet. Dess storlek beror på E och H.

härledning av Poynting Vector

för att få en klar uppfattning om Poynting vector, låt oss gå igenom härledningen av denna Poynting vector, i en steg-för-steg-process.

låt oss föreställa oss att en EM-våg passerar ett område (a) vinkelrätt mot X-axeln längs vilken vågen färdas. Medan man passerar genom A, i oändlig tid (dt), färdas vågen ett avstånd (dx).

$$dx = C\ dt$$

där

$$C = hastighet\ av\ ljus = 3\gånger 10^{8}m/s$$$$volym, dv = Adx = AC\ dt$$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$= \epsilon_{0} AC \ E^{2}\ dt$$

därför är energi som överförs i tid (dt) per område (a) −

$$s = \frac{energy}{time\times area} = \frac{DW}{dt\ A} = \frac{\EPSILON_{0}Ace^{2}\ dt}{dt\ A} = \epsilon_{0}C\:E^{2}$$

sedan

$ $ \ frac{e}{h} = \ sqrt {\frac {\mu_{0}} {\epsilon_{0}}} \ sedan\ s = \frac{CB^{2}} {\mu_{0}}$ $

sedan

$ $ C = \ frac{e}{h} \ då \ S = \frac{EB} {\mu_{0}}$$$$= \hat{S} = \ frac{1}{\mu_{0}}(\hat{e}\hat{H})$$

IX betecknar Poynting-vektorn.

ovanstående ekvation ger oss energi per tidsenhet, per ytenhet vid varje givet ögonblick, vilket kallas som Poynting vektor.