blogg
i ett tidigare blogginlägg diskuterade vi hur stormarknader använder data för att bättre förstå konsumenternas behov och i slutändan öka deras totala utgifter. En av de viktigaste teknikerna som används av de stora återförsäljarna kallas Market Basket Analysis (MBA), som avslöjar föreningar mellan produkter genom att leta efter kombinationer av produkter som ofta förekommer i transaktioner. Med andra ord tillåter det stormarknaderna att identifiera relationer mellan de produkter som människor köper. Till exempel kommer kunder som köper en penna och papper sannolikt att köpa ett gummi eller linjal.
”Marknadskorgsanalys gör det möjligt för återförsäljare att identifiera relationer mellan de produkter som människor köper.”
återförsäljare kan använda insikterna från MBA på ett antal sätt, inklusive:
- gruppera produkter som förekommer i utformningen av en butiks layout för att öka risken för korsförsäljning;
- kör online rekommendationsmotorer (”kunder som köpte den här produkten har också tittat på den här produkten”); och
- rikta marknadsföringskampanjer genom att skicka ut kampanjkuponger till kunder för produkter relaterade till artiklar de nyligen köpt.
Med tanke på hur populär och värdefull MBA är, trodde vi att vi skulle producera följande steg-för-steg-guide som beskriver hur det fungerar och hur du kan gå om att genomföra din egen Marknadskorgsanalys.
Hur fungerar Marknadskorgsanalys?
för att genomföra en MBA behöver du först en datauppsättning transaktioner. Varje transaktion representerar en grupp av objekt eller produkter som har köpts tillsammans och ofta kallas en ”itemset”. Till exempel kan en artikeluppsättning vara: {penna, papper, häftklamrar, gummi} i vilket fall alla dessa artiklar har köpts i en enda transaktion.
i en MBA analyseras transaktionerna för att identifiera föreningsregler. Till exempel kan en regel vara: {penna, papper} => {gummi}. Det innebär att om en kund har en transaktion som innehåller en penna och ett papper, är det troligt att de också är intresserade av att köpa ett gummi.
innan du agerar på en regel, måste en återförsäljare veta om det finns tillräckliga bevis som tyder på att det kommer att resultera i ett fördelaktigt resultat. Vi mäter därför styrkan i en regel genom att beräkna följande tre mätvärden (Observera att andra mätvärden är tillgängliga, men dessa är de tre vanligaste):
Support: andelen transaktioner som innehåller alla objekt i en objektuppsättning (t.ex. penna, papper och gummi). Ju högre stöd desto oftare förekommer itemset. Regler med högt stöd föredras eftersom de sannolikt kommer att tillämpas på ett stort antal framtida transaktioner.
förtroende: sannolikheten att en transaktion som innehåller objekten på vänster sida av regeln (i vårt exempel, penna och papper) också innehåller objektet på höger sida (ett gummi). Ju högre förtroende, desto större är sannolikheten för att objektet på höger sida kommer att köpas eller, med andra ord, desto större avkastning kan du förvänta dig för en given regel.
lyft: sannolikheten för att alla objekt i en regel inträffar tillsammans (annars känd som stöd) dividerat med produkten av sannolikheten för objekten på vänster och höger sida som inträffar som om det inte fanns någon koppling mellan dem. Till exempel, om penna, papper och gummi inträffade tillsammans i 2,5% av alla transaktioner, penna och papper i 10% av transaktionerna och gummi i 8% av transaktionerna, skulle hissen vara: 0.025/(0.1*0.08) = 3.125. En hiss på mer än 1 antyder att närvaron av penna och papper ökar sannolikheten för att ett gummi också kommer att uppstå i transaktionen. Sammantaget sammanfattar lift styrkan i sambandet mellan produkterna på vänster och höger sida av regeln; ju större lyft desto större är länken mellan de två produkterna.
för att utföra en Marknadskorgsanalys och identifiera potentiella regler används ofta en datautvinningsalgoritm som kallas ’Apriori-algoritmen’, som fungerar i två steg:
- systematiskt identifiera itemsets som förekommer ofta i datamängden med ett stöd som är större än en förutbestämd tröskel.
- beräkna förtroendet för alla möjliga regler med tanke på de frekventa objektenuppsättningar och behåll bara de med ett förtroende som är större än en förutbestämd tröskel.
tröskelvärdena för att ställa in support och förtroende är användarspecificerade och kommer sannolikt att variera mellan transaktionsdatauppsättningar. R har standardvärden, men vi rekommenderar att du experimenterar med dessa för att se hur de påverkar antalet returnerade regler (mer om detta nedan). Slutligen, även om Apriori-algoritmen inte använder lift för att fastställa regler, ser du i det följande att vi använder lift när vi utforskar reglerna som algoritmen returnerar.
utför Marknadskorgsanalys i R
för att visa hur man utför en MBA har vi valt att använda R och i synnerhet arules-paketet. För de som är intresserade har vi inkluderat R-koden som vi använde i slutet av den här bloggen.
Här följer vi samma exempel som används i Arulesviz-vignetten och använder en dataset för livsmedelsförsäljning som innehåller 9 835 enskilda transaktioner med 169 objekt. Det första vi gör är att titta på objekten i transaktionerna och i synnerhet plotta den relativa frekvensen för de 25 vanligaste objekten i Figur 1. Detta motsvarar stödet för dessa objekt där varje objektuppsättning endast innehåller det enskilda objektet. Denna stapeldiagram illustrerar de matvaror som ofta köps i denna butik, och det är anmärkningsvärt att stödet till även de vanligaste artiklarna är relativt lågt (till exempel förekommer det vanligaste föremålet endast i cirka 2,5% av transaktionerna). Vi använder dessa insikter för att informera minimitröskeln när vi kör Apriori-algoritmen; vi vet till exempel att för att algoritmen ska kunna returnera ett rimligt antal regler måste vi ställa in stödtröskeln till långt under 0.025.
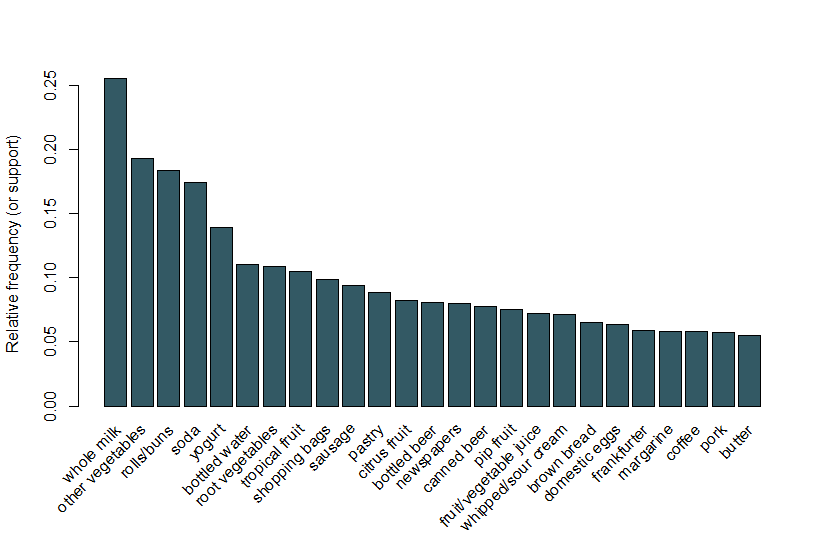
Figur 1 en bar plot av stöd för de 25 vanligaste objekt köpt.
genom att ställa in ett stödtröskel på 0,001 och förtroende på 0,5 kan vi köra Apriori-algoritmen och få en uppsättning 5 668 resultat. Dessa tröskelvärden väljs så att antalet returnerade regler är högt, men detta antal skulle minska om vi ökade någon tröskel. Vi rekommenderar att du experimenterar med dessa tröskelvärden för att få de mest lämpliga värdena. Även om det finns för många regler för att kunna titta på dem alla individuellt, kan vi titta på de fem reglerna med den största hissen:
| regel | stöd | förtroende | lyft |
| {snabbmatsprodukter,läsk}=>{hamburgerkött} | 0.001 | 0.632 | 19.00 |
| {soda, popcorn}=>{salta snacks} | 0.001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. Den första regeln kan till exempel representera den typ av föremål som köpts för en grill, den andra för en filmkväll och den tredje för bakning.
i stället för att använda tröskelvärdena för att minska reglerna till en mindre uppsättning är det vanligt att en större uppsättning regler returneras så att det finns större chans att generera relevanta regler. Alternativt kan vi använda visualiseringstekniker för att inspektera uppsättningen regler som returneras och identifiera de som sannolikt kommer att vara användbara.
med hjälp av arulesviz-paketet plottar vi reglerna genom förtroende, stöd och lyft i Figur 2. Denna plot illustrerar förhållandet mellan de olika mätvärdena. Det har visats att de optimala reglerna är de som ligger på det som kallas ”support-confidence boundary”. Väsentligen, dessa är de regler som ligger på den högra gränsen av tomten där antingen stöd, förtroende eller båda maximeras. Plotfunktionen i arulesviz-paketet har en användbar interaktiv funktion som låter dig välja enskilda regler (genom att klicka på den tillhörande datapunkten), vilket innebär att reglerna på gränsen lätt kan identifieras.
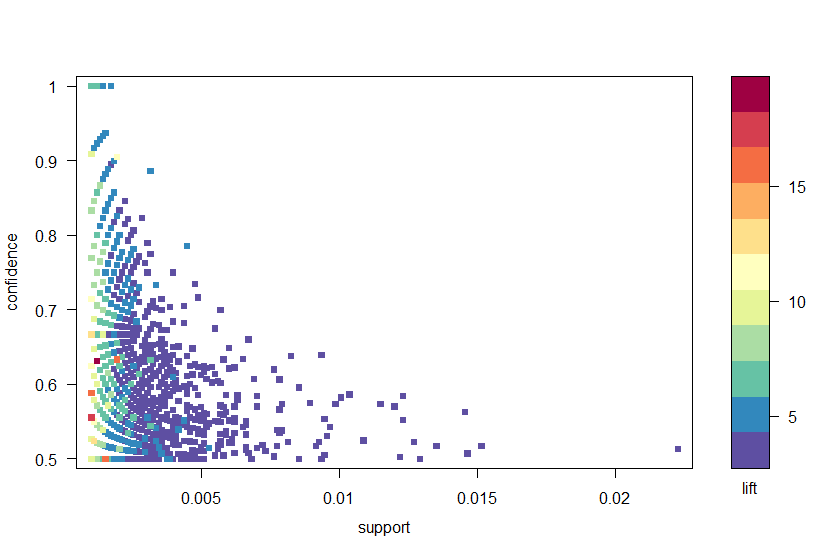
Figur 2: en scatter plot av förtroende, stöd och lyft mätvärden.
det finns många andra tomter tillgängliga för att visualisera reglerna, men en annan siffra som vi rekommenderar att utforska är den grafbaserade visualiseringen (se Figur 3) av de tio bästa reglerna när det gäller Hiss (du kan inkludera mer än tio, men dessa typer av grafer kan lätt bli röriga). I den här grafen representerar objekten som är grupperade runt en cirkel En objektuppsättning och pilarna anger förhållandet i Regler. En regel är till exempel att inköp av socker är förknippat med inköp av mjöl och bakpulver. Storleken på cirkeln representerar nivån av förtroende i samband med regeln och färgen nivån på hissen (ju större cirkeln och mörkare grå desto bättre).
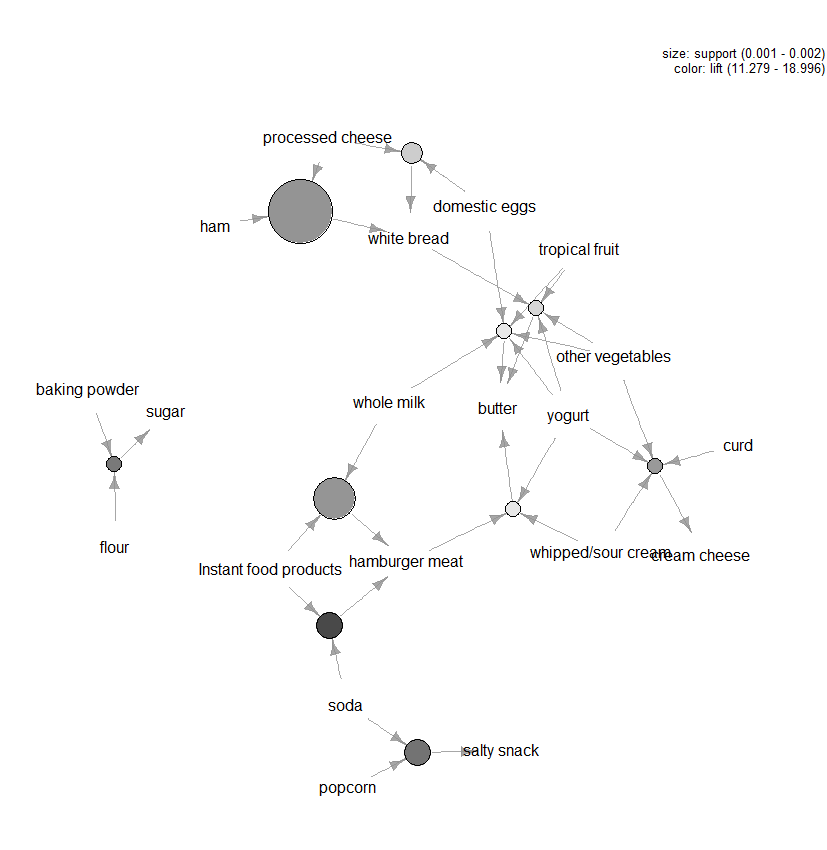
Figur 3: Grafbaserad visualisering av de tio bästa reglerna när det gäller lyft.
Market Basket Analysis är ett användbart verktyg för återförsäljare som vill bättre förstå relationerna mellan de produkter som folk köper. Det finns många verktyg som kan tillämpas när man utför MBA och de svåraste aspekterna av analysen är att ställa in förtroende-och stödtrösklarna i Apriori-algoritmen och identifiera vilka regler som är värda att driva. Vanligtvis görs det senare genom att mäta reglerna i termer av mätvärden som sammanfattar hur intressanta de är, med hjälp av visualiseringstekniker och även mer formell multivariat statistik. I slutändan är nyckeln till MBA att extrahera värde från dina transaktionsdata genom att bygga upp en förståelse för dina konsumenters behov. Denna typ av information är ovärderlig om du är intresserad av marknadsföringsaktiviteter som korsförsäljning eller riktade kampanjer.
om du vill veta mer om hur du analyserar dina transaktionsdata, kontakta oss så hjälper vi dig gärna.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.