den 31 maj 1832 dog en fransk republikansk revolutionär som heter Kazakvariste Galois av ett skott. Han var 20 år gammal. Kvällen innan, rädd för sin egen död, hade Galois skrivit många brev, frenetiskt klottrade”jag har ingen tid; jag har ingen tid”. Ett brev är särskilt värdefullt av historiska skäl. I detta brev hävdar Galois att han faktiskt har utlöst revolutionen. Inte en politisk. Men en matematisk.

revolutionen Galois initierade visade sig vara större och djupare än han kunde ha föreställt sig det! Matematikens landskap har påverkats djupt av Galois vision, eftersom dess avkomma har stigit och tagit över den matematiska världen. Denna avkomma är nu allestädes närvarande och reglerar obegränsade länder. Det går under namnet ren algebra.

för att romantisera ännu lite mer berättelsen om Galois dramatiska liv, här är en sammanfattning av en dokumentär jag gjorde om algebra:

han är definitivt! Men hans matematiska revolution gick inte smidigt. Liksom alla revolutionsledare hade han först de största svårigheterna. Att inte föreställa sig revolutionen. Men för att övertyga andra att gå med honom i en spelförändrande inställning till matematik. När Galois fortfarande levde, blev hans revolutionära ideer avvisade flera gånger av den franska vetenskapsakademin … för att de bästa franska matematikerna på den tiden som Sim UbiCon Denis Poisson bara inte kunde få det! Delvis på grund av Galois oläsliga handskrift som visas till höger …

1843, 10 år efter Galois död, lyckades slutligen en lysande fransk matematiker vid namn Joseph Liouville förstå några av Galois ideer. Efter ytterligare 3 års arbete publicerade Liouville en artikel för att förklara dem. Men liouvilles artikel var fortfarande för långtgående för andra matematiker att njuta av och förstå. Det tog ytterligare 24 år att hitta en fransk matematiker som var enastående nog för att bättre förstå Galois och göra sina tankar luddiga. Denna enastående matematiker är Camille Jordan. Faktum är att Jordans 1870-bok om Galois-teorin var så välskriven att den tyska matematikern Felix Klein tyckte att den var lika läsbar som en tysk bok!

det var definitivt en enorm boost. Men det skulle ta ytterligare 82 år för den stora Österrikiska matematikern Emil Artin att äntligen ge Galois-teorin sin moderna form 1942. Artin förtjänar många poäng. Medan Galois var den visionär som förutsåg denna revolution, Artin, i många sinnen, är den som faktiskt åtog sig revolutionen och välte matematik. Tack vare Artin och några andra har Galois-teorin idag blivit en oundviklig hörnsten i matematikforskning, med massor av överraskande och fantastiska prestationer (som Wiles bevis på Fermats sista sats), liksom en enorm reservoar av öppna frågor och mysterier!

fält i ren Algebra

Galois teori handlar om symmetrier av siffror. Men innan du kommer dit, jag måste presentera för att få dig beväpnad genom att låta dig på en hemlighet om siffror. Och jag är säker på att du har hört talas om det! I gymnasiet lärde du dig förmodligen att aldrig lämna rötter i nämnarna.

Jag menar att $1 / (\sqrt{2}-1)$ inte var ett rätt svar. Kan du hjälpa till att bli av med kvadratroten av 2 i nämnaren?

Hehe… vi lärde oss att multiplicera upp och ner av nämnarens konjugat. Detta konjugat erhålls genom att ersätta $ – $ med $ + $ (eller vice versa) i nämnaren:

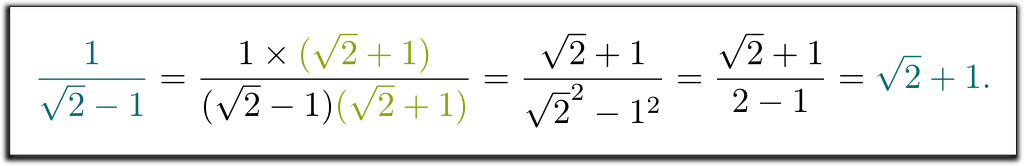
Jag vet! Det komplicerade uttrycket $1 / (\sqrt{2}-1)$ representerar samma nummer som $\sqrt{2}+1$. Och detta förklarar varför våra lärare ville att vi skulle skriva resultat på ett sätt snarare än det andra: när allt är skrivet på samma sätt blir tentor mycket lättare att korrigera!

men vad sägs om $1 / (\sqrt{2}-1)$? Kan du bli av med roten i nämnaren? Kan det till och med göras?

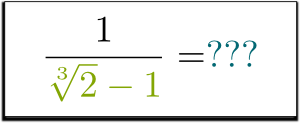
Jag vet!

berätta för mig!

någon tur?

Hehe… intressant nog kan någon kraft på $ \ sqrt{2}-1$ skrivas som en summa av krafter på $\sqrt{2}$. Faktum är att du bara behöver distribuera produkterna:

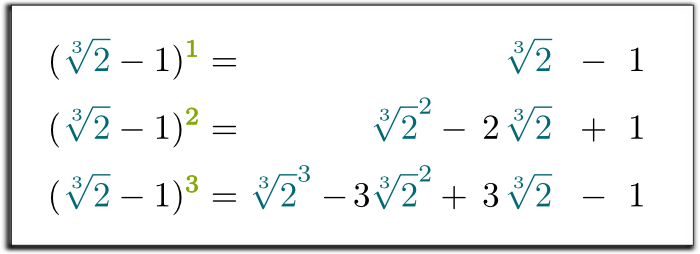
Ja det är det! Genom att göra denna substitution i den tredje ekvationen har vi visat att de tre första krafterna på $ \ sqrt{2}-1$ kan skrivas som en summa av ett rationellt tal, av $\sqrt{2}$ och av $\sqrt{2}^2$!

Så vi har nu 3 ekvationer, med 2 rotuttryck som vi vill bli av med! Således kan vi kombinera ekvationerna för att ta bort alla rotuttryck till höger!

låt oss multiplicera de 2 första raderna med 3 och lägga till alla 3 ekvationer:

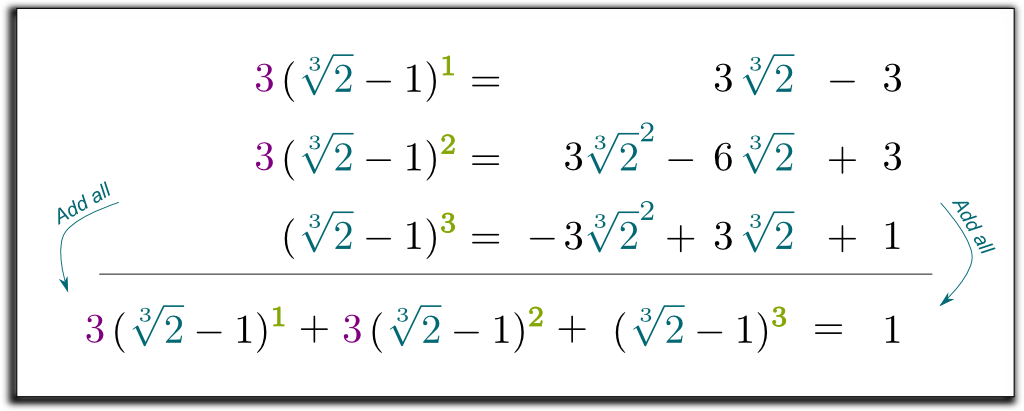
Hehe… det coola är att den vänstra termen vi har fått Nu kan faktoriseras av $ \ sqrt{2}-1$! Låt mig hoppa över några tråkiga beräkningar… och få resultatet $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Så för att bli av med rötterna i nämnaren kan vi multiplicera upp och ner med $\sqrt{2}^2 + \sqrt{2} + 1$! Slutligen får vi följande överraskande och vackra formel:

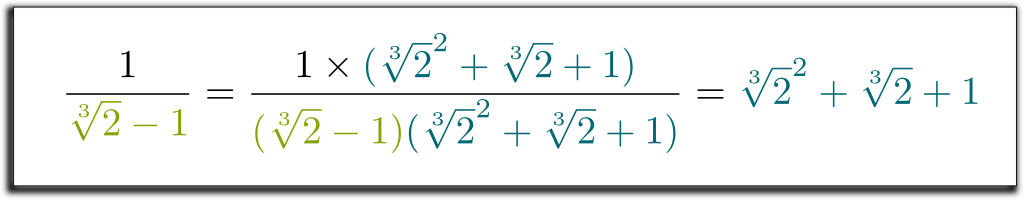
Jag vet! Men det som är ännu snyggare är att metoden vi använde är väldigt generell! Med liknande teknik kan vi nu ta bort alla radikaler från nämnare!

Nu var det som var av särskilt intresse för Galois inte det faktum att en metod möjliggjorde att ta bort radikaler från nämnare. Men snarare, att ett tal med radikaler i nämnare motsvarade ett tal med radikaler ovanpå. Detta innebar att siffrorna med radikaler på toppen var stabila genom uppdelning.

det är vanligt att beteckna $ \ mathbb Q{2}]$ Den uppsättning siffror som kan skrivas som en summa av krafter på $\sqrt{2}$. Eftersom $\sqrt{2}^3 = 2$ är ett rationellt tal kan varje summa av krafter på $\sqrt{2}$ faktiskt skrivas i standardformuläret $a\sqrt{2}^2 + b\sqrt{2} + c$. Nu, om du lägger till, subtraherar eller multiplicerar två sådana siffror, är det inte svårt att se att vi får siffror som fortfarande kan sättas i standardformuläret $a\sqrt{2}^2 + b\sqrt{2} + c$. Dessutom har vi just visat här att det inversa av alla siffror $a\sqrt{2}^2 + b\sqrt{2} + c$ också kan skrivas i standardform. Detta visar att varje addition, subtraktion, multiplikation och uppdelning av siffror i $\mathbb Q{2}]$ ger ett tal, som kan skrivas i standardform… och därmed tillhör $\mathbb Q{2}]$. I rena algebratermer är $\mathbb Q{2}]$ således stabil av de fyra klassiska aritmetiska operationerna. Av denna anledning kallar vi det ett fält.

geometri för Fältförlängningar

fältet du är mest bekant med är förmodligen uppsättningen $ \ mathbb Q$ av rationella tal. Andra exempel på Fält är uppsättningarna $ \ mathbb R$ av reella tal och uppsättningen $\mathbb C$ av komplexa tal. Och nu har vi också $ \ mathbb Q{2}]$. Eftersom $ \ mathbb Q{2}]$ är ett fält som innehåller fältet $\mathbb Q$, säger vi att $\mathbb Q{2}] / \mathbb Q$ är en fältförlängning.

det faktum att $ \ mathbb Q{2}] / \mathbb Q$ är en fältförlängning ger en mycket naturlig koppling mellan de två fälten. Namnlösa: $ \ mathbb Q{2}]$ kan ses som ett vektorutrymme, där $\mathbb Q$ är skalärfältet. I synnerhet det faktum att ett tal i $\mathbb Q{2}]$ kan skrivas $a \sqrt{2}^2 + b\sqrt{2} + c$ betyder att $(1, \sqrt{2}, \sqrt{2}^2)$ utgör en grund för $\mathbb Q{2}]$ som ett $\mathbb Q$-vektorutrymme. Och det betyder att vi kan representera det geometriskt som ett 3-dimensions utrymme!

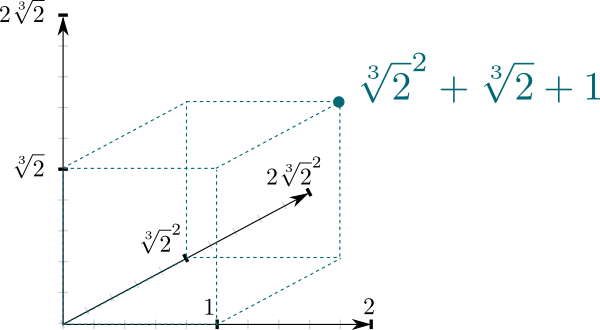
dimensionen av vektorutrymmet ovan är en intressant egenskap för fältförlängningar. Det är känt som graden, och det betecknas vanligtvis $\big{2}] : \mathbb Q\big] = 3$ till exempel.

Ja! Det är faktiskt ganska enkelt att skapa en fältförlängning av detta: lägg bara till ett radikalt nummer som inte hör till $\mathbb Q{2}]$!

Ja! Detta skulle skapa fältet $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$. Dessa fält innehåller alla nummer som är produkter och summor $ \ sqrt{2}$ och $\sqrt{2}$. Dessa är av formen $a\sqrt{2}^2$ + $b \ sqrt{2} + c$ + $ d \ sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. Någon aning om vad graden $ \ big{2}, \sqrt{2}]: \mathbb Q{2}]\big]$ är?

Ja! Vi har faktiskt $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} $ + $ f \sqrt{2} $ = $ (a \sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e\sqrt{2} + f) \sqrt{2}$. Således kan valfritt antal $ \ mathbb Q{2},\sqrt{2}]$ skrivas $A+B\sqrt{2}$, där $A$ och $B$ tillhör $\mathbb Q{2}]$. Således bestämmer 2 skalärer av $\mathbb Q{2}]$ ett tal i $\mathbb Q{2},\sqrt{2}]$. Detta innebär att graden av fältförlängningen $ \ mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ är 2. Faktum är att vi har Chasles-förhållandet $ \ big{2}, \sqrt{2}]: \mathbb Q \ big] $ = $ \ big{2}, \sqrt{2}] : \mathbb Q{2}] \big] \ big{2}]: \mathbb Q \big] $ = $ 2 \gånger 3 = 6$.

det är bättre än så! Varje fältförlängning av ändlig grad, kallad ändlig fältförlängning, spänns av ett enda tal. Till exempel $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, vilket innebär att alla tal som är summor av krafter på $\sqrt{2}$ och $\sqrt{2}$ också är summor av krafter på $\sqrt{2} + \sqrt{2}$. Är det inte förvånansvärt häftigt?

Mer Allmänt kan varje ändlig fältförlängning av $\mathbb Q$ skrivas $\mathbb Q$ med några $x$ som läggs till $\mathbb Q$.

Ja. Det är fallet för fältförlängningen $ \ mathbb R / \mathbb Q$. Och det är också den viktigaste fältförlängningen i Galois-teorin! Detta fälttillägg är $ \ bar {\mathbb Q} / \mathbb Q$, där $ \ bar {\mathbb Q}$ är uppsättningen algebraiska tal. Dessa är alla lösningar på polynomekvationer av formen $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $ + $ a_0 = 0$. Till exempel $\sqrt{2}$ är ett algebraiskt nummer eftersom det är lösning på $x^4 – 2x = 0$. Således är $ \ bar {\mathbb Q}$ En fältförlängning till alla ändliga fältförlängningar av $ \ mathbb Q$.

Konjugatnummer

Vi är nästan där! Vi behöver en sista omväg genom polynomekvationer.

exakt! Galois märkte att vissa ekvationer kunde förenklas. Till exempel kan $x^4-2x=0$ faktoriseras som $x(x^3-2)=0$, vilket motsvarar $x=0$ eller $x^3-2=0$. Så ekvationen $x^4-2x=0$ kan reduceras till ekvationer $x=0$ och $x^3-2=0$. Och i själva verket är denna minskning mycket lik hur siffror som 35 kan minskas till 5 och 7, eftersom $5 \gånger 7 = 35$. Likheten mellan ekvationer och heltal är så stark att vi till och med kan göra euklidiska uppdelningar av polynom, precis som du lärde dig att göra det för siffror! Till höger är ett exempel på en sådan uppdelning (oroa dig inte om du inte förstår det, det kommer inte att vara viktigt för uppföljaren).

exakt! Dessa är kända som irreducerbara polynomekvationer. Ekvationen $x^3-2=0$ är ett exempel på irreducibel polynomekvation.

Ja! Men avgörande ville Galois fokusera på ekvationer med rationella koefficienter. Eller snarare polynomier med koefficienter som tillhör basfältet. Så vad jag menade var att för $\mathbb Q$ som basfältet är $x^3-2=0$ irreducible.

låt oss överväga $x^2-2x -1=0$ för att ha några ledtrådar. Denna ekvation kan bevisas vara irreducibel. Kommer du ihåg hur man löser det?

Om $b^2-4ac \ geq 0$, ja.

exakt! Så den irreducibla polynomekvationen $x^2 + 2x -1=0$ har två lösningar: $1 + \sqrt{2}$ och $1-\sqrt{2}$… någon kommentar?

Bingo! Det är den viktigaste upptäckten av Galois. Mer allmänt kallas Galois konjugerar alla lösningar till en irreducibel polynomekvation. Och som du kan föreställa dig är dessa viktiga för att ta bort radikaler från nämnare!

det första att märka är att om $x_1$, $x_2$, …, $x_n$ är alla lösningar av en polynom irreducibel ekvation $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ med rationella koefficienter, kan denna polynom irreducibel ekvation faktiskt skrivas om $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Identifiera de konstanta termerna ger sedan $x_1 x_2 … x_n $ = $ (-1)^n a_0/a_n$. Så avgörande är produkten av konjugerade tal det rationella talet $(-1)^n a_0/a_n$, vilket är icke-noll (bevisa det!).

Här är ett litet skämt för att komma ihåg den starka kopplingen mellan konjugat:

Tänk på en bråkdel $1 / x_1$, där $x_1$ är ett komplicerat uttryck med radikaler. Multiplicera upp och ner med konjugaten $x_2$,…, $x_n$ av $x_1$ ger sedan $1/x_1 $=$ (-1)^n a_n x_2…x_n / a_0$, som inte har någon radikal i nämnaren eftersom vi har etablerat $a_0$ för att vara ett icke-nollnummer i basfältet!

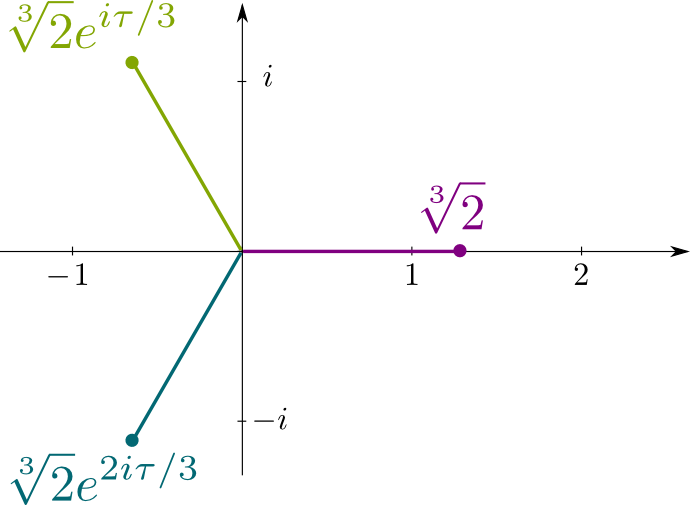
minns att $x^3-2=0$ är den oreducerbara polynomekvationen $\sqrt{2}$ är lösningen av. Så dess konjugat är de andra lösningarna på den ekvationen, som är de komplexa siffrorna $\sqrt{2}j$ och $\sqrt{2}j^2$, där $j= e^{i\tau/3}$ med $\tau = 2\pi$ är förhållandet mellan omkretsen av en cirkel med dess radie. Följande figur visar platserna för konjugatlösningarna i detta komplexa plan:

Galois tvetydighet

slutligen kommer vi till Galois nyckelinsikt!

konjugat är perfekt permutable. Det betyder att om du systematiskt ändrar $ \ sqrt{2}$ Med dess konjugat $-\sqrt{2}$, håller likheterna fortfarande. Till exempel, eftersom vi hade $1/(\sqrt{2}-1) = \sqrt{2}+1$, Kan jag enkelt säga att $1/(-\sqrt{2}-1)=-\sqrt{2}+1$! På samma sätt har vi följande fantastiska implikation:

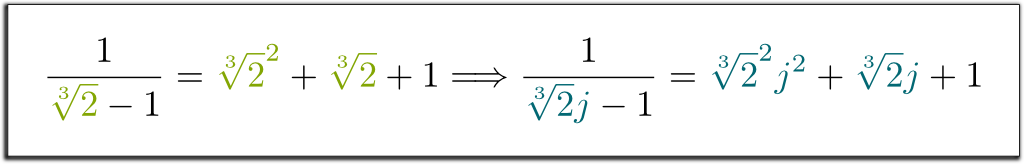
Hehe… Låt mig först komma ihåg att ändliga fält spänns av ett enda element. Så, om basfältet är $\mathbb Q$, Kan något ändligt fält skrivas $\mathbb Q$ för vissa rätt $x_1$. Tänk nu på $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ den irreducibla polynomekvationen $x_1$ är lösningen av. Vad som definierar $\mathbb Q$ är $\mathbb Q$-vektorutrymmet spänt av $x_1$, $x_1^2$, …, $x_1^{n-1}$, med förenkling av större krafter på $x_1$ i enlighet med den algebraiska regeln $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

exakt! Avgörande är att dessa algebraiska regler för $ \ mathbb Q$ inte beror på karaktären av $x_1$; de beror bara på det irreducibla polynomet $x_1$ är lösningen av! Därför är reglerna för $ \ mathbb Q$ identiska med dessa för $ \ mathbb Q$,…, $\mathbb Q$, där $x_1$ ersätts av ett av dess konjugat $x_2$, …, $x_n$. I synnerhet fungerar fälten $\mathbb Q{2}]$ och $\mathbb Q{2} j]$ enligt exakt samma regler. Det är därför konjugat är perfekt permutable! Vi säger att fälten $ \ mathbb Q{2}]$ och $\mathbb Q{2} j]$ är isomorfa, och att ersätta $\sqrt{2}$ med $\sqrt{2}j$ är en isomorfism $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

på ett mycket liknande (men starkare) sätt att två vektorrum med dimension 2 är mer eller mindre desamma! Detta har en fruktansvärd konsekvens. Det betyder att det ur ett algebraiskt perspektiv är meningslöst att göra skillnad mellan ett tal och något av dess konjugat (så länge du systematiskt ersätter numret med dess konjugat)! Så, till exempel, $\sqrt{2}$ och $-\sqrt{2}$ är algebraiskt oskiljbara! För att komma ihåg detta, här är ett annat skämt jag har kommit med:

inte alls! Varje åtskillnad mellan dessa två siffror måste innebära någon annan matematik än algebra, som ordningsrelationer eller topologi. Vad jag menar är att till exempel förhållandet $\sqrt{2} > 0$ gör skillnad mellan $\sqrt{2}$ med $-\sqrt{2}$, men det beror på att det innebär en orderrelation. Men om vi begränsar oss till polynom lika, så är det absolut ingen skillnad mellan $\sqrt{2}$ och $-\sqrt{2}$. På samma sätt är $i$ och $-i$, lösningarna för den irreducibla polynomekvationen $x^2+1=0$, också algebraiskt oskiljbara. Ändå kallar vi godtyckligt $i$ en av dem. Därför kallade Galois sin teori teorin om tvetydighet. Idag kallas tvetydigheten i valet av den konventionella kvadratroten på $-1$ bland $i$ och $-i$ snarare symmetrin mellan $i$ och $-i$.

Galois-grupper

Galois fokuserade särskilt på fältförlängningar som är stabila genom konjugering. Sådana stabila fältförlängningar är nu kända som Galois-förlängningar. Så, om $x_1$ tillhör en Galois-förlängning, innehåller denna Galois-förlängning alla dess konjugat $x_2$,…, $x_n$.

ett enkelt sätt att konstruera Galois-förlängningar består i att ta fältet spänt av lösningar av en irreducibel polynomekvation. Till exempel, om $x_1$,…, $x_n$ är konjugat för basfältet $\mathbb Q$, är $\mathbb Q / \mathbb Q$ En Galois-förlängning. Fält som konstruerats på detta sätt kallas delningsfält.

till exempel är delningsfältet för ekvation $x^3-2=0$ Galois-förlängningen $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ spänner över sina lösningar.

om $x_1 $ spänner över en Galois-förlängning, gör det också dess konjugat. Således $ \ mathbb Q = \mathbb Q = $ … $ = \mathbb Q$ = $\mathbb Q$. Således är isomorfismen mellan $ \ mathbb Q$ och $\mathbb Q$ som består i att alltid ersätta $x_1$ med $x_2$ faktiskt en isomorfism mellan $\mathbb Q$ och sig själv! Vi kallar det en automorfism. Automorfismer av en Galois-förlängning $ \ mathbb Q / \mathbb Q$ bildar Galois-gruppen $ Gal (\mathbb Q/\mathbb Q)$.

nu, avgörande, om $ \ mathbb Q = \mathbb Q$, då alla automorfismer av en Galois förlängning $ \ mathbb Q / \mathbb Q$ är permutationer av $x_1$ med en av dess konjugat! I synnerhet ser vi här att kardinaliteten hos en Galois-grupp är lika med graden av Galois-förlängningen.

visst! Du kan märka att $ \ mathbb Q = \mathbb Q$ och $\mathbb Q = \mathbb Q$, vilket innebär att $i$ och $\sqrt{2}$ vardera spänner över delningsfälten i den irreducibla polynomekvationen de är lösning på. Således är $ \ mathbb Q / \mathbb Q$ och $\mathbb Q/\mathbb Q$ båda Galois-tillägg. Därför består deras automorfismer i att ersätta $i$ med ett av dess konjugat, $i$ eller $- i$ och ersätta $\sqrt{2}$ med $\sqrt{2}$ eller $ – \sqrt{2}$. I de första fallen ändrar vi ingenting till siffror, vilket motsvarar nollsymmetri. De andra fallen kan visualiseras som axiella symmetrier, som visas i figuren nedan:

är det inte fantastiskt?

visst! Låt oss komma till delningsfältet $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2]$ av $x^3-2=0$. Men innan vi går vidare, Låt oss märka att $ \ mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.

allt vi behöver bevisa är att alla generatorer i ett fält tillhör det andra. Låt oss börja med att bevisa att generatorerna för den senare, $\sqrt{2}$ och $j$, tillhör den förra. Det är uppenbart för $ \ sqrt{2}$. Nu $j = (\sqrt{2} j) / \sqrt{2}$, alltså $j$ tillhör det tidigare fältet också. Detta bevisar att alla element i $ \ mathbb Q{2},j]$ tillhör $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Ömsesidigt är det enkelt att alla generatorer i det tidigare fältet, $ \ sqrt{2}$, $\sqrt{2}j$ och $\sqrt{2}j^2$, är produkter från generatorerna för den senare. Således är båda fälten lika. Och i synnerhet $ \ mathbb Q{2}, j]/\mathbb Q$ är en Galois-förlängning.

Hehe … för att förstå symmetrierna för $ \ mathbb Q{2}]$ måste vi gå vidare i Galois studie av Galois-grupper …

Galois-korrespondens

problemet med Galois-grupper är att de kan bli extremt stora och komplicerade. Detta är särskilt fallet med den oändliga gruppen $Gal (\bar {\mathbb Q}/ \ mathbb Q)$. För att gripa så stora och komplexa grupper hade Galois den lysande tanken att bryta dessa i mindre bitar.

förvånansvärt upptäckte Galois att Galois-grupper kunde delas in i undergrupper av symmetrier genom att bara titta på de som lämnar något underfält oförändrat. Till exempel $\mathbb Q$ är ett underfält av $\mathbb Q{2},j]$, eftersom något nummer av det förra tillhör det senare. Således bildar symmetrier av $ \ mathbb Q{2},j]$ som inte ändrar något till $\mathbb Q$ en undergrupp av Galois-gruppen av $\mathbb Q{2},j]/\mathbb Q$. Dessa symmetrier bildar Galois-gruppen $ Gal (\mathbb Q{2},j]/\mathbb Q)$.

Jag vet! Jag gillar att visualisera dessa symmetrier som sätt att ansluta $\mathbb Q{2},j]$ till $\mathbb Q$. Här är en avbildad bild av ”plugging on”:

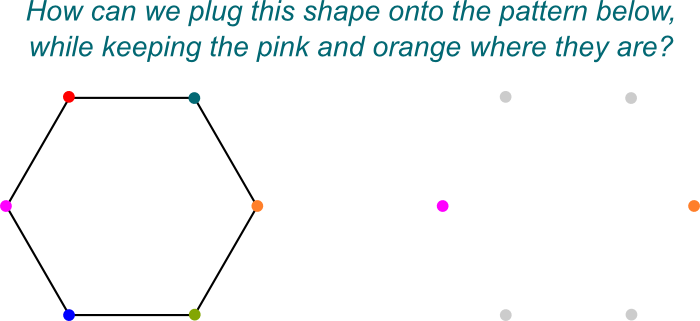
exakt! Och det är helt enkelt för att $ \ mathbb Q{2},j]$ är en Galois-förlängning av $\mathbb Q$ som i sig är en fältförlängning av $\mathbb Q$.

och det finns mer! Galois visade att alla undergrupper av en Galois förlängningar erhålls på detta sätt! Mer exakt är kartläggningen av något fält $K$ mellan Galois-förlängningen $ \ mathbb Q{2},j]$ och basfältet $\mathbb Q$ till Galois-gruppen $Gal(\mathbb Q{2},j] / K)$ bijektivt. Detta faktum kallas Galois-korrespondensen! Denna korrespondens visas schematiskt nedan för en Galois-förlängning $ \ mathbb Q / \mathbb Q$.

istället för att försöka beskriva denna grupp direkt, låt oss fokusera på dess undergrupp $Gal(\mathbb Q{2}, j]/\mathbb Q)$. Det är enkelt att $ \ sqrt{2}$ spänner $\mathbb Q{2},j]$ när den läggs till $\mathbb Q$. Således är $\mathbb Q{2},j]/\mathbb Q$ En Galois-förlängning som spänner över $ \ sqrt{2}$. Därför, med hjälp av en sats som vi har sett tidigare, vet vi att alla automorfismer i denna Galois-förlängning består i att ersätta $\sqrt{2}$ med en av dess 3 konjugat (själv, $\sqrt{2} j$ och $\sqrt{2} j^2$)!

nu kunde jag fortsätta studera andra bitar av $Gal (\mathbb Q{2}, j]/\mathbb Q)$, som Galois-undergruppen $Gal (\mathbb Q{2},j]/\mathbb Q{2}])$. Men jag använder hellre en annan av Galois kraftfulla satser. Han bevisade nämligen att om $\mathbb Q/\mathbb Q$ dessutom var en Galois-förlängning, så är undergruppen $Gal(\mathbb Q{2}, j]/\mathbb Q)$ normalt.

Således kan Galois-gruppen av $ \ mathbb Q{2},j]/\mathbb Q$ kvoteras av denna undergrupp, och kvotientgruppen är då lika med $Gal(\mathbb Q/\mathbb Q)$. Ändå är $ \ mathbb Q / \mathbb Q$ verkligen en Galois-förlängning som spänner över $j$, vars konjugat är $j^2$. Således består$ Gal (\mathbb Q/\mathbb Q)$ i att antingen lämna $j$ som $j$ eller ersätta den med $j^2$.

Vi kan nu härleda alla symmetrier av $Gal (\mathbb Q{2},j]/\mathbb Q)$ genom att kombinera dessa av $Gal(\mathbb Q{2},j] / \mathbb Q)$ och $Gal(\mathbb Q/\mathbb Q)$. Vi kan visa dessa symmetrier genom att rita hur de påverkar våra tre spännviddskonjugat $\sqrt{2}$, $\sqrt{2}j$ och $\sqrt{2}j^2$:

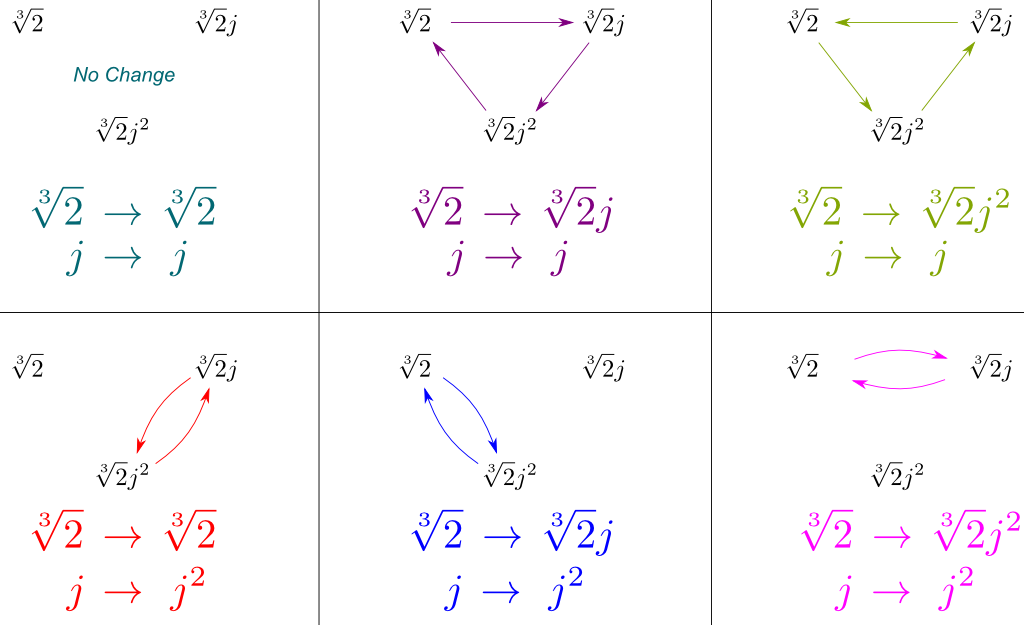
avgörande, figuren ovan innehåller alla symmetrier av $Gal (\mathbb Q{2},j]/\mathbb Q)$. Och förvånansvärt motsvarar dessa symmetrier den välkända gruppen av symmetri.

Jag låter Marcus du Sautoy presentera det för dig:

så, är symmetrier här som en sjöstjärna eller som en triangel?

Ja, verkligen! Denna grupp av symmetrier i triangeln kallas $D_3$, och den är densamma som gruppen $S_3$ av permutationer av 3 element. Detta leder oss till följande formel, som jag tyckte var så vacker, att jag har bestämt mig för att rama in den!

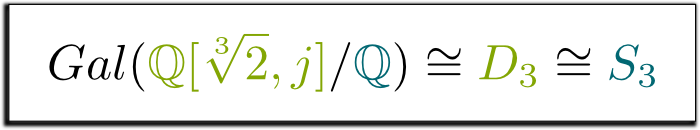
Låt oss avsluta

på många sätt ska Galois betraktas som fadern till modern algebra. Hans viktigaste insikt var att titta på matematik genom vinkeln på reglerna för verksamheten, och detta ledde honom att avslöja överraskande och insiktsfulla oklarheter, eller symmetrier, mellan siffror. Ur ett algebraiskt perspektiv är siffror som $ \ sqrt{2}$, $\sqrt{2}j$ och $\sqrt{2}j^2$ verkligen perfekt symmetriska och helt utbytbara.

förståelsen av dessa symmetrier har haft häpnadsväckande tillämpningar inom algebraisk geometri och algebraisk topologi bland andra. I synnerhet tidiga framgångar med teorin inkluderar en klassificering av konstruerbara regelbundna polygoner och en sats som hävdar att hög grad polynomekvationer inte kunde lösas av radikaler.

de senaste framgångarna förekommer i kryptografi och Andrew Wiles bevis på Fermats sista sats. Detta bevis innebär att studera Galois-gruppen $Gal (\bar {\mathbb Q} / \ mathbb Q)$ med grupprepresentation. Men jag skulle säga att teorin på något sätt fortfarande är ung, och mycket finns kvar att upptäcka. Det är trots allt ett av de mest aktiva forskningsområdena i dagens rena matematikforskning.

detta borde leda oss att betala många fler hyllningar till Galois otroliga geni … Låt mig inkludera en av SocraticaStudios.