där PA och pB är frekvenserna för alleler A och B vid två separata loci (X, Y) mätt för N-individer är pab frekvensen för haplotypen med alleler a och B i den studerade populationen, X och Y är de genomsnittliga genotypfrekvenserna för den första respektive andra platsen, XI är genotypen för individ i vid den första platsen och Yi är genotypen för individ i vid den andra platsen. Ekvation (2) korrelerar de genotypiska allelräkningarna istället för haplotypfrekvenserna och påverkas inte av dubbla heterozygoter (detta tillvägagångssätt resulterar i samma uppskattningar som –r2-alternativet i PLINK).SNeP uppskattar den historiska effektiva befolkningsstorleken baserat på förhållandet mellan r2, Ne och c (rekombinationshastighet), (ekvation 3-Sved, 1971) och gör det möjligt för användare att inkludera korrigeringar för provstorlek och osäkerhet i gametisk fas (ekvation 4—Weir och Hill, 1980):

där n är antalet enskilda provtagningar, är det 2 när den gametiska fasen är känd och är 1 om istället fasen inte är känd.

flera approximationer används för att dra slutsatsen om rekombinationshastigheten med hjälp av det fysiska avståndet (XHamster) mellan två loci som referens och översätta det till länkavstånd (d), som vanligtvis beskrivs som Mb(msk), cm(d). För små värden på d är den senare approximationen giltig, men för större värden på d ökar sannolikheten för flera rekombinationshändelser och störningar, dessutom är förhållandet mellan kartavstånd och rekombinationshastighet inte linjärt, eftersom den maximala rekombinationshastigheten är 0,5. Således, om man inte använder mycket kort gastronomi, är approximationen D. C. inte idealisk (Corbin et al., 2012). Vi implementerade därför kartläggningsfunktioner för att översätta den beräknade d till c, efter Haldane (1919), Kosambi (1943), Sved (1971) och Sved och Feldman (1973). Ursprungligen härleder SNeP d för varje par SNP: er som direkt proportionell mot exporten enligt D = K, där k är ett användardefinierat rekombinationshastighetsvärde (Standardvärdet är 10-8 som i Mb = cM). Det härledda värdet av Macau kan sedan utsättas för en av de tillgängliga kartläggningsfunktionerna om det krävs av användaren.

lösa ekvation (3) för Ne och inklusive alla korrigeringar som beskrivs, tillåter förutsägelse av Ne från LD-data med hjälp av (Corbin et al., 2012):

där Nt är den effektiva populationsstorleken t generationer sedan beräknad som t = (2F(ct)) -1 (Hayes et al., 2003), ct är rekombinationshastigheten definierad för ett specifikt fysiskt avstånd mellan markörer och eventuellt justerat med de kartläggningsfunktioner som nämns ovan, r2adj är LD-värdet justerat för provstorlek och XHamster:= {1, 2, 2.2} är en korrigering för förekomsten av mutationer (Ohta och Kimura, 1971). Därför, LD över större rekombinanta avstånd är informativ på senaste Ne medan kortare avstånd ger information om mer avlägsna tider tidigare. Ett binningssystem implementeras för att erhålla genomsnittliga r2-värden som återspeglar LD för specifika inter-locus-avstånd. Det implementerade binningssystemet använder följande formel för att definiera minimi-och maximivärdena för varje bin:

där bi (Aug 1) är ith-facket för det totala antalet fack (totBins), minD och maxD är respektive minsta och maximala avståndet mellan SNP: er och X är ett positivt reellt tal (20) när X är lika med 1, fördelningen av avstånd mellan facken är linjär och varje fack har samma avståndsområde. För större värden på x ändras fördelningen av avstånd vilket möjliggör ett större intervall på de sista facken och ett mindre intervall på de första facken. Genom att variera denna parameter kan användaren ha ett tillräckligt antal parvisa jämförelser för att bidra till den slutliga ne-uppskattningen för varje bin.

Exempelapplikation

Vi testade SNeP med två publicerade dataset som tidigare använts för att beskriva trender i Ne över tid med LD, Bos indicus och Ovis aries . R2-uppskattningarna för nötkreatursdatauppsättningarna erhölls av författarna som använde GenABLE (Aulchenko et al., 2007) med en minsta allelfrekvens (MAF) < 0.01 och justering av rekombinationshastigheten med hjälp av Haldanes kartläggningsfunktion (Haldane, 1919). R2-uppskattningarna av fårdata beräknades av författarna med PLINK-1.07 (Purcell et al., 2007), med en MAF < 0.05 och inga ytterligare korrigeringar. För båda autosomala datamängder R2 uppskattningar där korrigerade för provstorlek med hjälp av ekvation (4) med GHz = 2. För dessa jämförande analyser inkluderade kommandoraden SNeP samma parametrar som användes för de publicerade uppgifterna bortsett från R2-uppskattningarna, beräknade genom genotypantal och användningen av Sneps nya binningstrategi.

resultat

SNeP är en flertrådad applikation utvecklad i C++ och binärer för de vanligaste operativsystemen (Windows, OSX och Linux) kan laddas ner frånhttps://sourceforge.net/projects/snepnetrends/. Binärfilerna åtföljs av en manual som beskriver steg-för-steg-användningen av SNeP för att härleda trender i Ne som beskrivs här. SNeP producerar en utdatafil med tabbavgränsade kolumner som visar följande för varje bin som användes för att uppskatta Ne: antalet generationer i det förflutna som bin motsvarar (t. ex., 50 generationer sedan), motsvarande ne-uppskattning, det genomsnittliga avståndet mellan varje par SNP i facket, den genomsnittliga r2 och standardavvikelsen för r2 i facket och antalet SNP som används för att beräkna r2 i facket. Den här filen kan enkelt importeras i Microsoft Excel, R eller annan programvara för att plotta resultaten. Tomterna som visas här (figurerna 1, 3) motsvarar kolumnerna för generationer sedan och Ne från utdatafilen. Kolumnen med R2-standardavvikelsen tillhandahålls för användare att inspektera variansen i ne-uppskattningen i varje fack, särskilt för de fack som återspeglar äldre tidsberäkningar och som är mindre tillförlitliga eftersom antalet SNP som används för att uppskatta r2 blir mindre.

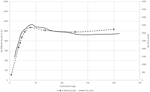
Figur 1. Jämförelse av Ne-trender för sex Schweiziska fårraser enligt Burren et al. (2014) (streckade linjer) och detta arbete (heldragna linjer).

det format som krävs för indatafilerna är standard PLINK-formatet (ped-och kartfiler) (Purcell et al., 2007). SNeP tillåter användarna att antingen beräkna LD på data som beskrivits ovan, eller använda en anpassad förkalkylerad ld-matris för att uppskatta Ne med ekvation (5).

programvarugränssnittet tillåter användaren att styra alla parametrar i analysen, t.ex. avståndsområdet mellan SNP i bp och uppsättningen kromosomer som används i analysen (t. ex. 20-23). Dessutom inkluderar SNeP möjligheten att välja en MAF-tröskel (standard 0.05), eftersom det har visats att redovisning av MAF resulterar i objektiva R2-uppskattningar oavsett provstorlek (Sved et al., 2008). Sneps multithreaded arkitektur möjliggör snabb beräkning av stora dataset (vi testade upp till ~100k SNP för en enda kromosom), till exempel analyserades BOS-data som beskrivs här med en processor i 2’43”, användningen av två processorer minskade tiden till 1’43”, fyra processorer minskade analystiden till 1’05”.

Zebu exempel

för zebu-analysen visade formerna av Ne-kurvorna erhållna med SNeP och deras publicerade datatrender samma bana med en jämn nedgång fram till omkring 150 generationer sedan, följt av en expansion med en topp runt 40 generationer sedan och slutade i en brant nedgång på de senaste generationerna (Figur 1). Men medan trenderna i båda kurvorna var desamma resulterade de två tillvägagångssätten i olika ne-uppskattningar, med Sneps värden ungefär tre gånger större än de i originalpapperet. Medan vi försökte använda författarnas parametrar i våra analyser var vissa skillnader oundvikliga, det vill säga den ursprungliga publiceringen av nötkreatursdata uppskattade r2 med en annan inställning till den som implementerades i SNeP. Analyser med SNeP baserades på genotyper, medan den ursprungliga analysen baserades på härledda två locus haplotyper, vilket resulterar i publicerade data som visar en förväntad r2 på 0,32 vid minsta avstånd, medan våra uppskattningar var 0,23. Liknande, Mbole-Kariuki et al. (2014) erhöll en bakgrundsnivå r2 = 0.013 runt 2 Mb, medan vår uppskattning på samma avstånd var 0.0035 (data visas inte). Följaktligen, eftersom våra uppskattningar av LD var konsekvent mindre än Mbole-Kariuki et al. (2014) Det förväntas att våra ne-uppskattningar borde vara större. Även om denna observation belyser vikten av ett noggrant val av parametrarna och deras tröskelvärden, är det viktigt att lyfta fram att även om den absoluta storleken på Ne-värdena är annorlunda, är trenderna nästan identiska.

Schweiziskt Fårexempel

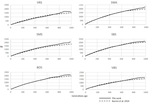
de sex Schweiziska fårraserna som analyserades med SNeP gav jämförbara resultat med de från originalpapperet (Figur 2), med mestadels överlappande ne-trendkurvor (Figur 3). Den allmänna trenden i Ne visade dock en nedgång mot nutiden. SNeP producerade något större värden av Ne för det mer avlägsna förflutna (700-800 generationer). Detta beror på det olika binning-systemet som används i SNeP, vilket gör det möjligt för användaren att få en jämnare fördelning av parvisa jämförelser inom varje fack (dvs., antalet SNP parvisa jämförelser inom varje fack är jämförbart). För den tidsperiod som sträcker sig längre än 400 generationer sedan, Burren et al. (2014) använde endast tre fack i sin analys (centrerad vid 400, 667 och 2000 generationer sedan) medan SNeP för samma tidsperiod använde 5 fack med ett antal parvisa jämförelser beroende på intervallet definierat med formler 6a, b. följaktligen slutar Burren och kollegors tillvägagångssätt med en högre densitet av data som beskriver de senaste generationerna än att beskriva de äldsta generationerna. Därför tenderar användningen av färre fack att öka närvaron av mindre värden på Ne i varje fack, vilket sänker det genomsnittliga ne-värdet för varje fack. Ne-värdena för det senaste förflutna, jämfört vid den 29: e generationen tidigare, gav mycket liknande resultat. Den största skillnaden (50) erhölls för SBS-rasen.

Figur 2. Jämförelse mellan de senaste ne-värdena beräknade vid 29: e generationen i detta arbete och Burren et al. (2014) för sex Schweiziska fårraser.

Figur 3. Jämförelse av Ne-trender för de senaste 250 generationerna i SHZ-data som erhållits av Mbole-Kariuki et al. (2014) (streckad linje) och använda SNeP (heldragen linje).

diskussion

analys av Ne med LD-data demonstrerades först för 40 år sedan och har tillämpats, utvecklats och förbättrats sedan (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Det traditionellt lilla antalet SNP-analyserade är inte längre en begränsning, eftersom SNP-Chips består av ett extremt stort antal SNP, tillgängliga på kort tid och till ett rimligt pris. Detta har ökat användningen av metoden, som har tillämpats på människor (Tenesa et al., 2007; McEvoy et al., 2011) samt till flera domesticerade arter (England et al., 2006; Uimari och Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Tillsammans med dessa förbättringar har metodologiska begränsningar blivit uppenbara och har tagits upp här, med majoriteten av ansträngningarna som pekar på den korrekta uppskattningen av den senaste Ne. Ändå är det kvantitativa värdet av uppskattningen mycket beroende av provstorlek, typen av LD-uppskattning och binningsprocessen (Waples and Do, 2008; Corbin et al., 2012), medan dess kvalitativa mönster beror mer på den genetiska informationen än på datamanipulation.

hittills har denna metod tillämpats med hjälp av en mängd olika programvaror, det finns ingen standardiserad metod för att bin resultaten och varje studie har tillämpat ett mer eller mindre godtyckligt tillvägagångssätt, t.ex. binning för generationsklasser tidigare (Corbin et al., 2012), binning för avståndsklasser med ett konstant intervall för varje fack (Kijas et al., 2012) eller binning per distansklasser på linjärt sätt men med större fack för de senaste tidpunkterna (Burren et al., 2014). Så vitt vi vet är den enda tillgängliga programvaran som uppskattar Ne genom LD NeEstimator (Do et al., 2014), en uppgraderad version av den tidigare LDNE (Waples och Do, 2008) som möjliggör analys av stora dataset (som 50k SNPChip). Viktigt, medan SNeP fokuserar på att uppskatta historiska ne-trender, neestimators mål är att producera samtida objektiva ne-uppskattningar, bör den senare därför betraktas som ett kompletterande verktyg när man undersöker demografi genom LD.

Vi använde SNeP för att analysera två datamängder där metoden tidigare tillämpades. Resultaten vi fick för fårdata var både kvantitativt och kvalitativt jämförbara med de som erhållits av Burren et al. (2014), medan vi för Zebu-uppgifterna fick en ne-trendberäkning som nära matchade Mbole-Kariuki et al. (2014) även om våra punktuppskattningar av Ne var större än de som beskrivs för data (Mbole-Kariuki et al., 2014). Skillnaden mellan dessa två resultat återspeglar att Burren och kollegor producerade sina R2-uppskattningar med PLINK (standardprogramvaran för storskalig SNP-datamanipulation) som använder samma tillvägagångssätt som används för att uppskatta r2 av SNeP, medan Mbole-Kariuki et al. följt Hao et al. (2007) för R2 uppskattning. Användningen av olika uppskattningar för LD är avgörande för den kvantitativa aspekten av Ne-kurvan, där på grund av den hyperboliska korrelationen mellan Ne och r2 kan en minskning av r2 på dess intervall närmare 0 leda till en mycket stor förändring av Ne-uppskattningar, medan skillnader i uppskattningar är mindre signifikanta när r2-värdet är högt, dvs närmare 1. Därför, även om Ne-värdena i en av datamängderna var väsentligt olika, överlappade ne-kurvorna i båda fallen med de som ursprungligen publicerades.

som redan föreslagits av andra författare måste tillförlitligheten hos de kvantitativa uppskattningarna som erhållits med denna metod tas med försiktighet, särskilt för ne-värden relaterade till de senaste och äldsta generationerna (Corbin et al., 2012) för de senaste generationerna är stora värden på c involverade, inte passande de teoretiska implikationerna som Hayes föreslog att uppskatta en variabel Ne över tiden (Hayes et al., 2003). Uppskattningar för de äldsta generationerna kan också vara opålitliga eftersom koalescerande teori visar att ingen SNP kan samplas pålitligt efter 4Ne generationer tidigare (Corbin et al., 2012). Vidare påverkas ne-uppskattningar, och särskilt de som är relaterade till generationer längre tidigare, starkt av datamanipulationsfaktorer, såsom valet av MAF-och alfavärden. Dessutom kan den tillämpade binningsstrategin störa metodens allmänna precision, till exempel där ett otillräckligt antal parvisa jämförelser används för att fylla varje bin.

en av tillämpningarna av metoden är att jämföra rasdemografier. I detta fall skulle formen på NE-kurvorna vara det optimala verktyget för att differentiera olika demografiska historier, mer än deras numeriska värden, genom att använda dem som ett potentiellt demografiskt fingeravtryck för den rasen eller arten, men med hänsyn till att mutation, migration och urval kan påverka ne-uppskattningen genom LD (Waples and Do, 2010). Dessutom är noggrann övervägande av de data som analyseras med SNeP (och annan programvara för att uppskatta Ne) mycket viktigt, eftersom förekomsten av förvirrande faktorer som blandning kan leda till fördjupade uppskattningar av Ne (Orozco-terWengel och Bruford, 2014).syftet med SNeP är därför att tillhandahålla ett snabbt och pålitligt verktyg för att tillämpa LD-metoder för att uppskatta ne med hjälp av genotypiska data med hög genomströmning på ett mer konsekvent sätt. Det tillåter två olika R2-uppskattningsmetoder plus möjligheten att använda r2-uppskattningar från extern programvara. Användningen av SNeP övervinner inte gränserna för metoden och teorin bakom den, men det gör det möjligt för användaren att tillämpa teorin med alla korrigeringar som hittills föreslagits.

Författarbidrag

MB utformade och skrev programvaran och manuskriptet. MB, MT och POtW testade programvaran och utförde analyserna. MT, POtW och MWB reviderade manuskriptet. Alla författare godkände det slutliga manuskriptet.

intressekonflikt uttalande

författarna förklarar att forskningen genomfördes i avsaknad av kommersiella eller finansiella relationer som kan tolkas som en potentiell intressekonflikt.

bekräftelser

Vi tackar Christine Flury för att tillhandahålla fårdata och för användbar diskussion. Vi tackar också de två granskarna för användbara förslag för att förbättra detta dokument. MB stöddes av programmet Master och Back (Regione Sardegna).