Prealgebra
lärandemål
- hitta området, basen och höjden på en triangel
- hitta längden på ena sidan av en triangel med omkretsen och två andra längder
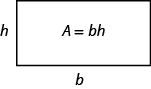
Vi vet nu hur vi hittar området för en rektangel. Vi kan använda detta faktum för att hjälpa oss att visualisera formeln för området för en triangel. I rektangeln nedan har vi märkt längden b och bredden h, så det är området är bh.
området för en rektangel är basen, b, gånger höjden, h.
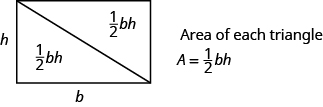
vi kan dela denna rektangel i två kongruenta trianglar (se bilden nedan). Trianglar som är kongruenta har identiska sidolängder och vinklar, och så är deras områden lika. Området för varje triangel är hälften av rektangelns yta, eller \ frac{1}{2}bh. Detta exempel hjälper oss att se varför formeln för området för en triangel är A=\frac{1}{2}bh.
en rektangel kan delas in i två trianglar med samma yta. Området för varje triangel är hälften av rektangelns yta.
formeln för området för en triangel är A=\frac{1}{2}bh, där b är basen och h är höjden.
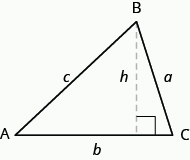
för att hitta området i triangeln måste du veta dess bas och höjd. Basen är längden på ena sidan av triangeln, vanligtvis sidan längst ner. Höjden är längden på linjen som förbinder basen till motsatt toppunkt och gör en \text{90}^ \circ vinkel med basen. Bilden nedan visar tre trianglar med basen och höjden på varje markerad.
höjden h i en triangel är längden på ett linjesegment som förbinder basen till motsatt toppunkt och gör en \text{90}^ \circ vinkel med basen.

Triangelegenskaper
för varje triangel \ Delta ABC är summan av måtten på vinklarna \text{180}^ \circ.
m\vinkel{a}+m\vinkel{B}+m\vinkel{C}=180^ \ circ
omkretsen av en triangel är summan av sidornas längder.
P = a + b + c
området för en triangel är hälften av basen, b, gånger höjden, h.
A= \ frac{1}{2}bh
exempel
hitta området för en triangel vars bas är 11 tum och vars höjd är 8 tum.
lösning
| Steg 1. Läs problemet. Rita figuren och märk den med den angivna informationen. | 
|
| steg 2. Identifiera vad du letar efter. | området för triangeln |
| steg 3. Namn. Välj en variabel för att representera den. | låt A = område av triangeln |
| steg 4.Översätta.
skriv rätt formel. ersättare. |
 |
| Steg 5. Lös ekvationen. | A=44 kvadrattum. |
| steg 6. Kontrollera:
A= \ frac{1}{2}bh 44\stackrel{?} { = } \frac{1}{2}(11)8 44=44 \ bock |
|
| Steg 7. Svara på frågan. | området är 44 kvadrattum. |
prova det
exempel
omkretsen av en triangulär trädgård är 24 fot. Längderna på två sidor är 4 fot och 9 fot. Hur lång är den tredje sidan?
prova det
exempel
området för ett triangulärt kyrkfönster är 90 kvadratmeter. Fönstrets botten är 15 meter. Vad är fönstrets höjd?
prova det
Isosceles och liksidiga trianglar
förutom den högra triangeln har vissa andra trianglar speciella namn. En triangel med två sidor av samma längd kallas en likriktad triangel. En triangel som har tre sidor av samma längd kallas en liksidig triangel. Bilden nedan visar båda typerna av trianglar.
i en likriktad triangel har två sidor samma längd och den tredje sidan är basen. I en liksidig triangel har alla tre sidor samma längd.
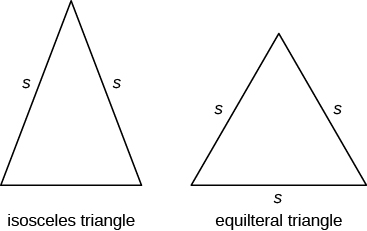
Isosceles och liksidiga trianglar
en isosceles triangel har två sidor samma längd.
en liksidig triangel har tre sidor av samma längd.
exempel
omkretsen av en liksidig triangel är 93 tum. Hitta längden på varje sida.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. Scarf kommer att vara en likriktad triangel med en bas på
60 tum. Hur länge kan hon göra de två lika sidorna?








