sensorfusion
Kalman-filter
algoritmen som används för att sammanfoga data kallas ett Kalman-filter.
Kalman-filtret är en av de mest populära algoritmerna i datafusion. Uppfanns 1960 av Rudolph Kalman, det används nu i våra telefoner eller satelliter för navigering och spårning. Den mest kända användningen av filtret var under Apollo 11-uppdraget att skicka och föra besättningen tillbaka till månen.
När ska man använda ett Kalman-Filter ?
ett Kalman-filter kan användas för datafusion för att uppskatta tillståndet för ett dynamiskt system (utvecklas med tiden) i nuet (filtrering), det förflutna (utjämning) eller framtiden (förutsägelse). Sensorer inbäddade i autonoma fordon avger åtgärder som ibland är ofullständiga och bullriga. Sensorns felaktighet (brus) är ett mycket viktigt problem och kan hanteras av Kalman-filtren.
ett Kalman-filter används för att uppskatta tillståndet för ett system, betecknat x. denna vektor består av en position p och en hastighet v.

vid varje uppskattning associerar vi ett mått på osäkerhet P.
genom att utföra en fusion av sensorer tar vi hänsyn till olika data för samma objekt. En radar kan uppskatta att en fotgängare är 10 meter bort medan Lidar uppskattar att den är 12 meter. Användningen av Kalman-filter gör att du kan få en exakt uppfattning om hur många meter som verkligen är fotgängaren genom att eliminera bruset från de två sensorerna.
ett Kalman-filter kan generera uppskattningar av tillståndet för objekt runt det. För att göra en uppskattning behöver den bara de aktuella observationerna och den tidigare förutsägelsen. Mäthistoriken är inte nödvändig. Detta verktyg är därför lätt och förbättras med tiden.
hur det ser ut
tillstånd och osäkerhet representeras av Gaussier.

en Gaussian är en kontinuerlig funktion under vilken området är 1. Detta gör att vi kan representera sannolikheter. Vi är på en sannolikhet för normalfördelning. Kalman-filtrets uni-modalitet innebär att vi har en enda topp varje gång för att uppskatta systemets tillstånd.
. Ju större variansen desto större osäkerhet.
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.
Bayesian Filtering
In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Vi använder observationerna från våra sensorer för att korrigera det förutsagda tillståndet och få en mer exakt uppskattning.
För att göra en uppskattning behöver ett Kalman-filter bara aktuella observationer och föregående förutsägelse. Mäthistoriken är inte nödvändig.
Maths
matematiken bakom Kalman-filtren är gjorda av tillägg och multiplikationer av matriser. Vi har två steg: förutsägelse och uppdatering.
förutsägelse
vår förutsägelse består av att uppskatta ett tillstånd x ’och en osäkerhet P’ vid tiden t från de tidigare tillstånden x och P vid tiden t-1.
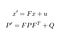
- f: övergångsmatris från T-1 till t
- xhamster: brus tillagt
- Q: Kovariansmatris inklusive brus
Uppdatering
uppdateringsfasen består av att använda en z-mätning från en sensor för att korrigera vår förutsägelse och därmed förutsäga x och P.
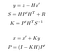
- y: skillnad mellan faktisk mätning och förutsägelse, dvs felet.
- S: uppskattat systemfel
- H: Övergångsmatris mellan sensorns markör och vår.
- R: Kovariansmatris relaterad till sensorbrus (ges av sensortillverkaren).
- K: Kalman vinst. Koefficient mellan 0 och 1 återspeglar behovet av att korrigera vår förutsägelse.
uppdateringsfasen gör det möjligt att uppskatta ett x och ett P närmare verkligheten än vad mätningarna ger.
ett Kalman-filter tillåter förutsägelser i realtid, utan data i förväg. Vi använder en matematisk modell baserad på multiplikation av matriser för varje gång som definierar ett tillstånd x (position, hastighet) och osäkerhet P.
omtryckt tidigare/bakre
detta diagram visar vad som händer i ett Kalman-filter.

- predicted State estimate representerar vår första uppskattning, vår förutsägelsesfas. Vi pratar om prior.
- mätning är mätningen från en av våra sensorer. Vi har bättre osäkerhet men sensorns brus gör det till en mätning som alltid är svår att uppskatta. Vi pratar om Sannolikhet.
- Optimal Tillståndsuppskattning är vår uppdateringsfas. Osäkerheten är den här gången den svagaste, vi samlade information och fick generera ett värde mer säkert än med vår sensor ensam. Detta värde är vår bästa gissning. Vi talar om posterior.
vad ett Kalman-filter implementerar är faktiskt en Bayes-regel.

i ett Kalman-filter slingrar vi förutsägelser från mätningar. Våra förutsägelser är alltid mer exakta eftersom vi håller ett mått på osäkerhet och regelbundet beräknar felet mellan vår förutsägelse och verklighet. Vi kan från matrismultiplikationer och sannolikhetsformler uppskatta hastigheter och positioner för fordon runt omkring oss.
” utökade/oparfymerade ” filter och icke-linjäritet
ett väsentligt problem uppstår. Våra matematiska formler implementeras alla med linjära funktioner av typen y = ax + b.
ett Kalman-filter fungerar alltid med linjära funktioner. Å andra sidan, när vi använder en Radar, är data inte linjära.

radaren ser världen med tre mått:
dessa tre värden gör vår mätning till en olinjär med tanke på inkluderingen av vinkeln Bisexuell.
vårt mål här är att konvertera data till kartesiska data (px, py, vx, vy).
om vi anger icke-linjära data i ett Kalman-filter är vårt resultat inte längre i uni-modal Gaussisk form och vi kan inte längre uppskatta position och hastighet.

Så vi använder approximationer, varför vi arbetar med två metoder:
– utökade Kalman-filter använder Jacobian och Taylor-serien för att linjärera modellen.
– Unscented Kalman filter använder en mer exakt approximation för att linjärisera modellen.
för att hantera införandet av icke-linjäritet av radaren finns tekniker och tillåter våra filter att uppskatta position och hastighet för de objekt som vi vill spåra.