under vissa omständigheter bidrar strömmen i lindningen av en toroidal induktor endast till B-fältet inuti lindningarna och bidrar inte till det magnetiska B-fältet utanför lindningarna. Detta är en följd av symmetri och amp Bisexre s circuital lag.

tillräckliga villkor för total intern inneslutning av B-fältetredigera

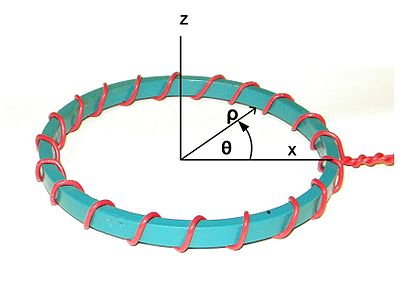Fig. 1. Koordinatsystem. Z-axeln är den nominella symmetriaxeln. X-axeln väljs godtyckligt för att rada upp med startpunkten för lindningen. den kallas den radiella riktningen. det kallas den perifera riktningen.

Fig. 2. En axiellt symmetrisk toroidal induktor utan omkretsström.

frånvaron av omkretsström (banan för omkretsström indikeras med den röda pilen i Figur 3 i detta avsnitt) och den axiellt symmetriska layouten för ledarna och magnetiska material är tillräckliga förutsättningar för total intern inneslutning av B-fältet. (Vissa författare föredrar att använda H-fältet). På grund av symmetrin måste linjerna i b-flödet bilda cirklar med konstant intensitet centrerad på symmetriaxeln. De enda linjerna av B-flöde som omger någon ström är de som ligger inuti den toroidala lindningen. Därför, från Ampere circuital lag, måste intensiteten hos B-fältet vara noll utanför lindningarna.

Fig. 3. Toroidal induktor med omkretsström

Figur 3 i detta avsnitt visar den vanligaste toroidala lindningen. Det misslyckas båda kraven för total B fält inneslutning. Ser ut från axeln, ibland är lindningen på insidan av kärnan och ibland är den på utsidan av kärnan. Det är inte axiellt symmetriskt i närområdet. Men vid punkter ett avstånd av flera gånger lindningsavståndet ser toroiden symmetrisk ut. Det finns fortfarande problemet med omkretsströmmen. Oavsett hur många gånger lindningen omger kärnan och oavsett hur tunn tråden är, kommer denna toroidala induktor fortfarande att innehålla en spolslinga i toroidplanet. Denna lindning kommer också att producera och vara mottaglig för ett e-fält i induktorns plan.

figurerna 4-6 visar olika sätt att neutralisera omkretsströmmen. Figur 4 är den enklaste och har fördelen att returtråden kan läggas till efter att induktorn har köpts eller byggts.

Fig. 4. Omkretsström motverkas med en returledning. Tråden är vit och löper mellan den yttre kanten av induktorn och den yttre delen av lindningen.

Fig. 5. Omkretsström motverkas med en returlindning.

Fig. 6. Omkretsström motverkas med en delad returlindning.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

det kommer att finnas en fördelning av potentialen längs lindningen. Detta kan leda till ett E-fält i toroidplanet och även en mottaglighet för ett e-fält i toroidplanet som visas i Figur 7. Detta kan mildras genom att använda en returlindning som visas på Figur 8. Med denna lindning, varje plats lindningen korsar sig, de två delarna kommer att vara lika och motsatt polaritet vilket väsentligen minskar e-fältet som genereras i planet.

Toroidal induktor / transformator och magnetisk vektorpotentialedit

visar utvecklingen av den magnetiska vektorpotentialen runt en symmetrisk toroidal induktor.

se Feynman Kapitel 14 och 15 för en allmän diskussion om magnetisk vektorpotential. Se Feynman sida 15-11 för ett diagram över den magnetiska vektorpotentialen runt en lång tunn solenoid som också uppvisar total inre inneslutning av B-fältet, åtminstone i den oändliga gränsen.

a-fältet är korrekt när antagandet b f a = 0 {\displaystyle bf{a}=0}

. Detta skulle vara sant under följande antaganden:

• 1. Coulomb-mätaren används
• 2. Lorenz-mätaren används och det finns ingen fördelning av laddningen, 0 {\displaystyle \rho = 0\,}
  
• 3. Lorenz-mätaren används och nollfrekvens antas
• 4. Lorenz-mätaren används och en icke-nollfrekvens som är tillräckligt låg för att försumma 1 c 2 oc t {\displaystyle {\frac {1}{c^{2}}}{\frac {\partial \Phi }{\partial t}}}
  

  antas.

nummer 4 kommer att antas för resten av detta avsnitt och kan hänvisas till ”kvasistatiskt tillstånd”.

även om den axiellt symmetriska toroidala induktorn utan omkretsström helt begränsar B-fältet i lindningarna, är A-fältet (magnetisk vektorpotential) inte begränsat. Pil # 1 på bilden visar vektorpotentialen på symmetriaxeln. Radiella strömsektioner a och b är lika avstånd från axeln men pekade i motsatta riktningar, så de kommer att avbryta. På samma sätt avbryter segmenten c och d. Faktum är att alla radiella nuvarande segment avbryter. Situationen för axiella strömmar är annorlunda. Den axiella strömmen på utsidan av toroiden pekas ner och den axiella strömmen på insidan av toroiden pekas upp. Varje axiellt strömsegment på utsidan av toroiden kan matchas med ett lika men motsatt riktat segment på insidan av toroiden. Segmenten på insidan är närmare än segmenten på utsidan till axeln, därför finns det en netto uppåtgående komponent i A-fältet längs symmetriaxeln.

representerar den magnetiska vektorpotentialen (a), magnetiskt flöde (B) och strömtäthet (j) fält runt en toroidal induktor med cirkulärt tvärsnitt. Tjockare linjer indikerar fältlinjer med högre medelintensitet. Cirklar i tvärsnitt av kärnan representerar B-flöde som kommer ut ur bilden. Plustecken på det andra tvärsnittet av kärnan representerar B-flöde som går in i bilden. Div a = 0 har antagits.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. 0 {\displaystyle {\frac {\partial e}{\partial t}}\rightarrow 0}

) har samma form, då linjerna och konturerna i A relaterar till B som linjerna och konturerna i B relaterar till j. således, en skildring av A-fältet runt en slinga av B-flöde (som skulle produceras i en toroidal induktor) är kvalitativt densamma som B-fältet runt en strömslinga. Figuren till vänster är en konstnärs skildring av A-fältet runt en toroidal induktor. De tjockare linjerna indikerar vägar med högre medelintensitet (kortare vägar har högre intensitet så att vägintegralet är detsamma). Linjerna dras bara för att se bra ut och ge a-fältets allmänna utseende.

Toroidtransformatorverkan i närvaro av totalt B-fält inneslutningredigera

e-och B-fälten kan beräknas från A-och XXL {\displaystyle \phi \,}

(skalär elektrisk potential) fält B = XXL a . {\displaystyle \ mathbf {B} =\nabla \ times \ mathbf {a} .}

och : e = − 2BL − 2BL A 2BL t {\displaystyle \mathbf {E} =-\nabla \Phi -{\frac {\partial \mathbf {A} }{\partial t}}

och så även om regionen utanför lindningarna saknar B-fält, är den fylld med icke-noll e-fält. Kvantiteten 0 {\displaystyle {\frac {\partial \mathbf {a} }{\partial t}}}

är ansvarig för den önskvärda magnetfältkopplingen mellan primär och sekundär medan kvantiteten 2 {\displaystyle \nabla \Phi \,}

är ansvarig för den oönskade elektriska fältkopplingen mellan primär och sekundär. Transformatordesigners försöker minimera den elektriska fältkopplingen. För resten av detta avsnitt antas att det är noll om inte annat anges.

Stokes sats gäller, så att vägintegralet för A är lika med det inneslutna B-flödet, precis som vägintegralet B är lika med en konstant gånger den inneslutna strömmen

vägintegralet för E längs sekundärlindningen ger sekundärens inducerade EMF (Elektro-motivkraft).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

vilket säger att EMF är lika med tidsförändringshastigheten för B-flödet som omges av lindningen, vilket är det vanliga resultatet.

Toroidal transformator Poynting vektor koppling från primär till sekundär i närvaro av totalt B fält inneslutningredigera

i denna figur, blå prickar indikerar var b-flöde från primärströmmen kommer ut ur bilden och plustecken indikerar var den går in i bilden.

förklaring av figureEdit

denna figur visar Halvdelen av en toroidtransformator. Kvasistatiska förhållanden antas, så fasen för varje fält är överallt densamma. Transformatorn, dess lindningar och alla saker fördelas symmetriskt kring symmetriaxeln. Lindningarna är sådana att det inte finns någon omkretsström. Kraven är uppfyllda för fullständig intern inneslutning av B-fältet på grund av primärströmmen. Kärnan och primärlindningen representeras av den gråbruna torusen. Primärlindningen visas inte, men strömmen i lindningen vid tvärsnittsytan visas som guld (eller orange) ellipser. B-fältet som orsakas av primärströmmen är helt begränsat till det område som omges av primärlindningen (dvs. kärnan). Blå prickar på vänstra tvärsnittet indikerar att linjer med B-flöde i kärnan kommer ut ur vänstra tvärsnittet. På det andra tvärsnittet indikerar blå plustecken att b-flödet kommer in där. E-fältet som kommer från de primära strömmarna visas som gröna ellipser. Sekundärlindningen visas som en brun linje som kommer direkt ner symmetriaxeln. I normal praxis är de två ändarna av sekundären förbundna med en lång tråd som håller sig långt borta från torusen, men för att upprätthålla den absoluta axiella symmetrin förutses hela apparaten vara inuti en perfekt ledande sfär med sekundärtråden ”jordad” på insidan av sfären i varje ände. Den sekundära är gjord av motståndstråd, så det finns ingen separat belastning. E-fältet längs sekundären orsakar ström i sekundären (gula pilar) som orsakar ett B-fält runt sekundären (visas som blå ellipser). Detta B-fält fyller utrymme, inklusive inuti transformatorkärnan, så i slutändan finns det kontinuerligt icke-noll B-fält från primär till sekundär, om sekundären inte är öppen kretsad. Korsprodukten Från e-fältet (kommer från primära strömmar) och B-fältet (kommer från sekundära strömmar) bildar Poynting-vektorn som pekar från det primära mot det sekundära.