en integrerad del av vätskedynamiken är vorticitet. Heuristiskt mäter den den lokala rotationen av ett vätskepaket. För fasta föremål talar vi inte om ett objekts vorticitet utan hänvisar istället till dess vinkelhastighet. Dessa två begrepp är relaterade men vorticitet är mer användbar när man diskuterar roterande föremål som deformeras, som en vätska gör.

vorticiteten hos ett givet hastighetsfält inom ett givet plan beräknas genom att välja två ortogonala axlar i det planet och lägga till vinkelhastigheten för varje axel. I ett fast föremål, eller en vätska som roterar som ett fast föremål (passande namnet fast kroppsrotation), är vorticiteten dubbelt vinkelhastigheten eftersom varje axel roterar i samma takt. Men i en vätska kan de två axlarna rotera i mycket olika hastigheter och till och med olika riktningar! Det är även möjligt att varje axel kan rotera men netto vorticiteten är noll (se irrotational vortex).

om rörelsen hos en vätska är strikt begränsad till att ligga i ett plan, tas vorticitetsvektorn att vara ortogonal mot planet och kan inte ändra riktningar (eller luta). Den enda aspekten av vorticiteten som kan förändras är dess storlek. Man tror att denna överföring av energi till större skalor är kopplad till bildandet av den stora röda fläcken på Jupiter.

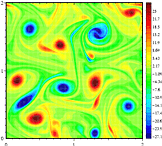
i tredimensionell fluidrörelse är vorticitetsvektorn tredimensionell genom att den har komponenter parallella med varje axel, x, y och z: z-komponenten är parallell med z-axeln och beskriver rotationshastigheten i xy-planet. Det är på grund av denna dikotomi att det finns en kvalitativ skillnad i beteende mellan tvådimensionell turbulens och tredimensionell turbulens. I det förra finns det en tendens för virvlar att klumpa ihop sig och bilda större virvlar, medan i det senare slits de vortiska rörelserna isär och energin kaskader ner till de minsta skalorna där den sedan diffunderas bort.

matematiskt är vorticiteten för ett givet hastighetsfält,

definieras som krökningen av hastighetsfältet och betecknas vanligtvis med den grekiska bokstaven omega,

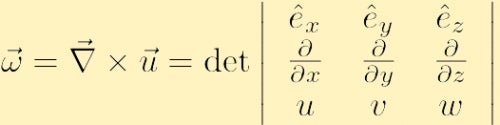
där vi har använt den konventionella nabla-symbolen för lutningen:

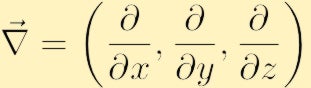
i komponentform hittas vorticiteten genom att expandera determinanten ovan,

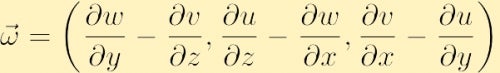
en annan viktig aspekt av vätskedynamik som är relaterad till vorticitet är cirkulation. Till skillnad från vorticitet som är en lokal egenskap, definierad vid varje punkt i rymden, är cirkulationen en global egenskap, definierad genom att integrera en egenskap hos vätskan över en kurva. I synnerhet, om du väljer någon sluten kontur och betecknar den med bokstaven C(t) är cirkulationen runt C(T), moturs, en skalär kvantitet betecknad med,

definieras som,

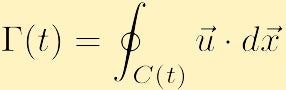
som kan vara en funktion av tiden, liksom den slutna konturen.

Låt oss ta en stund att förklara vad detta säger fysiskt. Vid varje punkt på konturen(t) hittar vi komponenten i hastigheten som är tangent till kurvan och multiplicerar denna skalär med en oändlig längd; projicera hastigheten på tangenten kommer nödvändigtvis att ge en storlek mellan hastigheten vid den positionen och noll. Om hastigheten är tangent till kurvan då får vi plus eller minus hastigheten på, om hastigheten är ortogonal till kurvan, vi får noll. Sedan integrerar vi denna kvantitet, ett annat sätt att säga att summera ett oändligt antal saker, runt konturen så att vi lägger till bidraget från varje punkt. Från detta konstaterar vi att cirkulationen längs en kontur C (t) är mängden flöde runt konturen (t); ett positivt eller negativt resultat motsvarar konturen medurs respektive medurs cirkulation. Ett extremt fall är där hastighetsfältet är överallt vinkelrätt mot kurvan C (t) och följaktligen finns det ingen cirkulation eftersom flödet alltid passerar konturen och aldrig flyter längs konturen. För att få en icke-nollcirkulation måste det finnas någon del av kurvan där flödet ligger längs den slutna konturen.

om hastighetsfältet är smidigt och det inte finns några singulariteter inom C(t) kan vi använda Stokes Integralteorem från vektorkalkyl för att skriva om cirkulationen som,

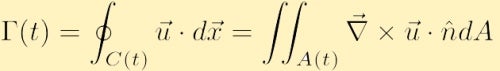
där A är området som finns i konturen C och XHamster är enhetens normala vektor till areaA.

innan vi överväger denna nya ekvation för cirkulationen är det användbart att förstå den fysiska betydelsen för Stokes sats där vektorfältet är hastigheten. I den dubbla integralen ovan beräknar vi vorticiteten vid varje punkt i konturen och summerar sedan vorticiteten över alla dessa punkter i A(t). I den enda integralen över den slutna konturen beräknar vi flödet längs områdets gräns. Stokes sats säger sedan att dessa kvantiteter är lika, och därmed att om det finns Genomsnittlig vorticitet inom ett område, vilket då måste betyda att området har en icke-noll rotationshastighet, måste det följaktligen finnas en nettocirkulation längs omkretsen av den gränsen.

från kalkylens Medelvärdessats kan vi ersätta integrand i dubbelintegralet med ett medelvärde, vilket motsvarar medelkomponenten i vorticiteten ortogonal till planet där C(t) ligger. Således är den andra tolkningen av cirkulationen att det är den genomsnittliga vorticitetstiden det område som finns inom C(t). Istället för att beräkna cirkulationen på den slutna konturen C(t) kan vi beräkna den genomsnittliga vorticiteten normal till A(t) och multiplicera den med området inom. Om du överväger det speciella fallet där vorticiteten är överallt konstant skulle cirkulationen vara storleken på vorticity gånger området som finns inom.

en punktvirvel är en virvel som inte har något område, vilket innebär att vorticitet endast är närvarande vid en enda punkt. För att studera punktvorter antar vi först att vi har ett 2D-inkompressibelt flöde. (Punktvirvlar kallas också ibland linjevirvlar när de ses i 3D.)

Efter några beräkningar bestämmer vi att hastighetsfältet som genereras av en punktvirvel, i komplex form, som ligger vid z0 ges av (där Gamma noll är cirkulationen runt punktvirveln, som ofta kallas styrkan hos punktvirveln):

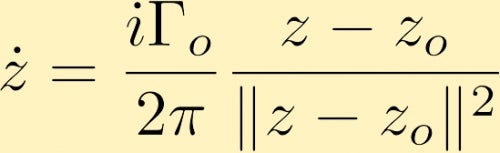
hastighetsfältet som genereras av en punktvirvel kan orsaka att en annan punktvirvel rör sig. Här är några exempel på detta: De två punktvirvlarna, både positiva och av samma storlek, de två punktvirvlarna, båda positiva men en har tredubbla styrkan hos den andra och en punktvirvel är negativ med dubbelt så stor som den andra som är positiv . En annan möjlighet är att överväga två punktvirvlar av samma storlek men motsatt tecken.

detta kan utökas till valfritt antal punktvirvlar, N. rörelsens ekvation i komplex form för en punktvirvel alfa ges av:

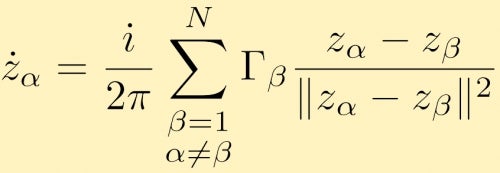
att titta på växelverkan mellan punktvorter är ett mycket intressant problem som är svårt att göra analytiskt, särskilt när antalet punktvorter ökar. Numeriska simuleringar av punktvortexinteraktioner är således mycket vanliga. En användbar tillämpning av stora punkt vortex simuleringar är om man tittar på stora kluster av punkt virvlar som simulerar virvlar med ändligt område. Här är beskrivningar och resultaten av flera stora punktvirvelsimuleringar. I det här fallet har vi två stora kluster av punktvorter med lika styrka sammanslagning. I nästa fall börjar vi med en ring av klustrade punktveraciteter.

för att hitta en ekvation för vorticitetens utveckling börjar vi med momentum ekvationen. I momentumekvationen kan den advektiva termen skrivas om enligt följande,

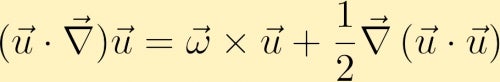
vi beräknar nästa curl av momentum ekvationen och genom vissa vektoridentiteter får vi vorticitetsekvationen:

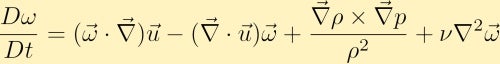
vorticitetsekvationen visar hur vorticitet kan genereras i en vätska. Utan förlust av generalitet antar vi att vi ursprungligen bara har vorticitet i z-riktningen. Från detta kan vi se hur var och en av de fyra olika termerna kan förändra vorticiteten.

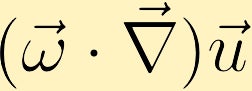
om det finns en förändring i hastighet med riktning av befintlig vorticitet kan vorticitet genereras.

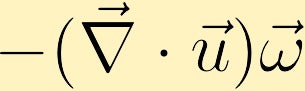
om ett fluidpaket expanderar och vorticiteten är positiv kommer vorticiteten hos fluidpaketet att minska och om paketet kontraherar kommer vorticiteten att öka.

vätskeskikt med konstant densitet (isopycnals) vill sammanfalla med lager med konstant tryck (isobars). Om dessa lager inte sammanfaller börjar vätskan att rotera för att få dem att ställa upp vilket gör att vorticitet genereras. (I exemplet börjar vi med noll vorticitet.)

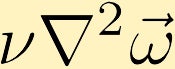
viskösa krafter orsakar diffusion av vorticitet. (I exemplet börjar vi med en punkt med oändlig vorticitet i mitten.)