een integraal onderdeel van de vloeistofdynamica is vorticity. Heuristisch meet het de lokale rotatie van een vloeibaar perceel. Voor vaste objecten spreken we niet van de vorticiteit van een object, maar in plaats daarvan verwijzen we naar zijn hoeksnelheid. Deze twee concepten zijn gerelateerd, maar vorticiteit is nuttiger bij het bespreken van roterende objecten die vervormen, zoals een vloeistof doet.

De vorticiteit van een gegeven snelheidsveld binnen een gegeven vlak wordt berekend door twee orthogonale assen in dat vlak te kiezen en de hoeksnelheid van elke as op te tellen. In een vast object, of een vloeistof die roteert als een vast object (toepasselijk solid body rotation genoemd), is de vorticiteit tweemaal de hoeksnelheid omdat elke as met dezelfde snelheid roteert. Echter in een vloeistof kunnen de twee assen draaien op zeer verschillende snelheden en zelfs verschillende richtingen! Het is zelfs mogelijk dat elke as kan draaien maar de netto vorticiteit is nul (zie irrotationele vortex).

als de beweging van een vloeistof strikt beperkt is tot het liggen in een vlak, wordt de vorticiteitsvector als loodrecht op het vlak beschouwd en kan de richting (of kanteling) niet veranderen. Het enige aspect van de vorticiteit dat kan veranderen is de omvang ervan. Er wordt aangenomen dat deze overdracht van energie naar grotere schalen verbonden is met de vorming van de grote rode vlek op Jupiter.

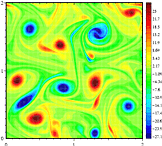
in driedimensionale vloeistofbeweging is de vorticiteitsvector driedimensionaal in die zin dat hij componenten heeft die evenwijdig zijn aan elke as, x, y en z: de Z-component is evenwijdig aan de Z-as en beschrijft de rotatiesnelheid in het xy-vlak. Door deze tweedeling is er een kwalitatief verschil in gedrag tussen tweedimensionale turbulentie en driedimensionale turbulentie. In de eerste is er een neiging voor vortices om samen te klonteren en grotere vortices te vormen, terwijl in de tweede de vorticale bewegingen uit elkaar worden gescheurd en de energie cascades tot op de kleinste schalen waar het vervolgens wordt verspreid.

wiskundig wordt de vorticiteit van een gegeven snelheidsveld,

gedefinieerd als de krul van het snelheidsveld, en wordt meestal aangeduid met de Griekse letter omega,

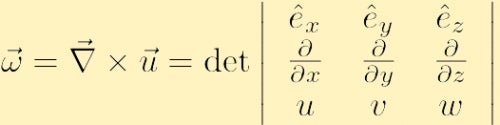
waar we het conventionele Nabla symbool voor de gradiënt hebben gebruikt:

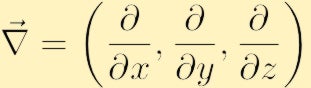
in componentvorm wordt de vorticiteit gevonden door de determinant hierboven uit te breiden,

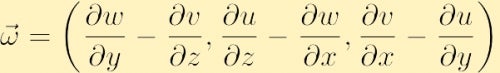
een ander belangrijk aspect van de vloeistofdynamica dat gerelateerd is aan vorticiteit is circulatie. In tegenstelling tot vorticity, een lokale eigenschap, die op elk punt in de ruimte wordt gedefinieerd, is circulatie een globale eigenschap, gedefinieerd door het integreren van een eigenschap van de vloeistof over een kromme. In het bijzonder, als je een gesloten contour kiest en deze aanduidt met de letter C(t), is de circulatie rond C(t), in een richting tegen de klok in, een scalaire hoeveelheid aangegeven met,

wordt gedefinieerd als,

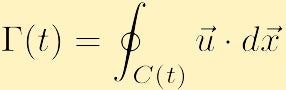
die kan zijn een functie van de tijd, net als de gesloten contour.

laten we een moment nemen om uit te leggen wat dit fysiek zegt. Op elk punt van de contourC(t) vinden we de component van de snelheid die raaklijnt aan de kromme en vermenigvuldigen we deze scalar met een oneindig kleine lengte; het projecteren van de snelheid op de raaklijn zal noodzakelijkerwijs een magnitude geven tussen de snelheid op die positie en nul. Als de snelheid raaklijnt aan de kromme dan krijgen we plus of min De snelheid van, als de snelheid orthogonaal is aan de kromme, krijgen we nul. Dan integreren we deze hoeveelheid, een andere manier om een oneindig aantal dingen op te tellen, rond de contour zodat we de bijdrage van elk punt toevoegen. Hieruit kunnen we vaststellen dat de circulatie langs een contour C (t)de hoeveelheid stroom rond de contourC(t) is; een positief of negatief resultaat komt overeen met de omtrek respectievelijk met de klok mee circulatie. Een extreem geval is waar het snelheidsveld overal loodrecht staat op de kromme C (t) en er dus geen circulatie is omdat de stroming altijd de contour kruist en nooit langs de contour stroomt. Om een niet-nul circulatie te krijgen moet er een deel van de curve zijn waar de stroom langs de gesloten contour is.

als het snelheidsveld glad is en er geen singulariteiten zijn binnen C(t) dan kunnen we Stokes’ Integraalstelling uit de vectorcalculus gebruiken om de circulatie te herschrijven als,

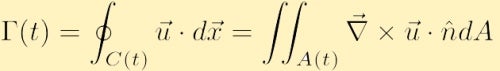
waar A het gebied is dat zich binnen de contour C bevindt en de eenheidsnormale vector naar het gebied is.

voordat we deze nieuwe vergelijking voor de circulatie bekijken, is het nuttig om de fysische betekenis voor de Stelling van Stokes te begrijpen, waar het vectorveld de snelheid is. In de dubbele integraal hierboven berekenen we de vorticiteit op elk punt binnen de contour en vatten dan de vorticiteit op over al deze punten in A(t). In de enkele integraal over de gesloten contour berekenen we de stroom langs de grens van het gebied. De stelling van Stokes stelt dan dat deze grootheden gelijk zijn, en dus dat als er een gemiddelde vorticiteit binnen een gebied is, wat dan moet betekenen dat het gebied een niet-nulrotatiesnelheid heeft, er dus een nettocirculatie langs de omtrek van die grens moet zijn.

van de gemiddelde waardestelling van de calculus kunnen we de integrand in de dubbele integraal vervangen door een gemiddelde waarde, die overeenkomt met de gemiddelde component van de vorticiteit orthogonaal aan het vlak waarin C(t) ligt. De tweede interpretatie van de circulatie is dus dat het de gemiddelde vorticiteit maal het gebied binnen C(t) is. In plaats van het berekenen van de circulatie op de gesloten contour C(t) kunnen we de gemiddelde vorticiteit normaal berekenen tot A(t) en vermenigvuldigen met de oppervlakte binnen. Als je kijkt naar het speciale geval waar de vorticiteit overal constant is, zou de circulatie de grootte zijn van de vorticiteit maal het gebied binnen.

een puntvortex is een vortex die geen oppervlakte heeft, wat betekent dat vorticiteit slechts aanwezig is op een enkel punt. Om puntwervels te bestuderen zullen we eerst aannemen dat we een 2D-niet-drukbare stroom hebben. (Puntvortices worden ook wel lijnvortices genoemd wanneer ze in 3D worden bekeken.)

na enkele berekeningen bepalen we dat het snelheidsveld dat wordt gegenereerd door een puntvortex, in complexe vorm, dat zich op z0 bevindt, wordt gegeven door (waarbij Gamma nul de circulatie is rond de puntvortex, die vaak wordt aangeduid als de sterkte van de puntvortex):

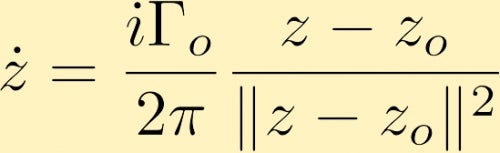
Het snelheidsveld dat door een puntvortex wordt gegenereerd, kan een andere puntvortex laten bewegen. Hier zijn een paar voorbeelden van deze: De tweepuntsvortices, zowel positief als van gelijke grootte, de tweepuntsvortices, beide positief, maar de ene heeft drie keer de sterkte van de andere en de ene puntvortex is negatief met twee keer de grootte van de andere die positief is . Een andere mogelijkheid is om twee puntwervels van dezelfde grootte maar tegenovergestelde teken te overwegen.

Dit kan worden uitgebreid tot een willekeurig aantal puntvortices, N. de vergelijking van beweging in complexe vorm voor een puntvortex alfa wordt gegeven door:

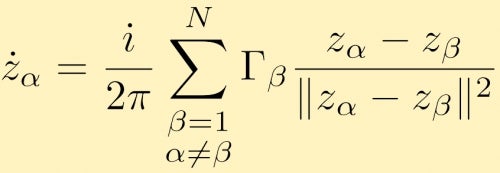
kijken naar de interacties van puntwervels is een zeer interessant probleem dat moeilijk analytisch te doen is, vooral omdat het aantal puntwervels toeneemt. Numerieke simulaties van puntvortex interacties is dus zeer gebruikelijk. Een nuttige toepassing van grote punt vortex simulaties is als je kijkt naar grote clusters van punt vortices die vortices simuleert met eindige oppervlakte. Hier zijn beschrijvingen en de resultaten van verschillende grote punt vortex simulaties. In dit geval hebben we twee grote clusters van puntwervels van gelijke sterkte die samensmelten. In het volgende geval beginnen we met een ring van geclusterde puntverkeuringen.

om een vergelijking te vinden voor de evolutie van de vorticiteit beginnen we met de momentumvergelijking. In de momentumvergelijking kan de advectieve term als volgt worden herschreven,

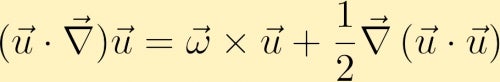
we berekenen vervolgens de krul van de momentumvergelijking en door enkele vectoridentiteiten krijgen we de vorticiteitsvergelijking:

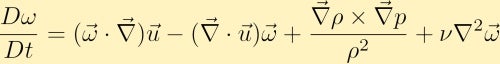
De vorticiteitsvergelijking laat zien hoe vorticiteit kan worden gegenereerd in een vloeistof. Zonder verlies van algemeenheid zullen we aannemen dat we aanvankelijk alleen vorticiteit in de z-richting hebben. Hieruit kunnen we zien hoe elk van de vier verschillende termen de vorticiteit kan veranderen.

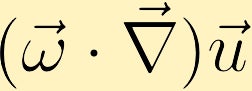
als er een verandering is in de snelheid met de richting van de bestaande vorticiteit, kan vorticiteit worden gegenereerd.

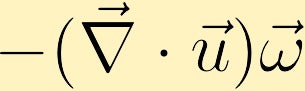
als een vloeibaar pakket uitdijt en de vorticiteit positief is, zal de vorticiteit van het vloeibare pakket afnemen en als het pakket samentrekt, zal de vorticiteit toenemen.

vloeibare lagen met constante dichtheid (isopycnalen) willen samenvallen met lagen met constante druk (isobars). Als deze lagen niet samenvallen de vloeistof beginnen te draaien om ze line-up waardoor vorticity worden gegenereerd. (In het voorbeeld beginnen we met nul vorticity.)

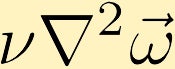
viskeuze krachten veroorzaken de diffusie van vorticiteit. (In het voorbeeld beginnen we met een punt van oneindige vorticiteit in het centrum.)