In het tijdperk van de digitale wereld, zien we aanbeveling op elk gebied weer het is e-commerce website of entertainment website of sociale netwerksites. Aanbeveling geeft niet alleen de gebruiker zijn aanbevolen keuze (op basis van eerdere activiteit), maar het vertelt ook over het gedrag van de gebruiker (sentimentele analyse of emotie AI).

dus eerst, laten we begrijpen wat aanbeveling is. Het is in principe aan te bevelen item aan de gebruiker op basis van zijn verleden zoeken/activiteit.

figuur 1 vertelt de aanbeveling van Amazon op basis van de browsegeschiedenis in het verleden en de zoekopdrachten in het verleden. We kunnen zeggen dat aanbeveling in principe toekomstig gedrag voorspelt op basis van gedrag uit het verleden. Er zijn twee soorten benaderingen die worden gebruikt in het aanbevelingssysteem

1-Content Based Filtering

2 – Collaborative based filtering

Content Based Filtering-

Het is gebaseerd op het idee om het item aan gebruiker K aan te bevelen dat vergelijkbaar is met het vorige item dat hoog wordt beoordeeld door K. basisconcept in content based filtering is TF-IDF (Term frequency — inverse document frequency), dat wordt gebruikt om het belang van document/word / movie enz.te bepalen. Content based filtering toont transparantie in Aanbeveling, maar in tegenstelling tot collaborative filtering kan het niet efficiënt werken voor grote data

Collaborative based filtering

Het is gebaseerd op het idee dat mensen die dezelfde interesse hebben in bepaalde soorten items ook dezelfde interesse zullen delen in een ander soort items, in tegenstelling tot content based die in principe vertrouwen op metagegevens terwijl het gaat om echte activiteit. Dit type van filtering is flexibel voor het grootste deel van het domein (of we kunnen zeggen dat het domeinvrij is) maar vanwege het probleem met koude start, wordt data sparsity (die werd behandeld door matrix factorisatie) dit type algoritme geconfronteerd met een tegenslag in een scenario.

Matrix factorization

Matrix factorization komt in de schijnwerpers na Netflix competition (2006), toen Netflix een prijzengeld van $1 miljoen aankondigde aan degenen die de root mean square performance met 10% zullen verbeteren. Netflix heeft een trainingsset van 100,480,507 beoordelingen verstrekt die 480,189 gebruikers aan 17,770 films hebben gegeven.

Matrix-factorisatie is de collaboratieve filtermethode waarbij matrix m * n wordt ontleed in m * k en k * n . Het wordt in principe gebruikt voor de berekening van complexe matrix operatie. De verdeling van de matrix is zodanig dat als we gefactoriseerde matrix vermenigvuldigen we de originele matrix krijgen zoals getoond in Figuur 2. Het wordt gebruikt voor het ontdekken van latente kenmerken tussen twee entiteiten (kan voor meer dan twee entiteiten worden gebruikt, maar dit valt onder tensor factorisatie)

Matrixdecompositie kan worden ingedeeld in drie type-

1 – LU decompositie — decompositie van matrix in L-en U-matrix waarbij L de onderste driehoekige matrix is en U de bovenste driehoekige matrix, meestal gebruikt voor het bepalen van de lineaire regressiecoëfficiënt. Deze ontleding is mislukt als matrix niet gemakkelijk kan zijn ontleed

2 – QR matrix ontleding-ontleding van matrix in Q en R waarbij Q Is vierkante matrix en R is bovenste driehoekige matrix (niet noodzakelijk vierkant). Gebruikt voor eigen systeemanalyse

3 – Cholesky decompositie-Dit is de meest gebruikte decompositie in machine learning. Gebruikt voor het berekenen van lineaire kleinste kwadraat voor lineaire regressie

Matrix factorisatie kan worden gebruikt in verschillende domeinen zoals beeldherkenning, aanbeveling. Matrix gebruikt in dit soort problemen zijn over het algemeen schaars, omdat er kans is dat een gebruiker slechts een aantal films kan beoordelen. Er zijn verschillende toepassingen voor matrixfactorisatie zoals Dimensionaliteitsreductie (om meer te weten te komen over dimensionaliteitsreductie, zie Curse Of Dimensionality), latente waardedecompositie

Probleemstatement

in Tabel 1 hebben we 5 gebruikers en 6 films waar elke gebruiker elke film kan beoordelen. Zoals we kunnen zien dat Henry niet beoordeelde voor Thor en Rocky op dezelfde manier Jerry niet beoordeelde voor Avatar. In de echte wereld scenario van deze soorten matrix kan zeer sparse matrix

Onze probleemstelling is dat we hebben bij het vinden van beoordelingen voor niet-geclassificeerde films zoals weergegeven in Tabel 1

Als ons doel te vinden rating van de gebruiker door matrix ontbinding maar voordat dat we moeten gaan door middel van Singuliere waarden Decompositie (SVD) omdat de matrix ontbinding en SVD zijn aan elkaar gerelateerd

SVD en Matrix factorisatie

voordat u naar de diepte van SVD gaat, kunt u eerst begrijpen wat K is en(K) transponeren. Als we PCA uitvoeren op matrix K (Tabel 1) krijgen we alle gebruikersvector. Later kunnen we deze vectoren in kolom van matrix U plaatsen en als we PCA uitvoeren op transpose (K) krijgen we alle filmvector die kolom worden voor matrix M.

dus in plaats van PCA op K en transpose(K) afzonderlijk uit te voeren, kunnen we SVD gebruiken die PCA op K kan uitvoeren en transpose(K) in een enkele opname. SVD is in principe gefactoriseerd matrix K in matrix U, matrix M en diagonale matrix:

waarbij K is originele Matrix, u is gebruikersmatrix,m is filmmatrix en de middelste is diagonale matrix

omwille van de eenvoud kunnen we diagonale matrix een tijdje verwijderen dus nieuwe vergelijking wordt:

Let R is waardering gedefinieerd voor gebruiker u en item I, P is rij van M voor een gebruiker en q is de kolom van transponeren(u) voor een specifiek item I. :

Opmerking — Als K dichte matrix waarde dan M eigenvector van K*transpose(K), ook de waarde van U zal worden eigenvector van transpose(K)*K, maar onze matrix is sparse matrix kunnen we niet berekenen, U en M door deze aanpak

hier is Dus onze taak is het vinden van matrix M en U . Een manier is om willekeurige waarde te initialiseren naar M en U en te vergelijken met de originele Matrix K als de waarde dicht bij K ligt dan de procedure te stoppen anders minimaliseert u en M totdat ze dicht bij K zijn . Het proces van deze optimalisatie heet gradiëntafdaling

dus onze basistaak is het minimaliseren van de gemiddelde kwadraat fout functie die kan worden weergegeven als :

As our main task is to minimize the error i.e. we hebben om te vinden in welke richting we moeten gaan voor dat we hebben om het te onderscheiden, vandaar dat nieuwe vergelijking

Vandaar de bijgewerkte waarde voor p en u zal nu worden:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Op basis van die beslissingsregel kunnen we de verdeling van gegevens onderscheiden

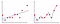
in figuur 2 is het eerste perceel waar het model lineair is aangebracht, terwijl het op het tweede perceel is uitgerust met een polynomiale graad. Op het eerste gezicht lijkt het erop dat het tweede perceel veel beter is dan het eerste perceel omdat het 99% nauwkeurigheid geeft op trainingsgegevens, maar wat als we testgegevens invoeren en het geeft 50% nauwkeurigheid op testgegevens . Dit soort problemen wordt overbevissing genoemd en om dit probleem op te lossen introduceren we een concept dat regularisatie heet.

aangezien het probleem van overbevissing vaak voorkomt bij machine learning, zijn er twee soorten regularisatiebenadering die kunnen worden gebruikt om de overbevissing

1 – L1 – regularisatie

2-L2-regularisatie

L1-regularisatie toe te voegen lineaire grootte van de coëfficiënt als strafterm, terwijl in L2 het vierkante magnitude van de coëfficiënt toe te voegen aan de loss function/error function (zoals hierboven besproken). L1 retourneert schaarse matrices terwijl L2 dat niet doet. L1 regularisatie werkt goed in functie Selectie in schaarse matrix.

In de dataset van de aanbeveling zijn er ook grote kansen op overbevissing van gegevens. Dus, om het overfitting probleem kunnen we toevoegen L2 regularisatie (als matrix is al schaars we niet nodig L1 regularisatie hier)in verlies functie dus nieuwe vergelijking van verlies functie zal zijn:

Opnieuw vinden we gradiënt bijgewerkt op MSE en bijgewerkt te krijgen punten door het volgen van dezelfde methode als hierboven besproken

Een belangrijk ding om te overwegen in het bovenstaande scenario de matrix P en Q zijn niet-negatief, dus deze types van ontbinding is ook de zogenaamde niet-negatieve ontbinding. Als niet-negatieve factorisatie automatisch extraheert informatie voor niet-negatieve set van vector. NMF wordt veel gebruikt in beeldverwerking ,tekst mining, analyse van hoogdimensionale data