Antény vyzařovat Elektromagnetické energie, přenášet nebo přijímat informace. Proto jsou pojmy energie a síla spojeny s těmito elektromagnetickými vlnami a musíme o nich diskutovat. Elektromagnetická vlna má elektrické i magnetické pole.

zvažte vlnu v každém okamžiku, kterou lze zobrazit v obou vektorech. Následující obrázek ukazuje znázornění složek elektrického a magnetického pole v elektromagnetické vlně.

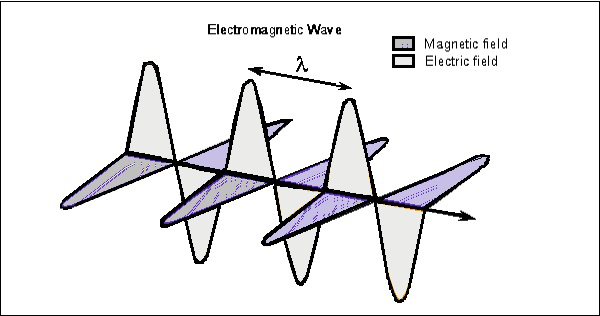
elektrická vlna je přítomna vertikálně k šíření em vlny, zatímco magnetická vlna je vodorovně umístěna. Obě pole jsou v pravém úhlu k sobě.

Poyntingova Vektoru

Poyntingova vektoru popisuje energii elektromagnetické Vlny za jednotku času na jednotku plochy v daném časovém okamžiku. John Henry Poynting poprvé odvodil tento vektor v roce 1884, a proto byl pojmenován po něm.

Definice − „Poyntingova vektoru udává rychlost přenosu energie na jednotku plochy“

nebo

„energie, které vlna nese za jednotku času na jednotku plochy je dán Poyntingova vektoru.“

poyntingův vektor je reprezentován Ŝ.

jednotky

si jednotka poyntingova vektoru je W / m2.

Matematický Výraz

množství, které se používá k popisu energie spojené s elektromagnetické vlny je okamžitá Poyntingova vektoru, který je definován jako

$$\hat{S} = \hat{E} \times \hat{H}$$

, Kde

• $\hat{S}$ je okamžitá Poyntingova vektoru (W/m2).

• $\hat{E}$ je okamžitá intenzita elektrického pole (V / m).

• $\hat{H}$ je okamžitá intenzita magnetického pole (A / m).

důležitým bodem, který je třeba poznamenat, je, že velikost E je větší než H V em vlně. Oba však přispívají stejným množstvím energie. Ŝ je vektor, který má směr i velikost. Směr Ŝ je stejný jako rychlost vlny. Jeho velikost závisí na E a H.

Odvození Poyntingova Vektoru

mít jasnou představu o Poyntingova vektoru, nechte nás projít odvození tohoto Poyntingova vektoru, v krok-za-krokem procesu.

představme si, že em vlna prochází oblastí (a) kolmou k ose X, podél které se vlna pohybuje. Při průchodu A, v nekonečném čase (dt), vlna cestuje vzdáleností (dx).

$$dx = C\ dt$$

, Kde

$$C = rychlost\\ světlo = 3\times 10^{8}m/s$$$$objemu, dv = Adx = AC\ dt$$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$$= \epsilon_{0} AC \ E^{2}\ dt$$

Proto, Energie převedeny v čase (dt) na části (A) je −

$$S = \frac{Energetika}{Time\times Oblasti} = \frac{dW}{dt\} = \frac{\epsilon_{0}ACE^{2}\ dt}{dt\} = \epsilon_{0}C\:E^{2}$$

, Protože

$$\frac{E}{H} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \ pak\ Y= \frac{CB^{2}}{\mu_{0}}$$

, Protože

$$C = \frac{E}{H} \ pak \ Y = \frac{EB}{\mu_{0}}$$$$= \klobouk{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Þ označuje Poyntingova vektoru.

výše uvedená rovnice nám dává energii za jednotku času na jednotku plochy v daném okamžiku, který se nazývá Poyntingův vektor.