Hranicích v Genetice
Úvod
Efektivní velikost populace (Ne) je důležitý genetický parametr, který odhaduje výši genetický drift v populaci, a byla popsána jako velikost idealizované Wright–Fisher populace očekává, že získá stejnou hodnotu dané genetické parametr jako ve zkoumané populace (Crow and Kimura 1970). Velikost Ne může být ovlivněna kolísáním velikosti populace sčítání lidu (Nc), poměrem pohlaví v chovu a rozptylem v reprodukční úspěšnosti.
ne odhad lze dosáhnout pomocí přístupů, které spadají do tří metodologických kategorií: demografické, rodokmenové nebo markerové (Flury et al ., 2010). Údaje o rodokmenu se tradičně používají k získání odhadů Ne u hospodářských zvířat. Spolehlivé odhady Ne však závisí na úplnosti rodokmenu. Tento stav znalostí je proveditelný u některých domácích populací, jejichž demografické parametry byly přesně sledovány po dostatečně velký počet generací. V praxi však použitelnost tohoto přístupu zůstává omezena na několik případů týkajících se vysoce řízených plemen (Flury et al ., 2010; Uimari a Tapio, 2011).
jedním z řešení, jak překonat omezení neúplného rodokmenu, je odhadnout nedávný trend v Ne pomocí genomických dat. Několik autorů uznalo, že Ne lze odhadnout z informací o vazebné nerovnováze (LD) (Sved, 1971; Hill, 1981). LD popisuje nenáhodnou asociaci alel v různých lokusech jako funkci rychlosti rekombinace mezi fyzickými pozicemi lokusů v genomu. Nicméně, LD podpisy mohou také důsledkem demografických procesů jako jsou příměsi a genetický drift (Wright, 1943; Wang, 2005), nebo prostřednictvím procesů jako „autostop“ v průběhu selektivního zametá (Smith a Haigh, 1974) nebo výběr pozadí (Olivy et al., 1997). V takových scénářích se alely na různých lokusech spojují nezávisle na jejich blízkosti v genomu. Za předpokladu, že populace je uzavřená a panmiktická, hodnota LD vypočtená mezi neutrálními nelinkovanými lokusy závisí výhradně na genetickém driftu (Sved, 1971; Hill, 1981). Tento výskyt lze použít k předpovědi Ne kvůli známému vztahu mezi rozptylem LD (vypočteným pomocí frekvencí alely) a efektivní velikostí populace (Hill, 1981).
nedávné pokroky v technologii genotypizace (např. pomocí SNP korálek pole s desítkami tisíc DNA sondy) umožnily sběr velkého množství genome-wide linkage dat ideální pro odhad Ne u hospodářských zvířat a člověka mezi ostatními (např. Tenesa et al., 2007; de Roos et al., 2008; Corbin a kol., 2010; Uimari a Tapio, 2011; Kijas a kol., 2012). Nicméně, software nástroj, který umožňuje odhad Ne z LD chybí, a vědci se v současné době spoléhají na kombinaci nástrojů pro manipulaci s daty, odvodit, LD, a mají tendenci používat zakázku skripty provádět příslušné výpočty a odhad Ne.
Zde popíšeme SNeP, softwarový nástroj, který umožňuje odhad Ne trendy celé generace pomocí SNP data, která opravuje pro velikost vzorku, fázování a rekombinační rychlost.
Materiály a Metody
metoda SNeP používá pro výpočet LD závisí na dostupnosti postupně údajů. Když fáze je známo, může uživatel vybrat Kopec a Robertson (1968) na druhou korelační koeficient, který využívá haplotyp frekvence definovat LD mezi každou dvojicí loci (Rovnice 1). Při absenci známé fáze však lze zvolit na druhou Pearsonův součin-momentový korelační koeficient mezi páry lokusů. I když tyto dva přístupy nejsou stejné ,jsou vysoce srovnatelné (McEvoy et al., 2011):
kde pA a pB jsou resp. frekvence alel a a B na dvou různých lokusech (X, Y) naměřených u n jedinců, pAB je frekvence haplotyp s alely a a B v populaci studováno, X a Y jsou průměrné genotypové frekvence pro první a druhé místo, respektive, Xi je genotyp jedince jsem na první místo a Yi je genotyp jedince jsem na druhé místo. Rovnice (2) koreluje genotypové alela počítá místo haplotyp frekvencí a není ovlivněn dvakrát heterozygoti (tento přístup vede ve stejné odhady jako –r2 možnost v PLINK).
SNeP odhady historické efektivní velikost populace na základě vztahu mezi r2, Ne, a c (rychlost rekombinace), (Rovnice 3—Sved, 1971), a umožňuje uživatelům, aby zahrnovala opravy za velikost vzorku a nejistota gametic phase (Rovnice 4—Weir a Hill, 1980):
, kde n je počet jednotlivých vzorků, β = 2, když gametic phase je známý a β = 1, pokud místo fázi není znám.
Několik aproximace se používají k odvození rekombinační rychlost pomocí fyzické vzdálenosti (δ) mezi dvěma loci jako referenční a překládat to do linkage vzdálenost (d), který je obvykle popisován jako Mb(δ) ≈ cM(d). Pro malé hodnoty d druhá aproximace je platný, ale pro větší hodnoty d pravděpodobnost více rekombinace a rušení se zvyšuje, navíc vztah mezi mapou vzdálenost a rychlost rekombinace není lineární, jako maximální rychlost rekombinace možné je 0,5. Pokud tedy nepoužíváme velmi krátké δ, aproximace d ≈ c není ideální (Corbin et al., 2012). Proto jsme implementována funkce mapování přeložit odhadované d do c po Haldane (1919), Kosambi (1943), Sved (1971), a Sved a Feldman (1973). Zpočátku SNeP vyvozuje, d pro každou dvojici Snp jako přímo úměrný δ podle d = kδ kde k je uživatelem definované rekombinace rychlost hodnota (výchozí hodnota je 10-8 jako v Mb = cM). Odvozená hodnota δ pak může být podrobena jedné z dostupných mapovacích funkcí, pokud to uživatel vyžaduje.
řešení rovnice (3) Pro Ne a včetně všech popsaných korekcí umožňuje predikci Ne z LD dat pomocí (Corbin et al., 2012):
kde Nt je efektivní velikost populace t generacemi vypočítá jako t = (2f(ct))-1 (Hayes et al., 2003), ct je rychlost rekombinace definované pro konkrétní fyzickou vzdálenost mezi markery a volitelně nastavit pomocí mapování funkce je uvedeno výše, r2adj je LD hodnota upravena na velikost vzorku a α:= {1, 2, 2.2} je korekce pro výskyt mutací (Ohta a Kimura, 1971). Proto, LD na větší rekombinantní vzdálenosti je informativní o nedávné Ne, zatímco kratší vzdálenosti poskytují informace o vzdálenějších časech v minulosti. Binning systém je implementován za účelem získání průměrných hodnot r2, které odrážejí LD pro specifické vzdálenosti mezi lokusy. Implementovaný systém binning používá následující vzorec k definování minimálních a maximálních hodnot pro každý bin:
Kde bi (ℕ1) je i-tý bin z celkového počtu popelnic (totBins), mysl, a maxD jsou, respektive minimální a maximální vzdálenost mezi Snp a x je kladné reálné číslo (ℝ0), Když se x rovná 1, rozdělení vzdáleností mezi zásobníky je lineární a každý koš má stejný dosah. U větších hodnot x se rozložení vzdáleností mění, což umožňuje větší rozsah na posledních koších a menší rozsah na prvních koších. Změna tohoto parametru umožňuje uživateli mít dostatečný počet párových srovnání, aby přispěl ke konečnému odhadu Ne pro každý zásobník.
ukázková Aplikace
testovali Jsme SNeP s dvou publikovaných souborů údajů, které byly dříve použity k popisu trendů v Ne v průběhu času pomocí LD, Bos indicus a Ovis aries . Odhady r2 pro datové sady skotu byly získány autory pomocí GenABLE (Aulchenko et al., 2007) s použitím minimální frekvenci alel (MAF) < 0,01 a nastavení rekombinační rychlost pomocí Haldane mapování funkce (Haldane, 1919). Odhady R2 údajů o ovcích byly vypočteny autory pomocí PLINK-1.07 (Purcell et al ., 2007), s MAF < 0.05 a bez dalších oprav. Pro oba autozomální datové sady R2 odhady, kde korigovány pro velikost vzorku pomocí rovnice (4)s β = 2. Pro tyto srovnávací analýzy SNeP příkazového řádku zahrnuta stejné parametry použité pro publikované údaje, na rozdíl od r2 odhady, vypočtené prostřednictvím genotyp počítat a použití SNeP román binning strategie.
Výsledky
SNeP je multithreaded aplikace vyvinutá v jazyce C++ a binárky pro většinu běžných operačních systémů (Windows, OSX a Linux) si můžete stáhnout ze https://sourceforge.net/projects/snepnetrends/. Binární soubory jsou doprovázeny příručkou popisující postupné použití SNeP k odvození trendů v Ne, jak je popsáno zde. SNeP produkuje výstup souboru s tabulátorem sloupce ukazuje následující pro každý bin, která byla použita k odhadu Ne: počet generací v minulosti, že bin odpovídá (např., Před 50 generacemi), odpovídající odhad Ne, průměrná vzdálenost mezi každou dvojicí SNP v koši, průměrná r2 a směrodatná odchylka r2 v koši a počet SNP použitých pro výpočet r2 v koši. Tento soubor lze snadno importovat do aplikace Microsoft Excel, R nebo jiného softwaru pro vykreslení výsledků. Zde zobrazené grafy (obrázky 1, 3) odpovídají sloupcům před generacemi a Ne z výstupního souboru. Sloupec s r2 směrodatná odchylka je k dispozici pro uživatele zkontrolujte, zda není rozptyl v Ne odhad v každé bin, zejména pro ty, koše odrážející starší odhady času a které jsou méně spolehlivé, jako je počet Snp používá k odhadu r2 se stává menší.
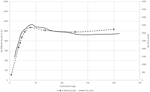
Obrázek 1. Srovnání Ne trendů šesti švýcarských plemen ovcí podle Burren et al. (2014) (přerušované čáry) a tato práce (plné čáry).
formát potřebný pro vstupní soubory je standardní formát PLINK (soubory ped a map) (Purcell et al., 2007). SNeP umožňuje uživatelům buď vypočítat LD na datech, jak je popsáno výše, nebo použít vlastní precalculated LD matici odhadnout Ne pomocí rovnice (5).
softwarové rozhraní umožňuje uživateli kontrolu všech parametrů analýzy, např. vzdáleností mezi Snp v bp, a sadu chromozomů použitých v analýze (např., 20-23). Navíc SNeP obsahuje možnost zvolit prahovou hodnotu MAF (výchozí 0.05), protože bylo prokázáno, že účetnictví pro MAF výsledky v nezkreslené r2 odhady bez ohledu na velikost vzorku (Sved et al., 2008). SNeP je vícevláknové architektura umožňuje rychlý výpočet velkých souborů dat (testovali jsme až do ~100K Snp na jeden chromozom), například BOS osobních údajů popsané zde byl analyzován s jedním procesorem v 2’43“, použití dvou procesorů sníží čas 1’43“, čtyři procesory sníží čas analýzy 1’05“.
Zebu Příklad
Pro zebu analýza, tvary Ne křivky získané s SNeP a jejich zveřejněných údajů trendů ukázal stejné trajektorii s plynulý pokles až kolem 150 generacemi, následuje expanze, s vrcholem kolem 40 generacemi a končí v prudkém poklesu na nejnovější generací (Obrázek 1). Nicméně, zatímco trendy v obou křivek byly stejné, dvou přístupů došlo v různých Ne odhady, s SNeP hodnoty jsou přibližně třikrát větší než v původní papírové. Zatímco jsme se pokusili použít autorů parametrů v našich analýz, některé rozdíly byly nevyhnutelné, tj. původní publikace dobytka údajů se odhaduje r2 s odlišným přístupem prováděnému v SNeP. Analýzy s SNeP byly na základě genotypů, zatímco původní analýza byla založena na dovodit dva locus haplotypy, které výsledky v publikovaných dat ukazuje očekávaný r2 0,32 na minimální vzdálenost, zatímco naše odhady byl 0.23. Podobně, Mbole-Kariuki et al. (2014) získal úroveň pozadí r2 = 0.013 kolem 2 Mb, zatímco náš odhad ve stejné vzdálenosti byl 0.0035 (údaje nejsou zobrazeny). Tudíž, protože naše odhady LD byly trvale menší než Mbole-Kariuki et al. (2014) očekává se, že naše odhady Ne by měly být větší. Zatímco toto zjištění zdůrazňuje význam pečlivého výběru parametrů a jejich limitů, je důležité zdůraznit, že i když absolutní velikost Ne hodnoty se liší, trendy jsou téměř totožné.
Švýcarský Ovce Příklad
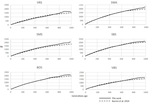
šest Švýcarských plemen ovcí analyzovány s SNeP vyrábí srovnatelné výsledky s těmi z původního papíru (Obrázek 2), s většinou překrývají Ne trend křivky (Obrázek 3). Obecný trend v Ne však ukázal pokles směrem k současnosti. SNeP produkoval mírně větší hodnoty Ne pro vzdálenější minulost (700-800 generací). To je způsobeno odlišným systémem binning používaným v SNeP, který umožňuje uživateli získat rovnoměrnější distribuci párových srovnání v každém zásobníku (tj., počet SNP párových srovnání v každém zásobníku je srovnatelný). Pro časové rozpětí přesahující 400 před generacemi, Burren et al. (2014) použili pouze tři přihrádky ve své analýze (střed na 400, 667 a 2000 generací), zatímco pro stejné časové rozpětí SNeP používá 5 přihrádek, s řadou párových porovnání závislé na rozsahu definovaných vzorců 6a,b. V důsledku toho, Burren a kolegů přístup končí s vyšší hustotou údaje popisující nejnovější generace, než popisuje nejstarší generace. Proto použití méně zásobníků má tendenci zvyšovat přítomnost menších hodnot Ne v každém zásobníku, čímž se snižuje průměrná hodnota Ne pro každý zásobník. Hodnoty Ne pro nedávnou minulost, ve srovnání s 29. generací v minulosti, přinesly velmi podobné výsledky. Největší rozdíl (50) byl získán pro plemeno SBS.

Obrázek 2. Srovnání mezi nedávnými hodnotami Ne vypočtenými na 29. generaci v této práci a Burren et al. (2014) pro šest švýcarských plemen ovcí.
Obrázek 3. Srovnání trendů Ne za posledních 250 generací v datech SHZ získaných Mbole-Kariuki et al. (2014) (přerušovaná čára) a pomocí SNeP (plná čára).
Diskuse
Analýza Ne pomocí LD data byla poprvé prokázána před 40 lety, a byl uplatňován, rozvíjen a zdokonalován od (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin a kol., 2012; Sved a kol., 2013). Tradičně malý počet analyzovaných SNP již není omezením, protože SNP čipy obsahují extrémně velký počet SNP, dostupných v krátkém čase a za rozumnou cenu. To podpořilo použití metody, která byla aplikována na člověka (Tenesa et al ., 2007; McEvoy et al., 2011) a také několika domestikovaným druhům (Anglie et al., 2006; Uimari a Tapio, 2011; Corbin a kol., 2012; Kijas a kol., 2012). Spolu s těmito vylepšeními, metodická omezení se projevila a byla zde řešena, přičemž většina úsilí směřovala ke správnému odhadu nedávné Ne. Kvantitativní hodnota odhadu je však velmi závislá na velikosti vzorku, typu odhadu LD a procesu binningu (Waples and Do, 2008; Corbin et al., 2012), zatímco jeho kvalitativní vzorec závisí více na genetické informaci než na manipulaci s daty.
Tak daleko, tato metoda byla aplikována pomocí různých software, žádný standardizovaný přístup existuje bin výsledky a každý obor se uplatňuje více či méně arbitrární přístup, např. binning pro generaci třídy v minulosti (Corbin et al., 2012), binning for distance classes with a constant range for each bin (Kijas et al., 2012) nebo binning per distance classes lineárním způsobem, ale s většími zásobníky pro novější časové body (Burren et al ., 2014). Podle našich znalostí je jediným dostupným softwarem, který odhaduje Ne prostřednictvím LD, NeEstimator (Do et al., 2014), upgradovaná verze bývalého LDNE (Waples and Do, 2008) umožňující analýzu velkého datového souboru (as 50k SNPChip). Důležité je, že zatímco SNeP se zaměřuje na odhad historického Ne trendy, NeEstimator cílem je vyrábět moderní nestranné Ne odhady, mělo by proto být považováno za doplňující nástroj při zkoumání demografie prostřednictvím LD.
Použili jsme SNeP k analýze dvou datových souborů, kde byla metoda dříve použita. Výsledky, které jsme získali pro data ovcí, byly kvantitativně i kvalitativně srovnatelné s výsledky získanými Burrenem et al. (2014), zatímco pro data Zebu jsme získali odhad trendu Ne, který se shodoval s odhadem Mbole-Kariuki et al. (2014) ačkoli naše bodové odhady Ne byly větší než odhady popsané pro data (Mbole-Kariuki et al., 2014). Rozdíl mezi těmito dvěma výsledky odráží to, že Burren a kolegy produkoval jejich r2 odhady pomocí PLINK (standardní software pro rozsáhlé SNP manipulaci s daty), který používá stejný přístup používá k odhadu r2 SNeP, zatímco Mbole-Kariuki a kol. následoval Hao et al. (2007) pro odhad r2. Použití různých odhadů pro LD je rozhodující pro kvantitativní aspekt zásady Ne křivka, kde vzhledem k hyperbolické korelace mezi Ne a r2, pokles v r2 na jeho rozsah blíže k 0 může vést k velké změně v Ne odhady, zatímco rozdíly v odhadech jsou méně významné, když r2 hodnota je vysoká, tj. blíže k 1. Proto, i když v jednom z datových souborů hodnoty Ne, kde se podstatně liší, v obou případech se křivky Ne překrývaly s původně publikovanými.
jak již bylo navrženo jinými autory, spolehlivost kvantitativních odhadů získaných touto metodou musí být brána s opatrností, zejména u hodnot Ne souvisejících s nejnovější a nejstarší generací (Corbin et al ., 2012), protože za posledních generací, velké hodnoty c jsou zapojeny, není vhodné teoretické důsledky, které Hayes navrhované odhadnout proměnnou, Ne v průběhu času (Hayes et al., 2003). Odhady pro nejstarší generace by mohla také být nespolehlivé, jako splývající teorie ukazuje, že ne SNP mohou být spolehlivě vzorku po 4Ne generací do minulosti (Corbin et al., 2012). Dále, ne odhady, a zejména ty, které souvisejí s generacemi dále v minulosti, jsou silně ovlivněny faktory manipulace s daty, jako je volba hodnot MAF a alfa. Použitá strategie binningu může navíc narušovat obecnou přesnost metody, například tam, kde se k naplnění každého koše používá nedostatečný počet párových srovnání.
jednou z aplikací metody je porovnání demografie plemene. V tomto případě je tvar Ne křivky by bylo optimální nástroj, jak odlišit různé demografické historie, více než jejich číselné hodnoty, pomocí nich jako potenciální demografické otisků prstů pro dané plemeno, nebo druhy, ale brát v úvahu, že mutace, migrace, a výběr může ovlivnit Ne odhad přes LD (Waples a Dělat, 2010). Navíc, pečlivém zvážení data analyzována s SNeP (a další software pro odhad Ne), je velmi důležité, protože přítomnost matoucích faktorů, jako jsou příměsi, může mít za následek zkreslené odhady Ne (Orozco-terWengel a jedná se celkově o, 2014).
cílem SNeP je proto poskytnout rychlý a spolehlivý nástroj použít LD metody pro odhad Ne pomocí vysoké propustnosti genotypových dat ve více konzistentním způsobem. Umožňuje dva různé přístupy odhadu r2 plus možnost použití odhadů r2 z externího softwaru. Použití SNeP nepřekonává limity metody a teorie za ní, přesto umožňuje uživateli aplikovat teorii pomocí všech dosud navržených oprav.
autorské příspěvky
MB vytvořil a napsal software a rukopis. MB, MT a POtW testovali software a provedli analýzy. MT, POtW, a MWB revidoval rukopis. Všichni autoři schválili konečný rukopis.
Prohlášení o střetu zájmů
autoři prohlašují, že výzkum byl proveden bez jakýchkoli obchodních nebo finančních vztahů, které by mohly být vykládány jako potenciální střet zájmů.
poděkování
Děkujeme Christine Flury za poskytnutí údajů o ovcích a za užitečnou diskusi. Děkujeme také dvěma recenzentům za užitečné návrhy na zlepšení tohoto příspěvku. MB byl podporován programem Master a zpět (Regione Sardegna).
Olivy, B., Nordborg, M., a Olivy, D. (1997). Účinky lokálního výběru, vyváženého polymorfismu a výběru pozadí na rovnovážné vzorce genetické rozmanitosti v rozdělených populacích. Genete. Rez.70, 155-174. doi: 10.1017/S0016672397002954
PubMed Abstrakt | Plný Text | CrossRef Plný Text | Google Scholar
Vrána, J. F., a Kimura, M. (1970). Úvod do teorie populační genetiky. New York, NY: Harper a Row.
Google Scholar
Ohta, T., and Kimura, m. (1971). Vazebné nerovnováhy mezi dvěma oddělování nukleotidů stránky pod stálým tokem mutací v konečné populaci. Genetika 68, 571-580.
PubMed Abstract / Full Text / Google Scholar
Wright, s. (1943). Izolace podle vzdálenosti. Genetika 28, 114-138.
PubMed Abstrakt / Plný Text / Google Scholar