Prealgebra
Výsledky Učení
- Najít oblast, základny a výšky trojúhelníku,
- Najděte délka jedné strany trojúhelníka daného obvodu a dvě jiné délky
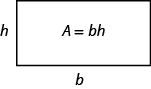
nyní víme, jak najít oblast obdélníku. Tuto skutečnost můžeme použít k vizualizaci vzorce pro oblast trojúhelníku. V obdélníku níže jsme označili délku b a šířku h, takže plocha je bh.
plocha obdélníku je základna, b, krát výška, h.
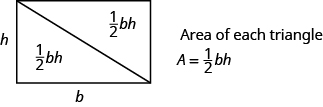
tento obdélník můžeme rozdělit na dva shodné trojúhelníky (viz obrázek níže). Trojúhelníky, které jsou shodné, mají stejné délky a úhly stran, takže jejich plochy jsou stejné. Plocha každého trojúhelníku je polovina plochy obdélníku nebo \frac{1}{2}bh. Tento příklad nám pomáhá zjistit, proč je vzorec pro oblast trojúhelníku a= \ frac{1}{2}bh.
obdélník lze rozdělit na dva trojúhelníky stejné plochy. Plocha každého trojúhelníku je polovina plochy obdélníku.
vzorec pro oblast trojúhelníku je a= \ frac{1}{2}bh, kde b je základna a h je výška.
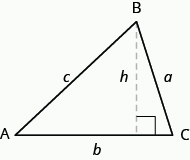
Chcete-li najít oblast trojúhelníku, musíte znát jeho základnu a výšku. Základna je délka jedné strany trojúhelníku, obvykle strany dole. Výška je délka čáry, která spojuje základnu s protilehlým vrcholem a vytváří \text{90}^ \Kruhový úhel se základnou. Obrázek níže ukazuje tři trojúhelníky se základnou a výškou každého označeného.
výška h trojúhelníku je délka úsečky, která spojuje základnu k protější vrchol a dělá \text{90}^ \circ úhel se základnou.

vlastnosti trojúhelníku
pro libovolný trojúhelník \Delta ABC je součet měr úhlů \text{180}^ \circ.
m \ úhel{a}+m \ úhel{B}+M \ úhel{C}=180^\circ
obvod trojúhelníku je součtem délek stran.
P=a+b+c
obsah trojúhelníku je polovina základny, b, krát výška, h.
A=\frac{1}{2}bh
příklad
najděte oblast trojúhelníku, jehož základna je 11 palců a jehož výška je 8 palců.
řešení
| Krok 1. Přečtěte si problém. Nakreslete obrázek a označte jej danými informacemi. |  |
| Krok 2. Určete, co hledáte. | plocha trojúhelníku |
| Krok 3. Název. Vyberte proměnnou, která ji bude reprezentovat. | nechť a = plocha trojúhelníku |
| Krok 4.Přeložit.
napište příslušný vzorec. nahradit. |

|
| Krok 5. Vyřešte rovnici. | a=44 čtverečních palců. |
| Krok 6. Kontrola:
A=\frac{1}{2}bh 44 \ stackrel{?}{=}\frac{1}{2}(11)8 44=44\zaškrtnutí |
|
| Krok 7. Odpověz na otázku. | plocha je 44 čtverečních palců. |
příklad:
obvod trojúhelníkového zahrada je 24 metrů. Délky dvou stran jsou 4 nohy a 9 chodidla. Jak dlouho je třetí strana?
příklad:
oblast trojúhelníkového tvaru kostelního okna je 90 metrů čtverečních. Základna okna je 15 metrů. Jaká je výška okna?
Rovnoramenného a Rovnostranných Trojúhelníků
Kromě pravoúhlého trojúhelníku, některé jiné trojúhelníky, které mají zvláštní jména. Trojúhelník se dvěma stranami stejné délky se nazývá rovnoramenný trojúhelník. Trojúhelník, který má tři strany stejné délky, se nazývá rovnostranný trojúhelník. Obrázek níže ukazuje oba typy trojúhelníků.
v rovnoramenném trojúhelníku mají dvě strany stejnou délku a třetí strana je základna. V rovnostranném trojúhelníku mají všechny tři strany stejnou délku.
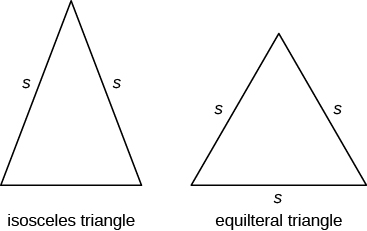
rovnoramenné a rovnostranné trojúhelníky
rovnoramenný trojúhelník má dvě strany stejné délky.
rovnostranný trojúhelník má tři strany stejné délky.
příklad
obvod rovnostranného trojúhelníku je 93 palců. Najděte délku každé strany.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. Šátek bude rovnoramenný trojúhelník se základnou
60 palců. Jak dlouho může dělat dvě stejné strany?








