Dne 31. Května 1832, francouzské Republikánské revoluční nazývá Évariste Osnova zemřela na střelnou. Bylo mu 20 let. Noc předtím, ze strachu z vlastní smrti, Galois napsal mnoho dopisů, freneticky čmáral „nemám čas; nemám čas“. Jedno písmeno je zvláště cenné z historických důvodů. V tomto dopise Galois tvrdí, že revoluci skutečně spustil. Ne politickou. Ale matematický.

revoluce Osnova zahájeno ukázalo být větší a hlubší, než on mohl možná si to představuji! Krajina matematiky byla hluboce ovlivněna galoisovou vizí, jak její potomci povstali a převzali matematický svět. Toto potomstvo je nyní všudypřítomné a vládne neomezeným zemím. Jde pod názvem čistá algebra.

idealizovat i trochu více na příběh, vyprávění, Osnova‘ dramatický život, tady je abstrakt dokument o algebře.

rozhodně je! Jeho matematická revoluce ale neprošla hladce. Jako každý vůdce revoluce měl nejprve největší potíže. Nechci si představit revoluci. Ale přesvědčit ostatní, aby se k němu připojili ve hře měnícím se přístupu k matematice. Když Osnova byla ještě naživu, jeho revoluční myšlenky odmítli několikrát do francouzské akademie vědy… Protože nejlepší francouzsky matematici té doby, jako Siméon Denis Poisson prostě nemohl dostat to! Částečně kvůli Galoisovu nečitelnému rukopisu zobrazenému vpravo …

V roce 1843, 10 let poté, Osnova‘ smrti, nakonec, geniální francouzský matematik Joseph Liouville podařilo pochopit některé z Osnova‘ nápady. Po dalších 3 letech práce publikoval Liouville článek, který je vysvětlil. Ale Liouvilleův článek byl stále příliš přitažený za vlasy, aby si ostatní matematici mohli užívat a rozumět jim. Trvalo dalších 24 let najít francouzský matematik dost vynikající pro lepší pochopení Osnova a aby jeho myšlenky, průzračné. Tento vynikající matematik je Camille Jordan. Ve skutečnosti, Jordan 1870 kniha o Osnova teorie byla tak dobře napsaná, že německý matematik Felix Klein zjistil, že je čitelný jako německá kniha!

byla to určitě Obrovská vzpruha. Trvalo by však dalších 82 let, než by velký rakouský matematik Emil Artin konečně dal Galoisově teorii moderní podobu v roce 1942. Artin si zaslouží hodně kreditů. Zatímco Galois byl vizionář, který předvídal tuto revoluci, Artin, v mnoha smyslech, je ten, kdo skutečně podnikl revoluci a převrátil matematiku. Díky Artin, a pár dalších, dnes, Osnova teorie se stala nevyhnutelnou kamenem výzkumu v matematice, s dostatkem překvapující a úžasné úspěchy (jako Wiles‘ důkaz velká Fermatova věta), stejně jako obrovský rezervoár otevřených otázek a záhad!

pole v čisté algebře

Galoisova teorie je o symetrii čísel. Ale než se tam dostanu, musím vás představit, abych vás vyzbrojil tím, že vám řeknu tajemství o číslech. A jsem si jistý, že jste o tom slyšeli! Opravdu, na střední škole, pravděpodobně jste se učili nikdy neopouštět kořeny ve jmenovatelích.

myslím, že $1 / (\sqrt{2}-1)$ nebyla správná odpověď. Můžete pomoci zbavit se druhé odmocniny 2 ve jmenovateli?

Hehe … naučili jsme se násobit nahoru a dolů konjugátem jmenovatele. Tento konjugát se získá nahrazením $ – $ $ + $ (nebo naopak) ve jmenovateli.

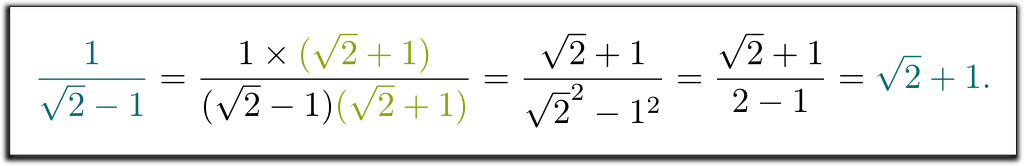
já vím! Komplikovaný výraz $1 / (\sqrt{2}-1)$ představuje stejné číslo jako $ \ sqrt{2}+1$. A to vysvětluje, proč naši učitelé chtěli, abychom psali výsledky spíše jedním způsobem než druhým: když je vše napsáno stejným způsobem, zkoušky se mnohem snadněji opraví!

ale co $ 1 / (\sqrt{2}-1)$? Můžete se zbavit kořene ve jmenovateli? Dá se to vůbec udělat?

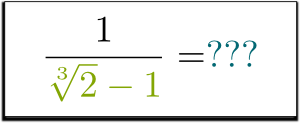
já vím!

Řekni mi to!

nějaké štěstí?

hehe … je zajímavé, že jakákoliv mocnina $ \ sqrt{2}-1$ může být zapsána jako součet mocnin $ \ sqrt{2}$. Opravdu, stačí, aby distribuovat tyto produkty:

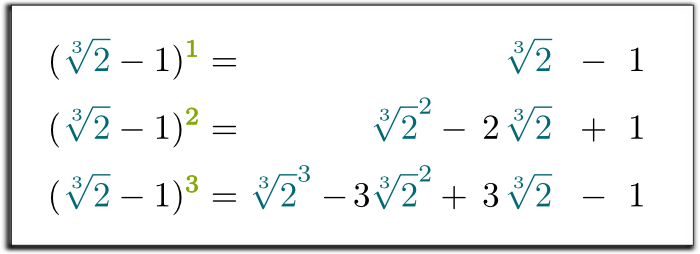
Ano je! Provedením této substituce ve třetí rovnici jsme ukázali, že tři první mocniny $ \ sqrt{2}-1$ lze zapsat jako součet racionálního čísla $\sqrt{2}$ a $ \ sqrt{2}^2$!

takže nyní máme 3 rovnice, se 2 kořenovými výrazy se chceme zbavit! Můžeme tedy kombinovat rovnice a odstranit všechny kořenové výrazy vpravo!

Pojďme vynásobit 2 první řádky o 3 a sečíst všechny 3 rovnice:

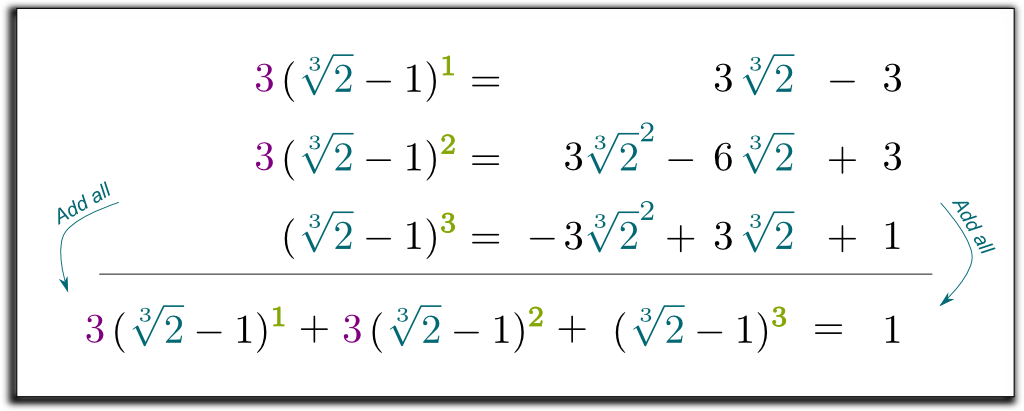
Hehe … skvělá věc je, že levý výraz, který jsme získali, lze nyní faktorizovat pomocí $ \ sqrt{2}-1$! Dovolte mi přeskočit některé nudné výpočty … a dostat se k výsledku $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Abychom se zbavili kořenů ve jmenovateli, můžeme vynásobit nahoru a dolů $ \ sqrt{2}^2 + \ sqrt{2} + 1$! Nakonec získáme následující překvapivý a krásný vzorec:

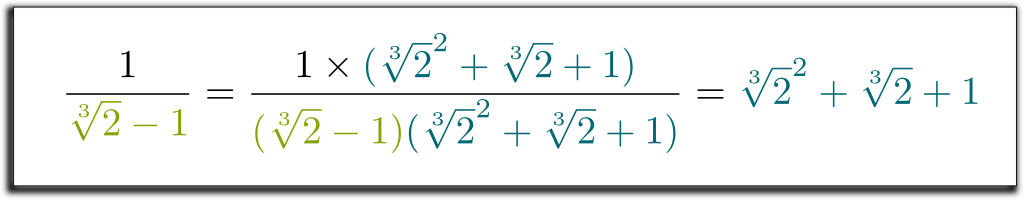
já vím! Ale ještě hezčí je, že metoda, kterou jsme použili, je velmi obecná! S podobnou technikou můžeme nyní odstranit všechny radikály z jmenovatelů!

to, co bylo pro Galoise obzvláště zajímavé, nebyla skutečnost, že metoda umožnila odstranit radikály z jmenovatelů. Ale spíše, že jakékoli číslo s radikály ve jmenovatelích se rovnalo číslu s radikály nahoře. To znamenalo, že čísla s radikály nahoře byla podle rozdělení stabilní.

je běžné označovat $ \ mathbb Q{2}]$ množinu čísel, která lze zapsat jako součet mocnin $ \ sqrt{2}$. Vzhledem k tomu, $ \ sqrt{2}^3 = 2$ je racionální číslo, jakýkoliv součet mocnin $ \ sqrt{2}$ může být ve skutečnosti zapsán ve standardním formuláři $a\sqrt{2}^2 + b \ sqrt{2} + C$. Nyní, pokud přidáte, odečtete nebo vynásobíte jakákoli dvě taková čísla, pak není těžké vidět, že získáme čísla, která lze stále vložit do standardního formuláře $a\sqrt{2}^2 + b \ sqrt{2} + C$. Navíc jsme zde právě ukázali, že inverzní hodnota všech čísel $a\sqrt{2}^2 + b \ sqrt{2} + C$ může být také zapsána ve standardním formuláři. To ukazuje, že žádné sčítání, odčítání, násobení a dělení čísel v $\mathbb Q{2}]$ dává číslo, které lze zapsat ve standardní formě a patří tedy do $\mathbb Q{2}]$. Z čistě algebry, $ \ mathbb Q{2}]$ je tedy stabilní čtyřmi klasickými aritmetickými operacemi. Z tohoto důvodu tomu říkáme pole.

Geometrie Oblasti Rozšíření

pole, které jsou nejvíce obeznámeni s je pravděpodobně nastavit $\mathbb Q$ racionálních čísel. Dalšími příklady polí jsou množiny $\mathbb R$ reálných čísel a množina $ \ mathbb C$ komplexních čísel. A teď máme také $ \ mathbb Q{2}]$. Protože $ \ mathbb Q{2}]$ je pole, které obsahuje pole $ \ mathbb Q$, říkáme, že $ \ mathbb Q{2}] / \ mathbb Q$ je rozšíření pole.

skutečnost, že $ \ mathbb Q{2}] / \mathbb Q$ je rozšíření pole, poskytuje velmi přirozené spojení mezi oběma poli. Konkrétně $ \ mathbb Q{2}]$ lze považovat za vektorový prostor, kde $ \ mathbb Q$ je skalární pole. Zejména skutečnost, že jakékoli číslo v $\mathbb Q{2}]$ lze psát $\sqrt{2}^2 + b\sqrt{2} + c$ znamená, že $(1, \sqrt{2}, \sqrt{2}^2)$ tvoří základ $\mathbb Q{2}]$ jako $\mathbb Q$-vektorový prostor. A to znamená, že jej můžeme geometricky reprezentovat jako 3-rozměrný prostor!

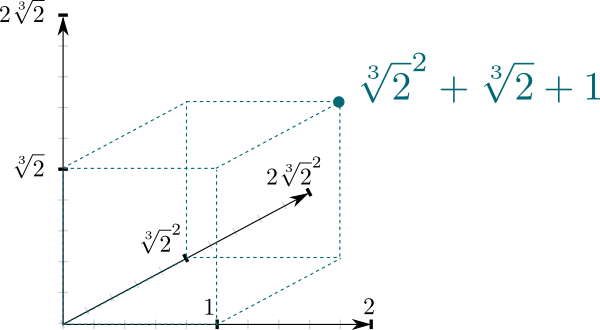
rozměr vektorového prostoru výše je zajímavou vlastností rozšíření polí. Je známý jako stupeň a běžně se označuje $ \ big{2}]: \ mathbb Q\big] = 3$ například.

Ano! Je to vlastně docela snadné vytvořit rozšíření pole tohoto: stačí přidat nějaké radikální číslo, které nepatří do $ \ mathbb Q{2}]$!

Ano! Tím by se vytvořilo pole $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$. Tato pole obsahují všechna čísla, která jsou produkty a součty $\sqrt{2}$ a $\sqrt{2}$. Jsou ve tvaru $a \ sqrt{2}^2 $ +$b \ sqrt{2}+c$+$ d \ sqrt{2}^2 \ sqrt{2}$ +$ e \ sqrt{2} \sqrt{2} $ + $ f \ sqrt{2}$. Máte představu o tom, jaký je titul $ \ big{2}, \ sqrt{2}]: \ mathbb Q{2}]\big]$?

Ano! Vskutku, máme $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e \sqrt{2} + f) \sqrt{2}$. Tedy, každé číslo $\mathbb Q{2},\sqrt{2}]$ lze psát $A+B\sqrt{2}$, kde $A$ a $B$ patří do $\mathbb Q{2}]$. Takže 2 skaláry $ \ mathbb Q{2}] $ určují číslo v $ \ mathbb Q{2}, \ sqrt{2}]$. To znamená, že stupeň rozšíření pole $ \ mathbb Q{2}, \sqrt{2}] / \ mathbb Q{2}]$ je 2. Ve skutečnosti máme vztah Chasles $ \ big{2}, \ sqrt{2}]: \ mathbb Q \big] $ = $ \ big{2}, \sqrt{2}] : \mathbb Q{2}] \big] \ big{2}]: \ mathbb Q \ big] $ = $ 2 \ krát 3 = 6$.

je to lepší než to! Každé rozšíření pole konečného stupně, nazývané konečné rozšíření pole, je překlenuto jedním číslem. Například $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, což znamená, že všechny čísla, která jsou sumy síly $\sqrt{2}$ a $\sqrt{2}$ jsou také sumy síly $\sqrt{2} + \sqrt{2}$. Není to překvapivě úžasné?

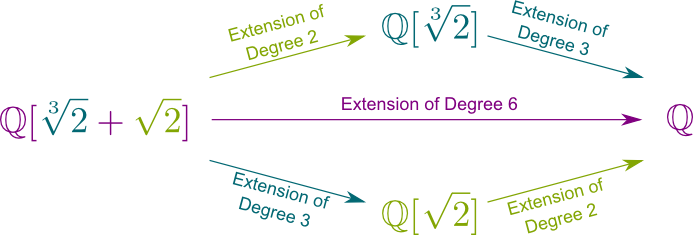
Více obecně, nějaké omezené oblasti rozšíření $\mathbb Q$ lze psát $\mathbb Q$ s $x$, která je přidán do $\mathbb Q$.

Ano. Je to případ rozšíření pole $ \ mathbb R / \ mathbb Q$. A stejně tak je nejdůležitější rozšíření pole v galoisově teorii! Toto rozšíření pole je $ \ bar {\mathbb Q} / \mathbb Q$, kde $ \ bar {\mathbb q}$ je množina algebraických čísel. Toto jsou všechna řešení polynomiálních rovnic tvaru $a_n x^n $+$ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $+$ a_0 = 0$. Například $ \ sqrt{2}$ je algebraické číslo, protože je řešením $x^4-2x = 0$. Proto $ \ bar {\mathbb Q}$ je rozšíření pole pro všechna konečná rozšíření pole $ \ mathbb Q$.

konjugovaná čísla

jsme skoro tam! Potřebujeme Poslední objížďku přes polynomiální rovnice.

přesně tak! Galois si všiml, že některé rovnice lze zjednodušit. Například $x^4-2x=0$ lze faktorizovat jako $x (x^3-2)=0$, což odpovídá $x=0$ nebo $x^3-2=0$. Takže rovnice $x^4-2x=0$ může být redukována na rovnice $x=0$ a $x^3-2=0$. A ve skutečnosti je toto snížení velmi podobné tomu, jak lze čísla jako 35 snížit na 5 a 7, protože $5 \krát 7 = 35$. Podobnost mezi rovnicemi a celými čísly je tak silná, že můžeme dokonce vytvořit euklidovské dělení polynomů, stejně jako jste se to naučili pro čísla! Vpravo je příklad takového rozdělení (nebojte se, pokud tomu nerozumíte,nebude to důležité pro pokračování).

přesně! Ty jsou známé jako neredukovatelné polynomiální rovnice. Rovnice $x^3-2=0$ je příkladem neredukovatelné polynomiální rovnice.

Ano! Ale hlavně se Galois chtěl zaměřit na rovnice s racionálními koeficienty. Nebo spíše polynomy s koeficienty, které patří do základního pole. Takže to, co jsem měl na mysli, bylo, že pro $\mathbb Q$ jako základní pole, $x^3-2=0$ je neredukovatelný.

uvažujme $x^2-2x -1=0$, abychom měli nějaké stopy. Tato rovnice může být prokázána jako neredukovatelná. Pamatujete si, jak to vyřešit?

Pokud $b^2-4ac \ geq 0$, Ano.

přesně tak! Takže neredukovatelná polynomiální rovnice $x^2 + 2x -1=0$ má dvě řešení: $1+ \ sqrt{2}$ a $ 1 – \sqrt{2}$ … jakýkoli komentář?

Bingo! To je klíčový objev Galoise. Obecněji, Galois volal konjuguje všechna řešení neredukovatelné polynomiální rovnice. A jak si dokážete představit, jsou nezbytné pro odstranění radikálů z jmenovatelů!

první věc, kterou všimnete, je, že je-li $x_1$, $x_2$, …, $x_n$ jsou všechna řešení polynomu irreducible rovnice $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ s racionálními koeficienty, pak se tento polynom ireducibilní rovnice může být ve skutečnosti přepsána $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Identifikace konstantních podmínek pak přináší $x_1 x_2 … x_n $ = $ (-1)^n a_0 / a_n$. Součinem konjugovaných čísel je tedy racionální číslo $(-1)^n a_0/a_n$, které je nenulové (dokažte to!).

Tady je jen vtip, jak udržet v mysli silné spojení mezi konjugáty:

zvažte zlomek $1 / x_1$, kde $x_1$ je komplikovaný výraz s radikály. Vynásobením nahoru a dolů konjugáty $x_2$, …, $x_n$ z $x_1$, pak výnosy $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, který nemá žádné radikální ve jmenovateli, jako jsme navázali $a_0$ být nenulové číslo základního pole!

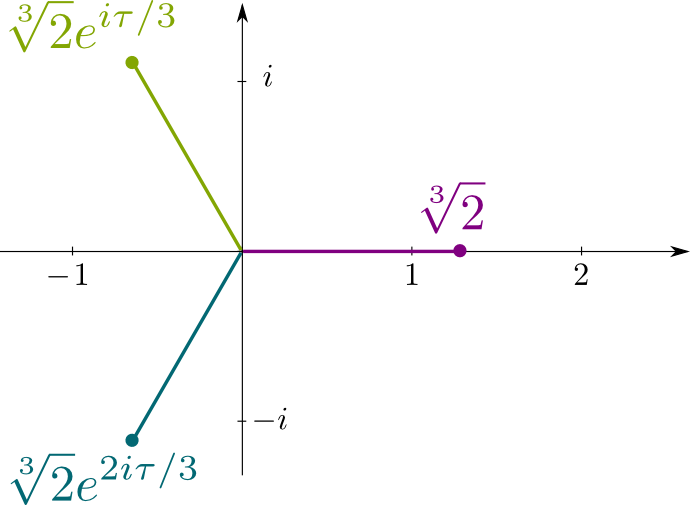
připomeňme, že $x^3-2=0$ je neredukovatelná polynomiální rovnice $\sqrt{2}$ je řešení. Takže, konjugáty jsou další řešení této rovnice, které jsou komplexní čísla $\sqrt{2}j$ a $\sqrt{2}j^2$, kde $j= e^{i\tau/3}$ $\tau = 2\pi$ je poměr obvodu kruhu a jeho poloměru. Následující obrázek zobrazuje umístění konjugát řešení v této komplexní rovině,

Osnova‘ Nejednoznačnost

Konečně se dostáváme k Osnova je klíčový vhled!

konjugáty jsou dokonale permutovatelné. To znamená, že pokud systematicky měníte $ \ sqrt{2}$ svým konjugátem $ – \sqrt{2}$, pak stále platí rovnosti. Například, protože jsme měli $1 / (\sqrt{2}-1) = \sqrt{2}+1$, Mohu vám přímo říci, že $1 / (- \sqrt{2}-1)= – \sqrt{2}+1$! Podobně máme následující ohromující důsledky:

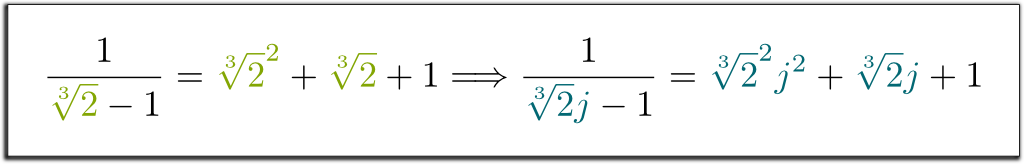
Hehe … dovolte mi nejprve připomenout, že konečná pole jsou překlenuta jediným prvkem. Pokud je tedy základní pole $ \ mathbb Q$, může být jakékoli konečné pole zapsáno $ \ mathbb Q$ pro některé správné $x_1$. Nyní zvažte $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ neredukovatelná polynomiální rovnice $x_1$ je řešením. Poté, co definuje $\mathbb Q$ je $\mathbb Q$-vektorový prostor překlenul tím, že $x_1$, $x_1^2$, …, $x_1^{n-1}$, se zjednodušením větší pravomoci $x_1$, tedy algebraické pravidlo $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

přesně tak! Rozhodující je, že tato algebraická pravidla $\mathbb Q$ opravdu nezávisí na povaze $x_1$; závisí pouze na neredukovatelném polynomu $x_1$ je řešením! Proto jsou pravidla $\mathbb Q$ identická s pravidly $ \ mathbb Q$,…, $\mathbb Q$, kde $x_1$ je nahrazen jedním z jeho konjugátů $x_2$,…, $x_n$. Zejména pole $ \ mathbb Q{2}]$ a $ \ mathbb Q{2} j]$ fungují podle přesně stejných pravidel. Proto jsou konjugáty dokonale proměnlivé! Můžeme říci, že pole $\mathbb Q{2}]$ a $\mathbb Q{2} j]$ jsou isomorfní, a to nahrazením $\sqrt{2}$ $\sqrt{2}j$ je izomorfismus $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

velmi podobným (ale silnějším) způsobem, že dva vektorové prostory Dimenze 2 jsou víceméně stejné! To má hrozný důsledek. To znamená, že z algebraického hlediska je nesmyslné, aby se rozdíl mezi číslem a některý z jeho konjugáty (tak dlouho, jak budete systematicky nahradit číslo jeho konjugát)! Takže například $ \ sqrt{2}$ a $ – \sqrt{2}$ jsou algebraicky nerozeznatelné! Abych to měl na paměti, tady je další vtip, se kterým jsem přišel:

vůbec ne! Rozdíl mezi těmito dvěma čísly musí zahrnovat matematiku, než některé jiné algebry, jako aby vztahy nebo topologie. Co chci říct je, že, například, vztahu $\sqrt{2} > 0$ dělá rozdíl mezi $\sqrt{2}$ $- \sqrt{2}$, ale to je proto, že zahrnuje objednávku vztahu. Ale pokud se omezíme na polynomiální rovnosti, pak není absolutně žádný rozdíl mezi $ \ sqrt{2}$ a $ – \sqrt{2}$. Podobně $i$ a $ – i$, řešení neredukovatelné polynomiální rovnice $x^2+1=0$, jsou také algebraicky nerozeznatelná. Přesto voláme libovolně $i$ jeden z nich. To je důvod, proč Galois nazval svou teorii teorií nejednoznačnosti. Dnes, nejednoznačnost výběru konvenční odmocnina ze $-1$ mezi $i$ a $-i$ je spíše nazývá symetrie mezi $i$ a $-i$.

Osnova Skupin

Osnova zaměřili zejména na oblasti rozšíření, které jsou stabilní, podle conjugacy. Taková stabilní rozšíření pole jsou nyní známá jako rozšíření Galois. Pokud tedy $x_1$ patří do rozšíření Galois, pak toto rozšíření Galois obsahuje všechny konjugáty $x_2$,…, $x_n$.

jednoduchý způsob, jak postavit Osnova rozšíření spočívá v tom, že pole zaklenuta řešení ireducibilní polynom rovnice. Například, je-li $x_1$, …, $x_n$ jsou konjugáty pro základní pole $\mathbb Q$, pak $\mathbb Q / \mathbb Q$ je Osnova souboru. Takto vytvořená pole se nazývají rozdělovací pole.

například, rozdělení pole z rovnice $x^3-2=0$ je Osnova rozšířením $\mathbb Q{2}, \sqrt{2} j \sqrt{2} j^2] / \mathbb Q$ překlenul tím, že jeho řešení.

Pokud $x_1$ překlenuje galoisovu příponu, pak i její konjugáty. Tak, $ \ mathbb Q = \ mathbb Q = $ … $= \ mathbb Q$ = $\mathbb Q$. Takže izomorfismus mezi $ \ mathbb Q$ A $\mathbb Q$, který spočívá v tom, že vždy nahradí $x_1$ $x_2$, je ve skutečnosti izomorfismus mezi $ \ mathbb Q$ A sám! Říkáme tomu automorfismus. Automorfizmy Osnova rozšířením $\mathbb Q/\mathbb Q$ forem Osnova skupiny $Gal(\mathbb Q/\mathbb Q)$.

Nyní, co je zásadní, pokud $\mathbb Q = \mathbb Q$, pak všechny automorfizmy Osnova rozšířením $\mathbb Q/ \mathbb Q$ jsou permutace $x_1$ s jedním z jeho konjugátů! Zejména zde vidíme, že kardinalita Galoisovy skupiny se rovná stupni Galoisova rozšíření.

jasně! Můžete si všimnout, že $\mathbb Q = \mathbb Q$ a $\mathbb Q = \mathbb Q$, což znamená, že $i$ a $\sqrt{2}$ každý překlenuje rozdělení polí ireducibilní polynom rovnice mají řešení. Takže $ \ mathbb Q / \mathbb Q$ A $ \ mathbb Q / \ mathbb Q$ jsou obě rozšíření Galois. Proto jejich automorfismy spočívají v nahrazení $i$ jedním z jeho konjugátů, $i$ nebo $ – i$ a nahrazení $ \ sqrt{2}$ $\sqrt{2}$ nebo $ – \sqrt{2}$. V prvních případech neměníme nic na čísla, což odpovídá nulové symetrii. Druhý případech mohou být zobrazeny jako axiální symetrií, jak je zobrazeno na obrázku níže:

Není to úžasné?

jasně! Pojďme do rozdělovacího pole $ \ mathbb Q{2}, \ sqrt{2}j, \sqrt{2}j^2]$ z $ x^3-2=0$. Ale než půjdeme dál, všimněme si, že $ \ mathbb q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.

vše, co musíme dokázat, je, že všechny generátory jednoho pole patří druhému. Začněme tím, že dokážeme, že generátory posledně jmenovaných, $\sqrt{2}$ a $j$, patří k prvním. Je to zřejmé pro $ \ sqrt{2}$. Nyní $j = (\sqrt{2} j) / \sqrt{2}$, tedy $j$ patří také do bývalého pole. To dokazuje, že všechny prvky $ \ mathbb Q{2}, j]$ patří do $ \ mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Recipročně je jednoduché, že všechny generátory bývalého pole, $\sqrt{2}$, $\sqrt{2}J$ a $\sqrt{2}j^2$, jsou produkty generátorů druhého pole. Obě pole jsou tedy stejná. A zejména $ \ mathbb Q{2}, j]/ \ mathbb Q$ je rozšíření Galois.

Hehe… pochopit symetrie $\mathbb Q{2}]$, budeme muset jít dál v Osnova‘ studie Osnova skupin…

Osnova Korespondence

problém s Osnova skupin je, že mohou být mimořádně velké a složité. To je zejména případ nekonečné skupiny $Gal (\bar{\mathbb Q}/\mathbb Q)$. Zatknout takové obrovské a složité skupiny, Galois měl skvělý nápad rozdělit je na menší kousky.

Úžasně, Osnova zjistil, že Osnova skupiny mohou být rozděleny do podskupin symetrie tím, že se díval jen na ty, které zanechat nějaký podpole beze změny. Například, $\mathbb Q$ je podpole $\mathbb Q{2},j]$, protože libovolný počet bývalých patří k druhé. Symetrie $ \ mathbb Q{2}, j]$, které nic nemění na $ \ mathbb Q$, tedy tvoří podskupinu Galoisovy skupiny $ \ mathbb Q{2}, j] / \mathbb Q$. Tyto symetrie tvoří galoisovu grupu $Gal (\mathbb Q{2}, j] / \mathbb Q)$.

já vím! Rád si představuji tyto symetrie jako způsoby, jak připojit $ \ mathbb q{2}, j]$ na $ \ mathbb Q$. Zde je zobrazen obrázek z „zapojení do“:

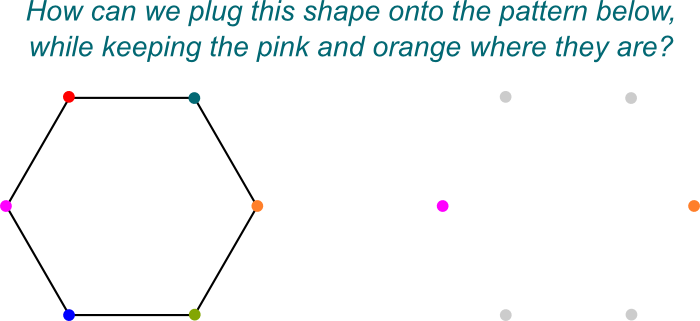
přesně tak! A to jednoduše proto, že $ \ mathbb Q{2}, j]$ je Galois rozšíření $ \ mathbb Q$, což je samo o sobě rozšíření pole $ \ mathbb Q$.

a je toho víc! Galois ukázal, že všechny podskupiny rozšíření Galois jsou získány tímto způsobem! Přesněji řečeno, mapování každém poli $K,$ v-mezi, Osnova rozšířením $\mathbb Q{2},j]$ a základní pole $\mathbb Q$ Osnova skupiny $Gal(\mathbb Q{2},j] / K)$ je bijektivní. Tato skutečnost se nazývá Galoisova korespondence! Tato korespondence je schematicky zobrazen níže pro rozšíření Galois $\mathbb Q/ \ mathbb Q$.

místo toho, abychom se pokusili popsat tuto skupinu přímo, Zaměřme se na její podskupinu $Gal(\mathbb Q{2}, j]/\mathbb Q)$. Je jednoduché, že $ \ sqrt{2}$ zahrnuje $ \ mathbb Q{2}, j]$ při přidání do $ \ mathbb Q$. Tak, $ \ mathbb Q{2}, j] / \ mathbb Q$ je Galois rozšíření překlenuté $ \ sqrt{2}$. Proto, s použitím věty jsme viděli dříve, víme, že všechny automorfizmy tato Osnova rozšíření spočívá v nahrazení $\sqrt{2}$ jedním z jeho 3 konjugáty (sám, $\sqrt{2} j$ a $\sqrt{2} j^2$)!

nyní bych mohl pokračovat ve studiu dalších kusů $Gal (\mathbb q{2}, j]/\mathbb Q)$, jako Galoisova podskupina $Gal (\mathbb Q{2},j]/ \ mathbb Q{2}])$. Ale raději použiji další z galoisových mocných vět. Konkrétně dokázal, že pokud $ \ mathbb Q/\mathbb Q$ bylo navíc samotné rozšíření Galois, pak podskupina $Gal(\mathbb Q{2}, j] / \mathbb Q)$ je normální.

to Znamená, že Osnova skupiny z $\mathbb Q{2},j]/\mathbb Q$ může být quotiented do této podskupiny, a podíl skupiny pak rovná $Gal(\mathbb Q/\mathbb Q)$. Přesto je $ \ mathbb Q / \mathbb Q$ skutečně galoisovým rozšířením o $j$, jehož konjugát je $j^2$. Tak, $Gal (\mathbb Q/ \ mathbb Q)$ spočívá buď v opuštění $j$ jako $j$ nebo jeho nahrazení $j^2$.

nyní můžeme odvodit všechny symetrie $Gal(\mathbb Q{2},j]/\mathbb Q)$ kombinací těchto $Gal(\mathbb Q{2},j] / \mathbb Q)$ a $Gal(\mathbb Q/\mathbb Q)$. Můžeme zobrazit tyto symetrie kreslení, jak ovlivňují naše tři spanning konjugáty $\sqrt{2}$, $\sqrt{2}j$ a $\sqrt{2}j^2$:

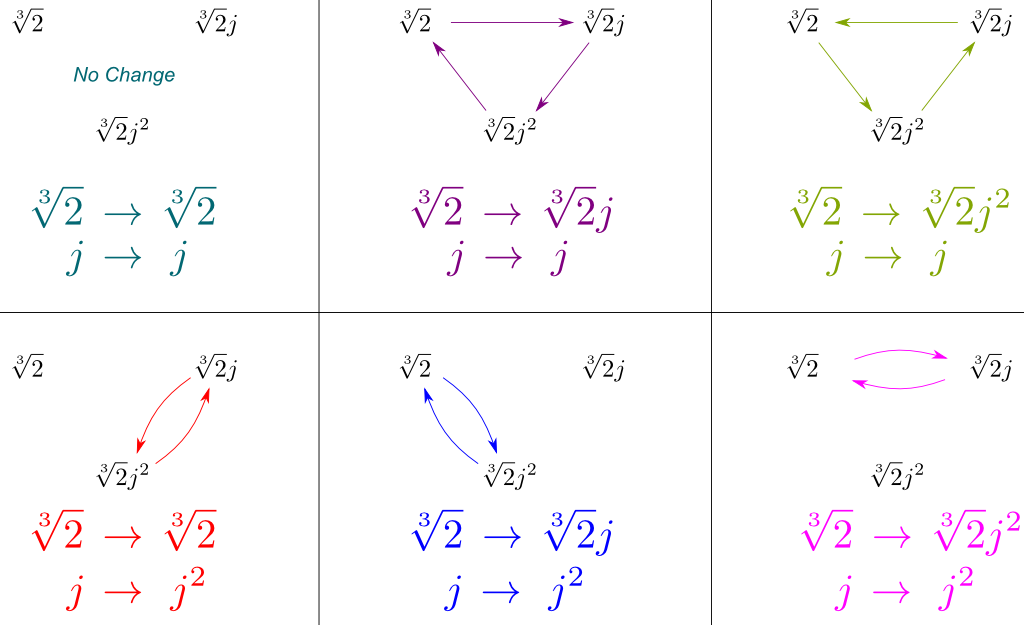
podstatné je, že výše uvedený obrázek obsahuje všechny symetrie $Gal (\mathbb Q{2},j]/\mathbb Q)$. A kupodivu tyto symetrie odpovídají známé skupině symetrie.

nechám Marcuse du Sautoye, aby vám to představil:

jsou zde symetrie jako hvězdice nebo jako trojúhelník?

ano, opravdu! Tato skupina symetrií trojúhelníku se nazývá $D_3$ a je stejná jako skupina $s_3$ permutací 3 prvků. To nás vede k následujícímu vzorci, který mi připadal tak krásný, že jsem se rozhodl to zarámovat!

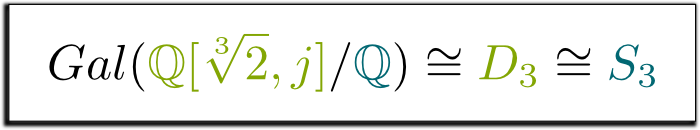
Pojďme Závěr

V mnoha ohledech, Osnova je považován za otce moderní algebry. Jeho klíčovou myšlenkou bylo podívat se na matematiku prostřednictvím úhlu pravidla operací, a to ho vedlo k odhalení překvapivé a podnětné nejasnosti, nebo symetrie, mezi čísly. Z algebraického hlediska jsou čísla jako $ \ sqrt{2}$, $ \ sqrt{2}J$ a $\sqrt{2}j^2$ skutečně dokonale symetrická a zcela zaměnitelná.

pochopení těchto symetrií mělo úžasné aplikace mimo jiné v algebraické geometrii a algebraické topologii. Zejména, rané úspěchy teorie zahrnují klasifikaci konstruovatelných pravidelných polygonů a větu, která tvrdí, že polynomiální rovnice vysokého stupně nelze vyřešit radikály.

Nedávné úspěchy objevit v kryptografii a Andrew Wiles‘ důkaz velká Fermatova věta. Tento důkaz zahrnuje studium skupiny Galois $Gal (\bar{\mathbb Q} /\mathbb Q)$ s reprezentací skupiny. Ale řekl bych, že teorie je nějak ještě mladá a zbývá toho hodně objevit. Koneckonců, je to jedna z nejaktivnějších oblastí výzkumu v dnešním čistě matematickém výzkumu.

To by nás mělo vést platit mnoho dalších pocty Osnova‘ neuvěřitelný génius… Nech mě patří jeden po SocraticaStudios.