kalmanovy filtry

algoritmus používaný ke sloučení dat se nazývá Kalmanův filtr.

Kalmanův filtr je jedním z nejpopulárnějších algoritmů ve fúzi dat. Vynalezl v roce 1960 Rudolph Kalman, nyní se používá v našich telefonech nebo satelitech pro navigaci a sledování. Nejslavnější použití filtru bylo během mise Apollo 11 poslat a přivést posádku zpět na měsíc.

kdy použít Kalmanův filtr ?

Kalmanův filtr lze použít pro fúzi dat k odhadu stavu dynamického systému (vyvíjejícího se s časem) v přítomnosti (filtrování), minulosti (vyhlazování) nebo budoucnosti (predikce). Senzory zabudované do autonomních vozidel vydávají opatření, která jsou někdy neúplná a hlučná. Nepřesnost senzorů (šum)je velmi důležitým problémem a může být řešena filtry Kalman.

Kalman filtr se používá pro odhad stavu systému, označené x. Tento vektor je složen z polohy p a rychlost v.

Na každý odhad, spojujeme míra nejistoty P.

provedením fúze senzory, jsme se vzít v úvahu různé údaje o stejném objektu. Radar může odhadnout, že chodec je 10 metrů daleko, zatímco Lidar odhaduje, že je 12 metrů. Použití filtrů Kalman vám umožní mít přesnou představu o tom, kolik metrů je skutečně chodec, a to odstraněním šumu obou senzorů.

Kalmanův filtr může generovat odhady stavu objektů kolem něj. Pro odhad potřebuje pouze aktuální pozorování a předchozí předpověď. Historie měření není nutná. Tento nástroj je proto lehký a časem se zlepšuje.

jak to vypadá

stav a nejistotu představují Gausové.

Gaussian je spojitá funkce, pod kterou oblast je 1. To nám umožňuje reprezentovat pravděpodobnosti. Jsme na pravděpodobnosti k normálnímu rozdělení. Uni-modalita Kalmanových filtrů znamená, že máme vždy jeden vrchol pro odhad stavu systému.

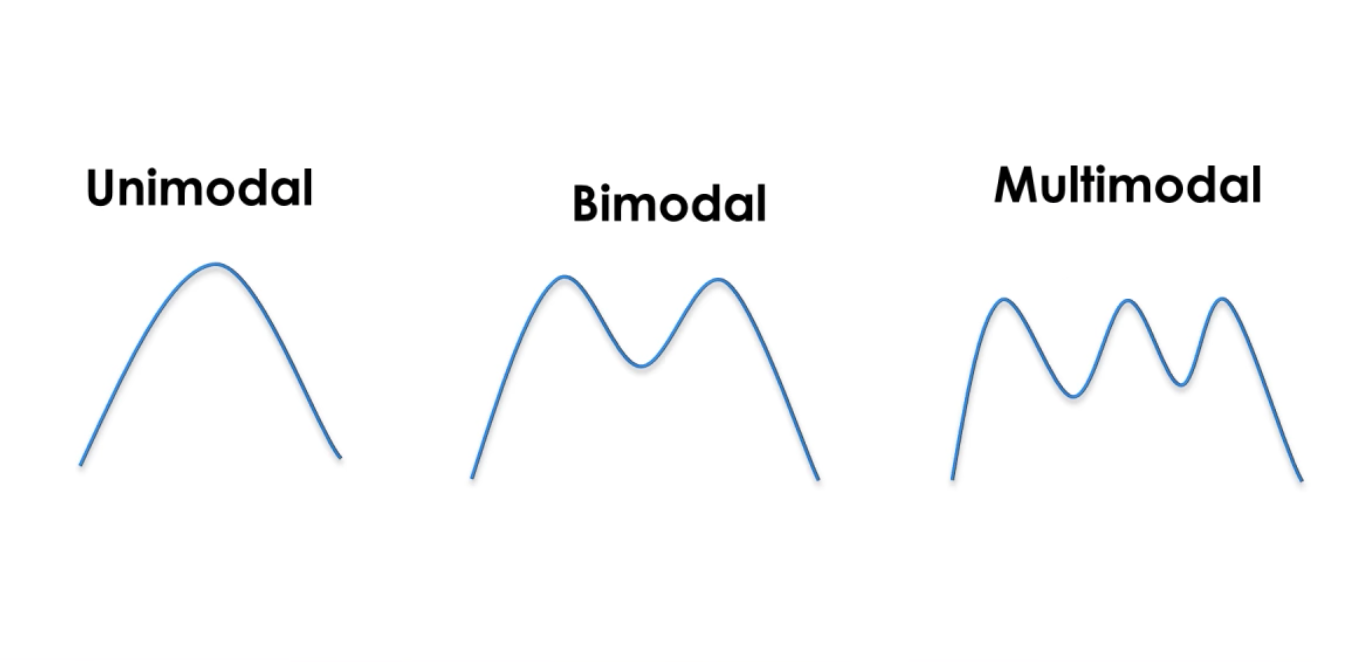
Máme na mysli μ představuje státem a rozptyl σ2 představuje nejistota. Čím větší je rozptyl, tím větší je nejistota.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Pozorování našich senzorů používáme k opravě předpokládaného stavu a získání přesnějšího odhadu.

odhadnout, Kalmanův filtr potřebuje pouze aktuální pozorování a předchozí predikce. Historie měření není nutná.

Matematika

Ta matematika za Kalman filtry jsou vyrobeny ze sčítání a násobení matic. Máme dvě fáze: predikce a aktualizace.

predikce
naše predikce spočívá v odhadu stavu x ‚a nejistoty P‘ v čase t z předchozích stavů x A P v čase t-1.

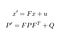
• F: Maticí přechodu od t-1 do t
• ν: Hluk přidáno
• Q: Kovarianční matice včetně hluku

Aktualizovat
aktualizace fáze se skládá z pomocí z měření ze senzoru na správné naše predikce, a tak předvídat, x a P.

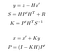
• y: Rozdíl mezi aktuální měření a predikce, tj. chyba.
• s: odhadovaná systémová chyba
• H: matice přechodu mezi markerem senzoru a naším.
• R: Kovarianční matice související s šumem senzoru (daná výrobcem senzoru).
• K: Kalman gain. Koeficient mezi 0 a 1 odráží potřebu opravit naši předpověď.

fáze aktualizace umožňuje odhadnout x a P blíže realitě, než jaké poskytují měření.

Kalmanův filtr umožňuje předpovědi v reálném čase, bez údajů předem. Používáme matematický model založený na násobení matic pro každou dobu definující stav x (pozice, rychlost) a nejistotu P.

Représentation Před/Zadní

Tento diagram ukazuje, co se stane v Kalmanův filtr.

• Předpokládané státní odhad představuje náš první odhad, naše předpověď fáze. Mluvíme o Prioru.
• měření je měření z jednoho z našich senzorů. Máme lepší nejistotu, ale hluk senzorů z něj činí měření, které je vždy obtížné odhadnout. Mluvíme o pravděpodobnosti.
• optimální odhad stavu je naše aktualizační fáze. Nejistota je tentokrát nejslabší, nashromáždili jsme informace a dovolili jsme generovat hodnotu jistější než pouze s naším senzorem. Tato hodnota je náš nejlepší odhad. Mluvíme o zadní straně.

to, co Kalmanův filtr implementuje, je vlastně Bayesovo pravidlo.

V Kalman filter, my smyčka předpovědi z měření. Naše předpovědi jsou vždy přesnější, protože udržujeme míru nejistoty a pravidelně vypočítáváme chybu mezi naší předpovědí a realitou. Jsme schopni z maticových násobení a pravděpodobnostních vzorců odhadnout rychlosti a polohy vozidel kolem nás.

“ Extended/Unscented “ filtry a nelinearita

vzniká zásadní problém. Naše matematické vzorce jsou implementovány s lineárními funkcemi typu y = ax + b.
Kalmanův filtr vždy pracuje s lineárními funkcemi. Na druhou stranu, když používáme Radar, data nejsou lineární.

Radar vidí svět s třemi opatření:

tyto tři hodnoty činí naše měření nelineární vzhledem k zahrnutí úhlu φ.

naším cílem je převést data ρ, φ, ρ na Kartézská data (px, py, vx, vy).

pokud do Kalmanova filtru zadáme nelineární data, náš výsledek již není v uni-modální Gaussově formě a již nemůžeme odhadnout polohu a rychlost.

Tak jsme se použít aproximace, což je důvod, proč pracujeme na dvě metody:
– Extended Kalman filtry, pomocí Jakobiho a Taylor série linearize model.
– Unscented Kalman filtry používají přesnější aproximaci linearizovat model.

řešit začlenění non linearity pomocí Radaru, techniky existují a umožňují naše filtry pro odhad polohy a rychlosti objektů, které chceme sledovat.