Rozdělení Pravděpodobnosti > Trojúhelníkové Rozdělení,

Co je Trojúhelníkové Rozdělení?

trojúhelníkové rozdělení (někdy nazývané rozdělení trojúhelníku) je spojité rozdělení pravděpodobnosti ve tvaru trojúhelníku. Je definován:

• a: minimální hodnota, kde a ≤ c
• c: maximální hodnota (výška trojúhelníku), kde a ≤ c ≤ b,
• b: maximální hodnota, kde b ≥ c.

to je velmi snadné odhadnout rozdělení parametrů z ukázkových dat:

• Použití vzorku minimálně jako odhad pro to,
• Použití vzorku maximální odhad pro b, a
• Použít jakékoliv rozumné statistiky (např. výběrový průměr, modus nebo medián) jako odhad pro c.

Pokud nemáte vzorek dat, expertní znalosti mohou být použity k odhadu pravděpodobné, minimální, maximální a nejpravděpodobnější hodnota (tj. režimu).

tři parametry, a b A c mění tvar trojúhelníku: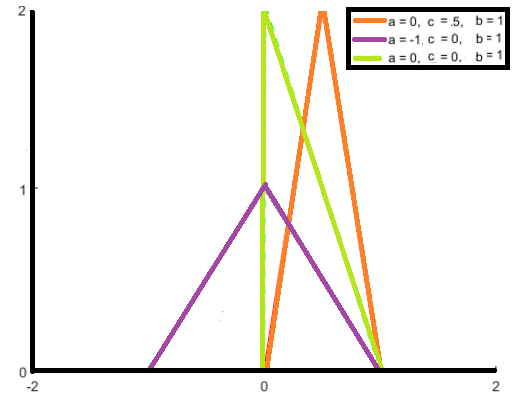

stejně jako všechny pravděpodobnostní rozdělení je plocha pod křivkou 1. Proto čím širší je vzdálenost mezi a A c (tj. rozsah), tím kratší je výška.

když je vrchol vystředěn na nulu a A = b, nazývá se symetrické trojúhelníkové rozdělení. Když se to stane, a a b jsou stejné, ale opačného znamení (např. -2, 2) a jsou někdy označovány jako -a a místo a a b.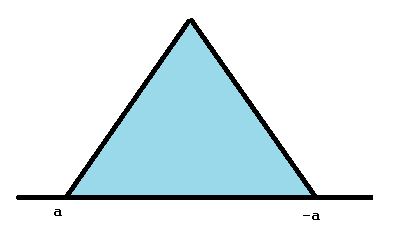

PDF, průměr a Směrodatná Odchylka

funkce hustoty pravděpodobnosti, která se používá k nalezení pravděpodobnosti náhodné veličiny spadá do určitého rozsahu, je dána tím, že: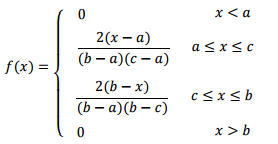

průměr pro toto rozdělení je:
μ = 1/3 (a + b + c).

směrodatná odchylka, s, je:
s = (1/√6).
Tento vzorec je předpoklad, že distribuce má střed v nule a koncové body jsou známé.

Odkaz:
Samuel Kotz, S. a van Dorp.J. (2004) Beyond Beta. Ukázková kapitola o rozdělení trojúhelníku je k dispozici zde od World Scientific.

——————————————————————————

Potřebujete pomoci s úkoly nebo zkoušky otázka? S Chegg Study, můžete získat krok za krokem řešení vašich otázek od odborníka v oboru. Váš první 30 minut s Chegg tutorem je zdarma!