nedílnou součástí dynamiky tekutin je vorticity. Heuristicky měří lokální rotaci tekutého pozemku. U pevných objektů nemluvíme o vířivosti objektu, ale místo toho odkazujeme na jeho úhlovou rychlost. Tyto dva pojmy spolu souvisejí, ale vorticita je užitečnější při diskusi o rotujících objektech, které se deformují, jako tekutina.

vířivost daného rychlostního pole v dané rovině se vypočítá výběrem dvou ortogonálních OS v této rovině a přidáním úhlové rychlosti každé osy. V pevný objekt nebo tekutina, která se otáčí jako pevný objekt (příhodně pojmenované pevné tělo, otáčení), vorticity je dvakrát úhlové rychlosti, protože každá osa se otáčí ve stejném poměru. V tekutině se však obě osy mohou otáčet velmi odlišnými rychlostmi a dokonce i různými směry! Je dokonce možné, že se každá osa může otáčet, ale čistá vířivost je nulová (viz irrotační vír).

Pokud pohyb tekutin je přísně omezena, aby ležet v rovině pak vektoru vorticity je přijata, aby bylo kolmé k rovině a nelze změnit směr (nebo tilt). Jediným aspektem vířivosti, který se může změnit, je její velikost. Předpokládá se, že tento přenos energie do větších měřítek je spojen s tvorbou velké červené skvrny na Jupiteru.

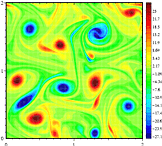
V trojrozměrném tekutiny pohybu vektoru vorticity je trojrozměrná v tom, že to má komponenty, vzájemně rovnoběžné osy, x, y a z: součást z je rovnoběžná s osou z a popisuje rychlost rotace v rovině xy. Je to kvůli této dichotomii, že existuje kvalitativní rozdíl v chování mezi dvourozměrnou turbulencí a trojrozměrnou turbulencí. V bývalém tam je tendence pro vírů se shlukují a vytvářejí větší vírů, vzhledem k tomu, že v druhé vírové pohyby jsou roztrhané od sebe a energetické kaskády dolů do nejmenších měřítek, kde je pak rozptýlené pryč.

Matematicky, vorticity daného rychlostního pole,

je definován tak, aby bylo zvlnění rychlostního pole, a je obvykle označeny řeckým písmenem omega,

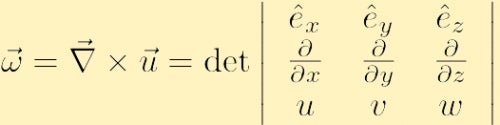
kde jsme použili konvenční nabla symbol pro gradient:

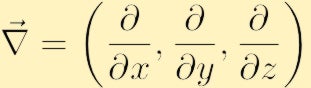
komponenta tvoří vorticity je nalézt tím, že rozšiřuje determinant výše,

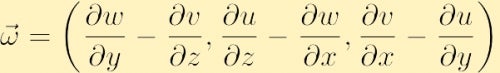
Dalším důležitým aspektem dynamiky tekutin, které souvisí s vorticity je krevní oběh. Na rozdíl od vorticity, která je lokální vlastností definovanou v každém bodě prostoru, je cirkulace globální vlastností definovanou integrací vlastnosti tekutiny přes křivku. Zejména, pokud si vyberete jakýkoli uzavřený obrys a označme jej písmenem C(t) oběh kolem C(t), ve směru hodinových ručiček, je skalární veličina označená s,

je definována jako,

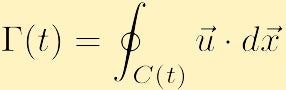
, který může být funkcí času, jako uzavřený obrys.

dovolte nám chvíli vysvětlit, co to říká fyzicky. V každém bodě na obrysu (t) najdeme složku rychlosti, která je tečná ke křivce a vynásobíme tuto skalární nekonečně malou délkou; promítání rychlosti na tečnu nutně poskytne velikost mezi rychlostí v této poloze a nulou. Pokud je rychlost tečná ke křivce, dostaneme plus nebo minus rychlost, pokud je rychlost kolmá ke křivce, dostaneme nulu. Pak integrujeme toto množství, jiný způsob, jak říci součet nekonečného počtu věcí, kolem obrysu, takže přidáme příspěvek z každého bodu. Z toho zjistíme, že cirkulace podél obrysu C (t) je množství toku kolem obrysu (t); pozitivní nebo negativní výsledek odpovídá obrysu ve směru hodinových ručiček nebo ve směru hodinových ručiček. Jeden extrémní případ je, kde rychlost pole je všude kolmá ke křivce C(t) a proto není oběhu, protože tok je vždy přes obrys a nikdy teče podél obrysu. Chcete-li získat nenulovou cirkulaci, musí existovat část křivky, kde je tok podél uzavřeného obrysu.

Pokud se rychlost pole je hladká a nejsou tam žádné singularity v C(t) pak můžeme použít Stokesovu Integrální Věty z vektorového počtu přepsat oběhu,

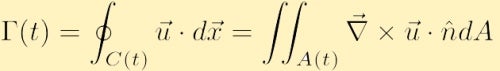
kde A je plocha obsažené v obrysu C a ń je jednotkový normálový vektor k areaA.

než uvažujeme o této nové rovnici pro oběh, je užitečné pochopit fyzický význam pro Stokesovu větu, kde vektorové pole je rychlost. Ve dvojitém integrálu výše vypočítáme vorticitu v každém bodě obrysu a pak shrneme vorticitu nad všemi těmito body V A (t). V jediném integrálu nad uzavřeným obrysem počítáme tok podél hranice oblasti. Stokes‘ věta pak uvádí, že tato množství jsou stejné, a proto, že pokud nemáme na mysli vorticity v prostoru, který pak musí znamenat oblasti má nenulovou rychlost otáčení, musí být proto čistý oběhu po obvodu hranice.

z věty o střední hodnotě počtu můžeme integrand v dvojitém integrálu nahradit střední hodnotou, která odpovídá střední složce vorticity kolmé k rovině, ve které leží C(t). Druhá interpretace oběhu tedy spočívá v tom, že se jedná o střední vorticitu krát plochu obsaženou v C (t). Místo výpočtu oběhu na uzavřenou křivku C(t) můžeme vypočítat střední vorticity normální A(t), a násobit, že oblast uvnitř. Pokud vezmete v úvahu zvláštní případ, kdy je vířivost všude konstantní, oběh by byl Velikost vířivosti krát oblast obsažená uvnitř.

bodový vír je vír, který nemá žádnou oblast, což znamená, že vírnost je přítomna pouze v jednom bodě. Pro studium bodových vírů nejprve předpokládáme, že máme 2D nestlačitelný tok. (Bodové víry jsou také někdy označovány jako přímkové víry při pohledu ve 3D.)

Po nějaké výpočty, zjistíme, že rychlostní pole, které je generované bod vír, v komplexní formě, která se nachází na z0 je dána vztahem (kde Gama je nula oběhu kolem bodu vír, který je často odkazoval se na jako síla v bodě vortex):

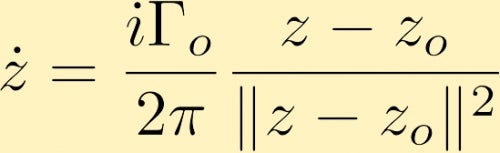
rychlostní pole vytvořené jedním bodem vír může způsobit další bod vortex pohybovat. Zde je několik příkladů: Dva bodové víry, pozitivní i stejné velikosti, dva bodové víry, oba pozitivní, ale jeden má trojnásobnou sílu druhého a jeden bodový vír je negativní s dvojnásobnou velikostí druhého, který je pozitivní . Další možností je zvážit dva bodové víry stejné velikosti, ale opačné znaménko.

to lze rozšířit na libovolný počet bodových vírů, N. rovnice pohybu v komplexní formě pro bodový vír alfa je dána:

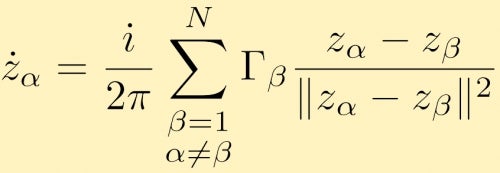
při Pohledu na interakce bod vírů je velmi zajímavý problém, který je obtížné dělat analyticky zejména jako číslo bodu vírů se zvyšuje. Numerické simulace interakcí bodových vírů jsou tedy velmi běžné. Jednou z užitečných aplikací velkých bodových vírových simulací je, když se podíváte na velké shluky bodových vírů, které simulují víry s konečnou plochou. Zde jsou popisy a výsledky několika velkých bodových vírových simulací. V tomto případě máme dvě velké shluky bodových vírů stejné síly. V dalším případě začneme kruhem seskupených bodových věrohodností.

abychom našli rovnici pro vývoj vorticity, začneme rovnicí hybnosti. V hybnosti rovnice advective výraz může být přepsán takto,

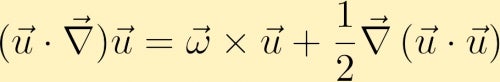
další výpočet zvlnění hybnosti rovnice a přes některé vektorové identity dostaneme rovnici vorticity:

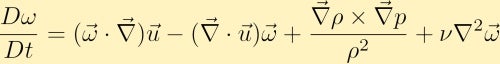
rovnice vorticity ukazuje, jak může být v tekutině generována vorticita. Bez ztráty obecnosti předpokládáme, že zpočátku máme pouze vorticitu ve směru z. Z toho můžeme vidět, jak každý ze čtyř různých termínů může změnit vorticitu.

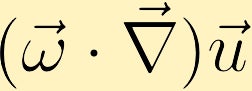
Pokud je změna v rychlosti se směrem od stávající vorticity, vorticity mohou být generovány.

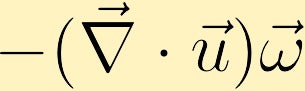
Pokud se tekutina pozemku se rozšiřuje a vorticity je pozitivní vorticity tekutiny pozemku bude klesat a v případě, že zásilka je smluvní vorticity zvýší.

Fluidní vrstvy konstantní hustoty (isopycnals) chci se shodují s vrstvami konstantní tlak (isobars). Pokud se tyto vrstvy neshodují, tekutina se začne otáčet, aby se vyrovnala, což způsobí generování vířivosti. (V příkladu začínáme nulovou vorticitou.)

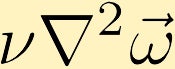
viskózní síly způsobují difúzi vířivosti. (V příkladu začínáme bodem nekonečné vířivosti ve středu.)