antenner udstråler elektromagnetisk energi til at transmittere eller modtage information. Derfor er udtrykkene energi og magt forbundet med disse elektromagnetiske bølger, og vi er nødt til at diskutere dem. En elektromagnetisk bølge har både elektriske og magnetiske felter.

overvej bølgen på ethvert tidspunkt, som kan ses i begge vektorer. Følgende figur viser repræsentationen af elektriske og magnetiske feltkomponenter i en elektromagnetisk bølge.

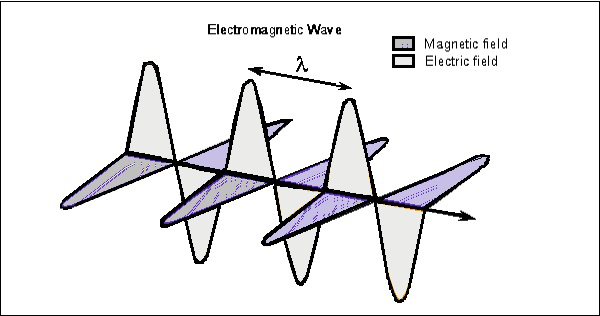
den elektriske bølge er til stede lodret til udbredelsen af EM-bølge, mens den magnetiske bølge er vandret placeret. Begge felter er vinkelret på hinanden.

Poynting Vector

Poynting vector beskriver energien i EM-bølgen pr. John Henry Poynting afledte først denne vektor i 1884, og derfor blev den opkaldt efter ham.

Definition − “Poynting-vektor giver energioverførselshastigheden pr.arealenhed”

eller

“den energi, som en bølge bærer pr. tidsenhed pr. arealenhed, gives af Poynting-vektoren.”

Poynting vector er repræsenteret af kr.

enheder

SI-enheden for Poynting-vektor er M/m2.

matematisk udtryk

den mængde, der bruges til at beskrive den effekt, der er forbundet med de elektromagnetiske bølger, er den øjeblikkelige Poynting-vektor, som er defineret som

$$\hat{s} = \hat{E} \times \hat{h}$$

hvor

• $\hat{S}$ er den øjeblikkelige Poynting-vektor (m / m2).

• $\hat{E}$ er den øjeblikkelige elektriske feltintensitet (V / m).

• $\hat{H}$ er den øjeblikkelige magnetfeltintensitet (a / m).

det vigtige punkt, der skal bemærkes her, er, at størrelsen af E er større end H inden for en EM-bølge. Men begge bidrager med samme mængde energi. Det er vektoren, som har både retning og størrelse. Kursen er den samme som bølgens hastighed. Dens størrelse afhænger af E og H.

afledning af Poynting vektor

for at få en klar ide om Poynting vektor, lad os gå igennem afledningen af denne Poynting vektor i en trinvis proces.lad os forestille os, at en EM-bølge passerer et område (A) vinkelret på H-aksen, langs hvilken bølgen bevæger sig. Mens den passerer gennem A, i uendelig lille tid (dt), bevæger bølgen en afstand (DKs).

$$$ = C\ dt$$

hvor

$$C = hastighed\ af\ lys = 3\gange 10^{8}m/s$$$$volumen, dv = AC\ dt$$$$ d\mu = \mu\ dv = (\epsilon_{0}e^{2})(AC\ dt)$$$$ = \epsilon_{0} AC \ E^{2}\ dt$$

derfor er energi overført i tid (dt) pr. Område (a) −

$ $ s= \frac{energi}{tid\gange område} = \frac{dt\ a} = \frac {\EPSILON_ {0} Ace^{2}\ dt} {dt\ a} = \epsilon_{0} C\:E^{2}$$

siden

$$ \ frac{e}{H} = \ frac {\mu_{0}} {\epsilon_{0}}\ derefter\ s= \frac{CB^{2}}{\mu_{0}}$$

siden

$$C = \frac{E}{H} \ derefter \ s = \frac{EB} {\mu_{0}}$$$$= \hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

liter betegner Poynting-vektoren.

ovenstående ligning giver os energien pr.tidsenhed, pr. arealenhed på et givet tidspunkt, som kaldes Poynting vektor.