Blog
i et tidligere blogindlæg diskuterede vi, hvordan supermarkeder bruger data til bedre at forstå forbrugernes behov og i sidste ende øge deres samlede forbrug. En af de vigtigste teknikker, der anvendes af de store detailhandlere, kaldes Market Basket Analysis (MBA), som afdækker sammenhænge mellem produkter ved at lede efter kombinationer af produkter, der ofte forekommer i transaktioner. Med andre ord giver det supermarkederne mulighed for at identificere forholdet mellem de produkter, som folk køber. For eksempel vil kunder, der køber en blyant og papir, sandsynligvis købe en gummi eller lineal.
“Markedskurvanalyse giver detailhandlere mulighed for at identificere forhold mellem de produkter, som folk køber.”
detailhandlere kan bruge den indsigt, der er opnået fra MBA på en række måder, herunder:
- gruppering af produkter, der forekommer sammen i designet af en butiks layout for at øge chancen for krydssalg;
- kørsel Online anbefalingsmotorer (“kunder, der købte dette produkt, har også set dette produkt”); og
- målretning af marketingkampagner ved at sende salgsfremmende kuponer til kunder for produkter relateret til varer, de for nylig har købt.
i betragtning af hvor populær og værdifuld MBA er, troede vi, at vi ville producere følgende trinvise vejledning, der beskriver, hvordan det virker, og hvordan du kan gå om at foretage din egen Markedskurvanalyse.
Hvordan fungerer Markedskurvanalyse?
for at udføre en MBA skal du først have et datasæt af transaktioner. Hver transaktion repræsenterer en gruppe af varer eller produkter, der er købt sammen og ofte omtalt som et “itemset”. For eksempel kan et varesæt være: {blyant, papir, hæfteklammer, gummi} i hvilket tilfælde alle disse varer er købt i en enkelt transaktion.
i en MBA analyseres transaktionerne for at identificere associeringsregler. For eksempel kan en regel være: {pencil, paper} => {rubber}. Det betyder, at hvis en kunde har en transaktion, der indeholder en blyant og papir, så vil de sandsynligvis være interesserede i også at købe en gummi.
før du handler efter en regel, skal en detailhandler vide, om der er tilstrækkelig dokumentation til at antyde, at det vil resultere i et gavnligt resultat. Vi måler derfor styrken af en regel ved at beregne følgende tre metrics (Bemærk andre metrics er tilgængelige, men disse er de tre mest almindeligt anvendte):
Support: procentdelen af transaktioner, der indeholder alle elementerne i et varesæt (f.eks. blyant, papir og gummi). Jo højere understøttelsen er, jo oftere forekommer varesættet. Regler med høj støtte foretrækkes, da de sandsynligvis vil gælde for et stort antal fremtidige transaktioner.
tillid: sandsynligheden for, at en transaktion, der indeholder elementerne på venstre side af reglen (i vores eksempel blyant og papir) også indeholder varen på højre side (en gummi). Jo højere tillid, jo større er sandsynligheden for, at varen på højre side vil blive købt, eller med andre ord, jo større returrate kan du forvente for en given regel.
løft: sandsynligheden for, at alle elementerne i en regel forekommer sammen (ellers kendt som understøttelsen) divideret med produktet af sandsynlighederne for elementerne på venstre og højre side, som om der ikke var nogen sammenhæng mellem dem. For eksempel, hvis blyant, papir og gummi forekom sammen i 2,5% af alle transaktioner, blyant og papir i 10% af transaktionerne og gummi i 8% af transaktionerne, ville elevatoren være: 0.025/(0.1*0.08) = 3.125. En lift på mere end 1 antyder, at tilstedeværelsen af blyant og papir øger sandsynligheden for, at en gummi også vil forekomme i transaktionen. Samlet set opsummerer lift styrken af forbindelsen mellem produkterne på venstre og højre side af reglen; jo større lift jo større er forbindelsen mellem de to produkter.
for at udføre en Markedskurvanalyse og identificere potentielle regler bruges en data mining-algoritme kaldet ‘Apriori-algoritmen’ ofte, som fungerer i to trin:
- Identificer systematisk varesæt, der ofte forekommer i datasættet med en understøttelse, der er større end en forud specificeret tærskel.
- Beregn tilliden til alle mulige regler i betragtning af de hyppige varesæt, og hold kun dem med en tillid, der er større end en forud specificeret tærskel.
tærsklerne for at indstille support og tillid er brugerspecificerede og vil sandsynligvis variere mellem transaktionsdatasæt. R har standardværdier, men vi anbefaler, at du eksperimenterer med disse for at se, hvordan de påvirker antallet af returnerede regler (mere om dette nedenfor). Endelig, selvom Apriori-algoritmen ikke bruger lift til at etablere regler, vil du se i det følgende, at vi bruger lift, når vi udforsker de regler, som algoritmen returnerer.
udførelse af Markedskurvanalyse i R
for at demonstrere, hvordan man udfører en MBA, har vi valgt at bruge R og især arules-pakken. For dem, der er interesserede, har vi inkluderet Den R-kode, som vi brugte i slutningen af denne blog.
Her følger vi det samme eksempel, der bruges i Arulesvis-vignetten, og bruger et datasæt med købmandssalg, der indeholder 9.835 individuelle transaktioner med 169 varer. Den første ting, vi gør, er at se på punkterne i transaktionerne og især plotte den relative frekvens af de 25 hyppigste poster i Figur 1. Dette svarer til understøttelsen af disse elementer, hvor hvert elementsæt kun indeholder det enkelte element. Denne bar plot illustrerer de dagligvarer, der ofte købes i denne butik, og det er bemærkelsesværdigt, at støtten til selv de hyppigste varer er relativt lav (for eksempel forekommer den hyppigste vare kun i omkring 2,5% af transaktionerne). Vi bruger disse indsigter til at informere minimumsgrænsen, når du kører Apriori-algoritmen; for eksempel ved vi, at for at algoritmen skal returnere et rimeligt antal regler, skal vi indstille støttetærsklen til et godt stykke under 0.025.
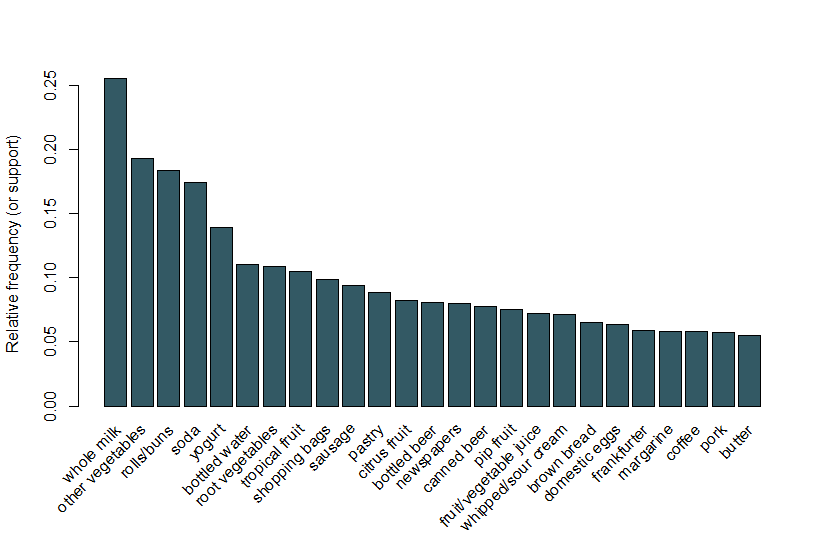
Figur 1 en bar plot af understøttelsen af de 25 hyppigste købte varer.
Ved at indstille en støttetærskel på 0,001 og tillid på 0,5 kan vi køre Apriori-algoritmen og opnå et sæt på 5.668 resultater. Disse tærskelværdier vælges således, at antallet af returnerede regler er højt, men dette tal ville reducere, hvis vi øgede en af tærsklerne. Vi vil anbefale at eksperimentere med disse tærskler for at opnå de mest passende værdier. Mens der er for mange regler til at kunne se på dem alle individuelt, kan vi se på de fem regler med den største lift:
| regel | Support | tillid | Lift | |
| {instant food products,soda}=>{hamburger meat} | 0.001 | 0.632 | 19.00 | |
| {soda, popcorn}=> {Salty snacks} | 0.001 | 0.632 | 16.70 | |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 | |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 | |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. For eksempel kan den første regel repræsentere den slags varer, der er købt til en grill, den anden til en filmaften og den tredje til bagning.
i stedet for at bruge tærsklerne til at reducere reglerne ned til et mindre sæt, er det normalt, at et større sæt regler returneres, så der er større chance for at generere relevante regler. Alternativt kan vi bruge visualiseringsteknikker til at inspicere det regelsæt, der returneres, og identificere dem, der sandsynligvis vil være nyttige.
Ved hjælp af arulesvis-pakken plotter vi reglerne ved tillid, støtte og løft i figur 2. Dette plot illustrerer forholdet mellem de forskellige målinger. Det har vist sig, at de optimale regler er dem, der ligger på det, der er kendt som “support-tillidsgrænsen”. I det væsentlige er dette reglerne, der ligger på plotens højre kant, hvor enten støtte, tillid eller begge maksimeres. Plotfunktionen i arulesvis-pakken har en nyttig interaktiv funktion, der giver dig mulighed for at vælge individuelle regler (ved at klikke på det tilknyttede datapunkt), hvilket betyder, at reglerne på grænsen let kan identificeres.
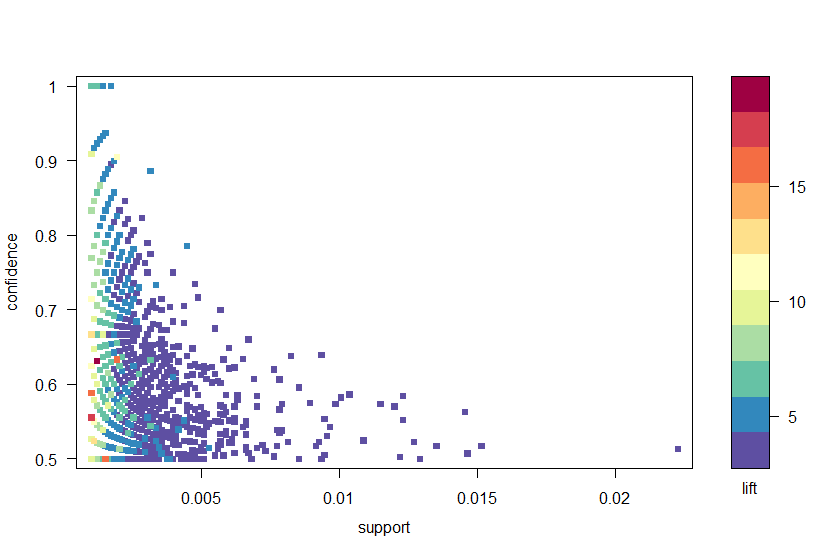
figur 2: en scatter plot af tillid, støtte og løft målinger.
der er mange andre plot til rådighed for at visualisere reglerne, men en anden figur, som vi vil anbefale at udforske, er den grafbaserede visualisering (se figur 3) af de ti bedste regler med hensyn til lift (du kan inkludere mere end ti, men disse typer grafer kan let blive rodet). I denne graf repræsenterer de elementer, der er grupperet omkring en cirkel, et varesæt, og pilene angiver forholdet i regler. For eksempel er en regel, at køb af sukker er forbundet med køb af mel og bagepulver. Størrelsen på cirklen repræsenterer det konfidensniveau, der er forbundet med reglen, og farven løfteniveauet (jo større cirkel og jo mørkere den grå, jo bedre).
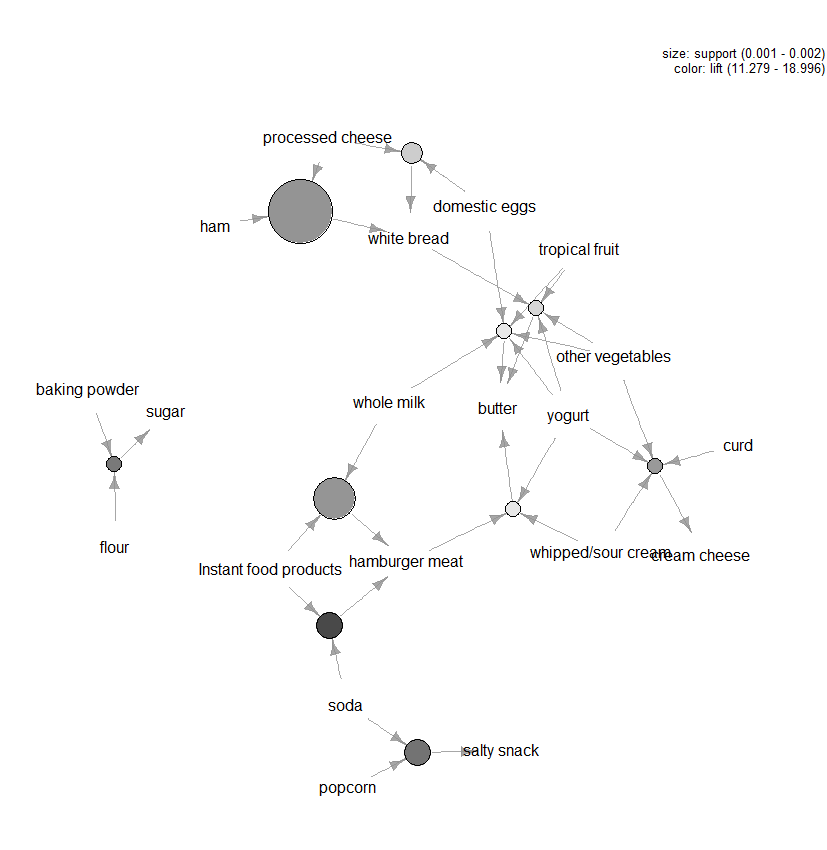
figur 3: grafbaseret visualisering af de ti bedste regler med hensyn til løft.
Markedskurvanalyse er et nyttigt værktøj til detailhandlere, der ønsker bedre at forstå forholdet mellem de produkter, som folk køber. Der er mange værktøjer, der kan anvendes, når du udfører MBA, og de vanskeligste aspekter ved analysen er at sætte tillid og støttetærskler i Apriori-algoritmen og identificere, hvilke regler der er værd at forfølge. Typisk gøres sidstnævnte ved at måle reglerne med hensyn til målinger, der opsummerer, hvor interessante de er, ved hjælp af visualiseringsteknikker og også mere formelle multivariate statistikker. I sidste ende er nøglen til MBA at udtrække værdi fra dine transaktionsdata ved at opbygge en forståelse af dine forbrugers behov. Denne type information er uvurderlig, hvis du er interesseret i marketingaktiviteter såsom krydssalg eller målrettede kampagner.
Hvis du gerne vil vide mere om, hvordan du analyserer dine transaktionsdata, bedes du kontakte os, og vi hjælper gerne.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.