brydning eller bøjning af lys forekommer, når lys passerer fra et medium til et andet medium med et andet brydningsindeks. Brydning er et vigtigt kendetegn ved linser, der giver dem mulighed for at fokusere en lysstråle på et enkelt punkt og er også ansvarlig for en række velkendte fænomener, såsom den tilsyneladende forvrængning af genstande, der delvist er nedsænket i vand.

brydningsindeks defineres som den relative hastighed, hvormed lys bevæger sig gennem et materiale med hensyn til dets hastighed i et vakuum. Ved konvention defineres brydningsindekset for et vakuum som en værdi på 1,0. Brydningsindekset, n, for andre gennemsigtige materialer defineres gennem ligningen:

hvor c er lysets hastighed, og v er lysets hastighed i dette materiale. Da brydningsindekset for et vakuum er defineret som 1.0 og et vakuum er blottet for ethvert materiale, brydningsindekserne for alle gennemsigtige materialer er derfor større end 1,0. Til de fleste praktiske formål kan brydningsindekset for lys gennem luft (1.0003) bruges til at beregne brydningsindekser for ukendte materialer. Brydningsindekser for nogle almindelige materialer er vist i tabel 1 nedenfor.

materiale brydningsindeks luft 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. For eksempel, når lys passerer fra et mindre tæt medium, såsom luft, til et mere tæt medium, såsom vand, falder den hastighed, hvormed den elektromagnetiske bølge bevæger sig. Alternativt, når lyset passerer fra et mere tæt medium til et mindre tæt medium, øges bølgens hastighed.

den vinkel, hvormed brydet lys bevæger sig, afhænger imidlertid af både indfaldsvinklen og sammensætningen af det materiale, som det kommer ind i. Det normale kan defineres som en linje vinkelret på grænsen mellem to stoffer. Lys passerer ind i grænsen i en vinkel til det normale og brydes i henhold til Snells lov:

hvor n repræsenterer brydningsindekserne for materiale 1 og materiale 2 og K symboliserer lysets vinkler, der bevæger sig gennem disse materialer med hensyn til det normale. Der er flere vigtige punkter, der kan trækkes fra denne ligning. Når n(1) er større end n (2), er brydningsvinklen altid mindre end indfaldsvinklen. Alternativt, når n(2) er større end n (1), er brydningsvinklen altid større end indfaldsvinklen. Når de to brydningsindekser er ens (n(1) = n(2)), føres lyset igennem uden brydning.

begrebet brydningsindeks er illustreret i Figur 1 nedenfor med fokus på tilfældet med lys, der passerer fra luft gennem både glas og vand. Bemærk, at mens begge bjælker kommer ind i det tættere materiale gennem den samme indfaldsvinkel i forhold til det normale (60 grader), er brydningen for glas næsten 6 grader større end for vand på grund af det højere brydningsindeks for glas.

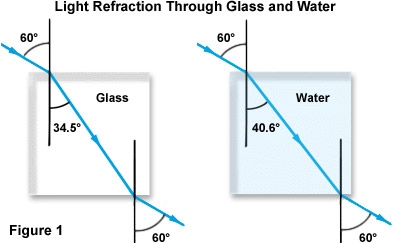
forskere har fundet, at brydningsindekset varierer med frekvensen af stråling (eller bølgelængde) af lys. Dette fænomen forekommer i forbindelse med alle gennemsigtige medier og er blevet betegnet dispersion. Derfor skal den særlige bølgelængde, der anvendes i målingen, identificeres ved måling af brydningsindekset for et gennemsigtigt stof. Nedenfor beskriver tabel 2 spredningen af tre uafhængige bølgelængder i forskellige medier.

materiale blå (486,1 nm) gul (589,3 nm) rød (656,3 nm) kronglas 1.524 1.517 1.515 flintglas 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Dette lys kaldes D-linjespektrumog repræsenterer det gule lys, der er anført i tabel 2 ovenfor. Ligeledes svarer f-linje-og C-linjespektre til blåt og rødt lys med specifikke bølgelængder udsendt af brint. Disse spektre er grundlæggende i beregningen af dispersion, som kan defineres kvantitativt som:

hvor n er brydningsindekset for materialet ved en bestemt bølgelængde udpeget af D, F og C, som repræsenterer spektrallinierne, og hvor n er brydningsindekset for materialet ved en bestemt bølgelængde udpeget af D, F og C, som repræsenterer de spektrale linjer af natrium og hydrogen som beskrevet ovenfor. Forholdet er sådan, at når lysets bølgelængde stiger, falder brydningsindekset. Imidlertid spiller mange faktorer en rolle i dispersionen af forskellige materialer, herunder deres elementære og molekylære sammensætning. Flere uorganiske faste stoffer, såsom kromater, dichromater, cyanider, vanadater og halogenidkomplekser, har usædvanligt høje dispersioner. Alligevel kan organiske substituenter også bidrage til høj dispersion.

	Interactive Java Tutorial
brydning af lys Opdag, hvordan bølgelængden og indfaldende lysvinkel påvirker brydning i en række medier med forskellige brydningsindekser.

Refraction of light is particularly important in the construction and physics of lenses. Husk, at når lysstrålen forlod både glasset og vandet i Figur 1, blev den igen brudt i samme vinkel, som den kom ind i materialet. Dette koncept er afgørende for linsernes funktion, selvom linsens form påvirker det resulterende billede væsentligt. I en konveks linse, som illustreret nedenfor i figur 2, bøjes lysbølger reflekteret fra objektet, i dette tilfælde en giraf, mod linsens optiske centrum og konvergerer på brændpunktet.

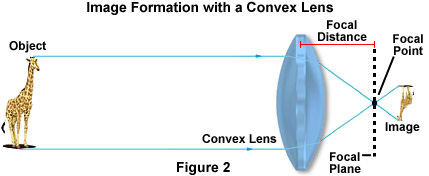
objektets relative position i forhold til linsens forreste fokuspunkt bestemmer, hvordan objektet afbildes. Hvis objektet er ud over dobbelt så lang som brændpunktet, ser det ud til at være mindre og omvendt og skal afbildes af en ekstra linse for at forstørre størrelsen. Men når billedet er tættere på linsen end brændpunktet, vises billedet lodret og større, som det let kan demonstreres med et simpelt forstørrelsesglas.

	Interactive Java Tutorial
billedforstørrelse Udforsk, hvordan billedet af en giraf forstørres ved brydning af lysbølger, der passerer gennem en simpel tynd bi-konveks linse.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Et simpelt drikkestrå i et glas fyldt med vand, som illustreret i figur 3, er et godt eksempel på denne forekomst. I dette eksempel skal lysbølger først passere gennem vandet, derefter gennem glas / vandgrænsen og til sidst gennem luften. Lysbølgerne, der reflekteres fra halmens ender, brydes i større grad end dem, der kommer fra halmens centrum, hvilket får halmen til at virke forstørret og let forvrænget.

det samme fænomen kan bruges til at bestemme brydningsindekset for en væske med et optisk mikroskop. For at gøre dette skal en flad celle, der er i stand til at holde væske med et mærke (eller gradueringer), placeres på den indvendige glasoverflade. Også, et af mikroskopets okularer skal have en gradueret reticle indsat i det primære billedplan til linjebreddemålinger af mærket i den flade celle. Før du tilføjer væsken med ukendt brydningsindeks til cellen, skal mikroskopet fokuseres på mærket i bunden af cellen og en måling af markens position på retiklen noteret. Dernæst skal der tilsættes en lille mængde væske til cellen, og mikroskopet fokuseres igen på mærket (gennem væsken) og en ny måling taget. Mikroskopet skal derefter endelig fokuseres på væskens overflade, og en tredje læsning registreres ved at måle positionen af mærket på retiklen. Brydningsindekset for den ukendte væske kan derefter beregnes ved hjælp af følgende ligning:

hvor D(målt) er den målte dybde (fra væskens overflade til positionen af mærket på den tomme celle) ved hjælp af mikroskopet, og D(tilsyneladende) er markeringsmålingen med og uden væske.

den kritiske refleksionsvinkel er et andet nøglebegreb i studiet af lysbrydning og er illustreret nedenfor i figur 4. Når lys passerer gennem et medium med højt brydningsindeks til et medium med lavere brydningsindeks, bliver lysbølgernes indfaldende vinkel en vigtig faktor. Hvis indfaldsvinklen stiger forbi en bestemt værdi (afhængig af brydningsindekset for de to medier), når den et punkt, hvor vinklen er så stor, at intet lys brydes ind i mediet med lavere brydningsindeks.

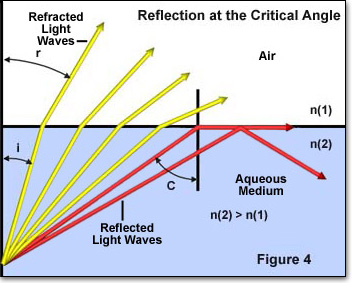
i figur 4 er individuelle lysstråler repræsenteret af enten røde eller gule farvede pile, der bevæger sig fra et medium med højt brydningsindeks (n(2)) til et af lavere brydningsindeks (n(1)). Indfaldsvinklen for hver enkelt lysstråle betegnes med i og brydningsvinklen med r. de fire gule lysstråler har alle en indfaldsvinkel (i), der er lav nok til at passere gennem grænsefladen mellem de to medier. De to røde lysstråler har imidlertid indfaldende vinkler, der overstiger den kritiske vinkel (cirka 41 grader) og reflekteres enten i grænsen mellem mediet eller tilbage i det høje brydningsindeksmedium. Dette fænomen finder sted, når brydningsvinklen (vinkel r i figur 4) bliver lig med 90 grader, og Snells lov reduceres til:

hvor (k) nu betegnes den kritiske vinkel C. Hvis mediet med mindre brydningsindeks er luft (n = 1.00) reduceres ligningen yderligere til:

som tidligere diskuteret er et andet vigtigt træk ved lysbrydning, at lysets bølgelængde har indflydelse på mængden af brydning, der forekommer inden for et medium. Faktisk er mængden af brydning, der finder sted, omvendt proportional med bølgelængden af det indfaldende lys. Således brydes kortere bølgelængde synligt lys i en større vinkel end længere bølgelængdelys. Følgelig, når hvidt lys, som er sammensat af alle farverne i det synlige spektrum, føres gennem et glasprisme, spredes det i dets komponentfarver på en måde, der er afhængig af de individuelle bølgelængder. Lavfrekvent synligt lys (600 nanometer og større) brydes i en mindre vinkel end lys med højere frekvens, hvilket resulterer i en regnbuelignende effekt, som illustreret nedenfor i figur 5.

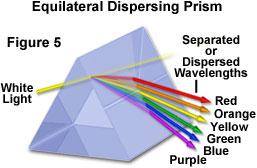
det samme fænomen er også ansvarlig for kromatisk aberration. Når hvidt lys føres gennem en simpel konveks linse, opstår der flere fokuspunkter i nærheden, der svarer til de mindre brydningsindeksforskelle i komponentbølgelængderne. Denne effekt har tendens til at producere farvede (enten røde eller blå, afhængigt af fokus) glorier omkring billeder af objekter. Korrektion af denne aberration opnås normalt ved anvendelse af kombinationer af to eller flere linseelementer sammensat af materialer med forskellige dispersive egenskaber, såsom en akromatisk linse konstrueret med både krone-og flintbriller.

	Interactive Java Tutorial
brydning af et prisme Undersøg, hvordan hvidt lys adskilles i dets komponentfarver ved brydning gennem forskellige vinkler i et prisme.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. Det mest almindelige eksempel er et kamera, der er designet til at skabe skarpe og fokuserede billeder på en emulsion af film eller overfladen på en ladekoblet enhed (CCD) for at producere et nøjagtigt billede. Andre optiske enheder, der udnytter disse egenskaber ved lys, inkluderer mikroskoper og teleskoper, som muliggør visning af objekter, der er usynlige for det blotte menneskelige øje, uanset om de er placeret på hovedet af en stift eller i en fjern galakse.

bidragende forfattere

Mortimer – Olympus America, Inc., To Corporate Center Drev., Melville, 11747.

Shannon H. Neaves og Michael Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Florida State University, Tallahassee, Florida, 32310.

Tilbage til lys og farve

spørgsmål eller kommentarer? Send os en mail.

krit 1998-2021 af Michael Davidson og Florida State University. Alle Rettigheder Forbeholdes. Ingen billeder, grafik, scripts eller applets må gengives eller bruges på nogen måde uden tilladelse fra indehaverne af ophavsretten. Brug af denne hjemmeside betyder, at du accepterer alle de juridiske vilkår og betingelser, der er angivet af ejerne.

denne hjemmeside vedligeholdes af vores
Graphics& programmering Team
i samarbejde med optisk mikroskopi på
National High Magnetic Field Laboratory.

sidste ændring:fredag, November 13, 2015 på 02:18 PM

adgang tæller siden marts 10, 2003: 181405

besøg hjemmesider vores partnere i uddannelse: