Kalman-filtre

algoritmen, der bruges til at flette dataene, kaldes et Kalman-filter.

Kalman-filteret er en af de mest populære algoritmer inden for datafusion. Opfundet i 1960 af Rudolph Kalman, bruges det nu i vores telefoner eller satellitter til navigation og sporing. Den mest berømte brug af filteret var under Apollo 11-missionen for at sende og bringe besætningen tilbage til månen.

Hvornår skal man bruge et Kalman-Filter ?

et Kalman-filter kan bruges til datafusion til at estimere tilstanden af et dynamisk system (udvikler sig med tiden) i nutiden (filtrering), fortiden (udjævning) eller fremtiden (forudsigelse). Sensorer indlejret i autonome køretøjer udsender foranstaltninger, der undertiden er ufuldstændige og støjende. Sensorernes unøjagtighed (støj) er et meget vigtigt problem og kan håndteres af Kalman-filtre.

et Kalman-filter bruges til at estimere tilstanden af et system, betegnet h. denne vektor er sammensat af en position p og en hastighed v.

Ved hvert skøn forbinder vi et mål for usikkerhed P.

ved at udføre en fusion af sensorer tager vi hensyn til forskellige data for det samme objekt. En radar kan estimere, at en fodgænger er 10 meter væk, mens Lidar estimerer, at den er 12 meter. Brugen af Kalman-filtre giver dig mulighed for at få en præcis ide at bestemme, hvor mange meter der virkelig er fodgængeren ved at eliminere støj fra de to sensorer.

et Kalman-filter kan generere estimater af tilstanden af objekter omkring det. For at foretage et skøn behøver det kun de aktuelle observationer og den tidligere forudsigelse. Målehistorikken er ikke nødvendig. Dette værktøj er derfor let og forbedres med tiden.

hvordan det ser ud

stat og usikkerhed er repræsenteret af Gaussere.

en gaussisk er en kontinuerlig funktion, under hvilken området er 1. Dette giver os mulighed for at repræsentere sandsynligheder. Vi er på en sandsynlighed for normalfordeling. Uni-modaliteten af Kalman-filtre betyder, at vi har en enkelt top hver gang for at estimere systemets tilstand.

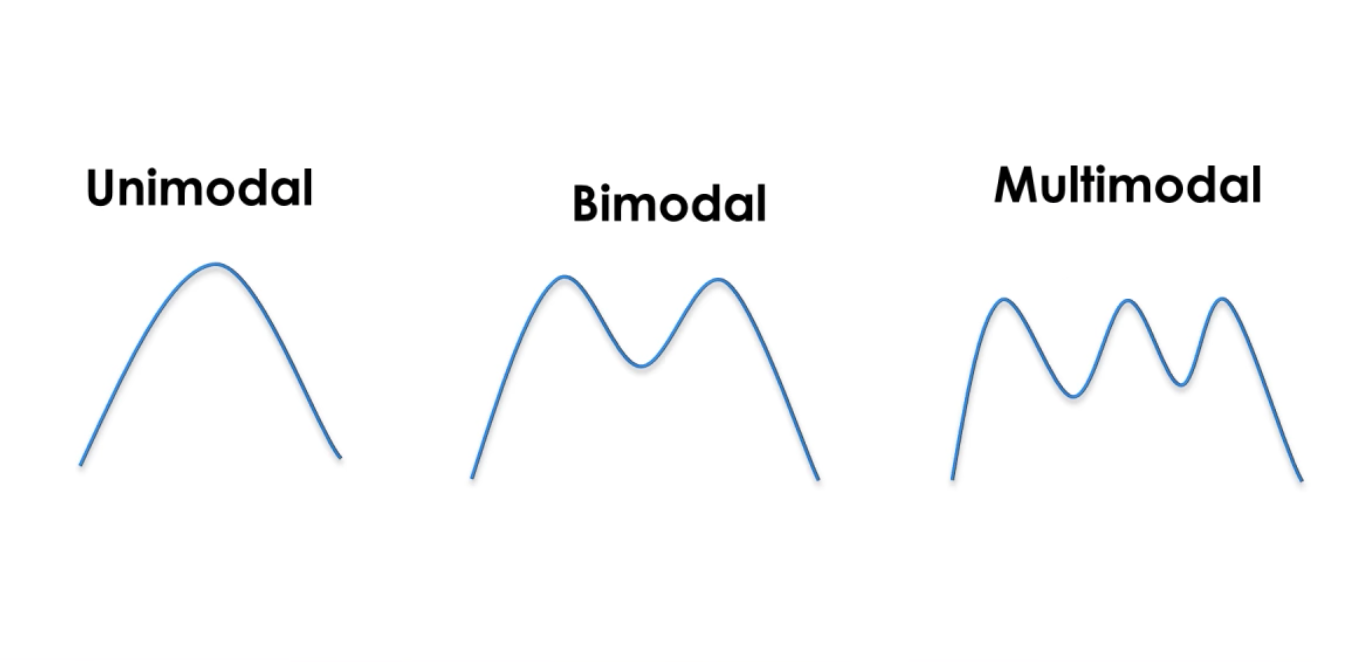
Vi har en gennemsnitlig LR, der repræsenterer en tilstand og en varians LR2, der repræsenterer en usikkerhed. Jo større variansen er, desto større er usikkerheden.

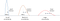
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Vi bruger observationer fra vores sensorer til at korrigere den forudsagte tilstand og opnå et mere nøjagtigt skøn.

for at foretage et skøn behøver et Kalman-filter kun aktuelle observationer og den tidligere forudsigelse. Målehistorikken er ikke nødvendig.

matematik

matematikken bag Kalman-filtre er lavet af tilføjelser og multiplikationer af matricer. Vi har to faser: forudsigelse og opdatering.

forudsigelse
vores forudsigelse består i at estimere en tilstand h’ og en usikkerhed P’ på tidspunktet t fra de tidligere tilstande h og P på tidspunktet t-1.

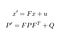
• f: overgangsmatrice fra T-1 til T
• larit: støj tilføjet
• k:
  

  

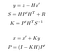
  • y: forskel mellem Faktisk måling og forudsigelse, dvs.fejlen.
  • S: estimeret systemfejl
  • H: Matrice for overgang mellem sensorens markør og vores.
  • R: Kovariansmatrice relateret til sensorstøj (givet af sensorproducenten).
  • K: Kalman gevinst. Koefficient mellem 0 og 1 afspejler behovet for at rette vores forudsigelse.

  opdateringsfasen gør det muligt at estimere en H og en P tættere på virkeligheden end hvad målingerne giver.

  et Kalman-filter tillader forudsigelser i realtid uden data på forhånd. Vi bruger en matematisk model baseret på multiplikation af matricer for hver gang, der definerer en tilstand H (position, Hastighed) og usikkerhed P.

  genoptrykning Prior/Posterior

  dette diagram viser, hvad der sker i et Kalman-filter.

  

  • forudsagt tilstandsestimat repræsenterer vores første skøn, vores forudsigelsesfase. Vi taler om prior.
  • måling er måling fra en af vores sensorer. Vi har bedre usikkerhed, men sensorernes støj gør det til en måling, der altid er vanskelig at estimere. Vi taler om sandsynlighed.
  • Optimal Tilstandsestimat er vores opdateringsfase. Usikkerheden er denne gang den svageste, vi akkumulerede information og fik lov til at generere en værdi mere sikker end med vores sensor alene. Denne værdi er vores bedste gæt. Vi taler om posterior.

  hvad et Kalman-filter implementerer er faktisk en Bayes-regel.

  

  i et Kalman-filter løber vi forudsigelser fra målinger. Vores forudsigelser er altid mere præcise, da vi holder et mål for usikkerhed og regelmæssigt beregner fejlen mellem vores forudsigelse og virkelighed. Vi er i stand til fra matricer multiplikationer og sandsynlighedsformler at estimere hastigheder og positioner af køretøjer omkring os.

  ” udvidede/Unscented ” filtre og ikke-linearitet

  et væsentligt problem opstår. Vores matematiske formler implementeres alle med lineære funktioner af type y = økse + b.
  et Kalman-filter fungerer altid med lineære funktioner. På den anden side, når vi bruger en Radar, er dataene ikke lineære.

  

  radaren ser verden med tre mål:

  disse tre værdier gør vores måling til en ikke-lineær i betragtning af inkluderingen af vinklen.

  vores mål her er at konvertere data til Cartesian data (PK, py, VK, vy).

  Hvis vi indtaster ikke-lineære data i et Kalman-filter, er vores resultat ikke længere i uni-modal Gaussisk form, og vi kan ikke længere estimere position og hastighed.

  så vi bruger tilnærmelser, hvorfor vi arbejder på to metoder:
  – udvidede Kalman-filtre bruger Jacobian og Taylor-serien til at linearisere modellen.
  – uparfumerede Kalman-filtre bruger en mere præcis tilnærmelse til at linearisere modellen.

  for at håndtere inkluderingen af ikke-linearitet ved radaren findes teknikker og tillader vores filtre at estimere position og hastighed for de objekter, vi ønsker at spore.