the Revolutionary Galois Theory

den 31.maj 1832 døde en fransk republikansk revolutionær, der blev kaldt Krisvariste Galois, af et skud. Han var 20 år gammel. Natten før, af frygt for sin egen død, havde Galois skrevet mange breve og frenetisk skrevet “Jeg har ingen tid; jeg har ingen tid”. Et bogstav er især værdifuldt af historiske grunde. I dette brev hævder Galois at have faktisk udløst revolutionen. Ikke en politisk. Men en matematisk.
for at romantisere endnu mere historien om Galois ‘ dramatiske liv, her er et abstrakt af en dokumentar, jeg lavede om algebra:

han er bestemt! Men hans matematiske revolution gik ikke glat. Som enhver revolutionsleder havde han først de største vanskeligheder. Ikke at forestille sig revolutionen. Men for at overbevise andre om at slutte sig til ham i en spilændrende tilgang til matematik. Da Galois stadig var i LIVE, blev hans revolutionære ideer afvist flere gange af det franske videnskabsakademi… fordi de bedste franske matematikere på den tid som Sim porron Denis Poisson bare ikke kunne få det! Dels på grund af Galois’ ulæselige håndskrift vist til højre…
i 1843, 10 år efter Galois’ død, lykkedes det endelig en strålende fransk matematiker ved navn Joseph Liouville at forstå nogle af Galois’ ideer. Efter yderligere 3 års arbejde offentliggjorde Liouville en artikel for at forklare dem. Men Liouville ‘ s artikel var stadig for langt ude for andre matematikere at nyde og forstå. Det tog yderligere 24 år at finde en fransk matematiker fremragende nok til bedre at forstå Galois og gøre hans ideer halte. Denne fremragende matematiker er Camille Jordan. Faktisk var Jordans 1870-bog om Galois-teorien så velskrevet, at den tyske matematiker Feliks Klein fandt den så læsbar som en tysk bog!
det var bestemt et kæmpe løft. Men det ville tage yderligere 82 år for den store østrigske matematiker Emil Artin endelig at give Galois-teorien sin moderne form i 1942. Artin fortjener mange kreditter. Mens Galois var den visionære, der forudså denne revolution, er Artin i mange sanser den, der faktisk foretog revolutionen og væltede matematik. Takket være Artin, og et par andre, i dag, Galois teori er blevet en uundgåelig hjørnesten i forskning i matematik, med masser af overraskende og fantastiske resultater (ligesom viles’ bevis for Fermat sidste sætning), samt et stort reservoir af åbne spørgsmål og mysterier!
felter i ren Algebra
Galois teori handler om symmetrier af tal. Men før jeg kommer derhen, skal jeg introducere dig for at få dig bevæbnet ved at lade dig på en hemmelighed om tal. Og jeg er sikker på, at du har hørt om det! Faktisk, tilbage i gymnasiet, blev du sandsynligvis lært aldrig at forlade rødder i nævnerne.
Jeg mener, at $1 / (\kvm{2}-1)$ ikke var et rigtigt svar. Kan du hjælpe med at slippe af med kvadratroden af 2 i nævneren?
Hehe… vi blev lært at formere sig op og ned med nævnerens konjugat. Dette konjugat opnås ved at erstatte $-$ med $+$ (eller omvendt) i nævneren:
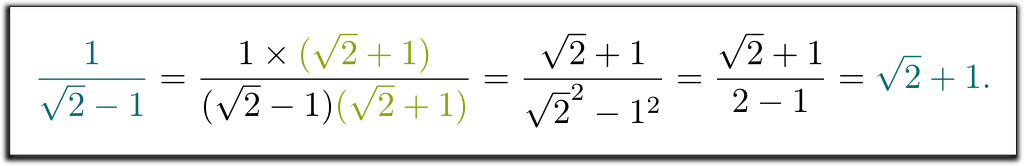
Jeg ved det! Det komplicerede udtryk $1 / ($2}-1) $ repræsenterer det samme tal som $${2}+1$. Og dette forklarer, hvorfor vores lærere ønskede, at vi skulle skrive resultater på den ene måde snarere end den anden: når alt er skrevet på samme måde, bliver eksamener meget lettere at rette!
men hvad med $1 / (\kvm{2}-1)$? Kan du slippe af med roden i nævneren? Kan det endda gøres?
Jeg ved det!
du fortæller mig!
noget held?
Hehe… interessant nok kan enhver magt på $\kvm{2}-1$ skrives som en sum af beføjelser på $\kvm{2}$. Faktisk skal du bare distribuere produkterne:
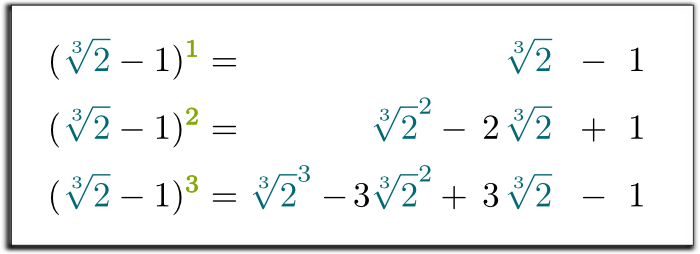
Ja det er det! Ved at gøre denne substitution i den tredje ligning har vi vist, at de tre første kræfter på $\kvm{2}-1$ kan skrives som en sum af et rationelt tal, på $\kvm{2}$ og på $\kvm{2}^2$!
så vi har nu 3 ligninger, med 2 rodudtryk, vi vil slippe af med! Således kan vi kombinere ligningerne for at fjerne alle rodudtryk til højre!
lad os multiplicere de 2 første linjer med 3 og tilføje alle 3 ligninger:
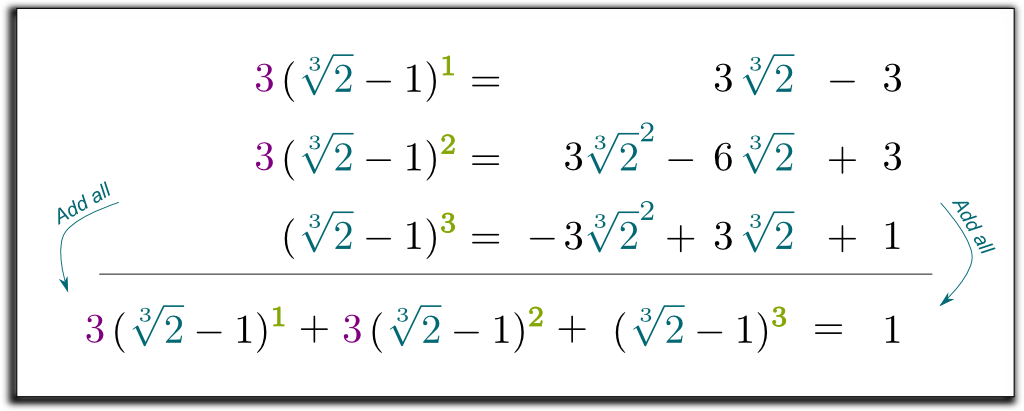
Hehe… det seje er, at det venstre udtryk, vi har opnået, nu kan faktoriseres med $\kvm{2}-1$! Lad mig springe over nogle kedelige beregninger… og komme til resultatet $(\kvm{2}-1)$ $(\kvm{2}^2 + \ kvm{2} + 1)$ $= 1$. Så for at slippe af med rødderne i nævneren kan vi multiplicere op og ned med $\kvm{2}^2 + \kvm{2} + 1$! Endelig får vi følgende overraskende og smukke formel:
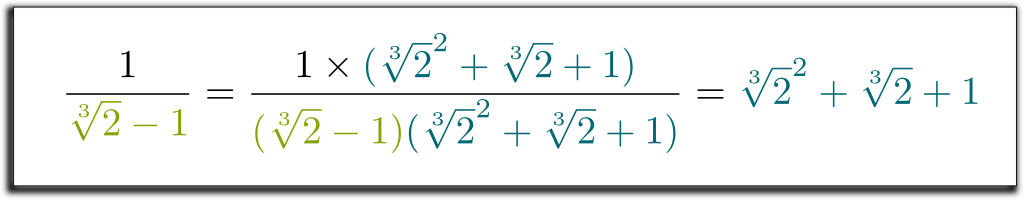
Jeg ved det! Men hvad der er endnu pænere er, at den metode, vi brugte, er meget generel! Med lignende teknik kan vi nu fjerne alle radikaler fra nævnere!
nu var det, der var af særlig interesse for Galois, ikke det faktum, at en metode gjorde det muligt at fjerne radikaler fra nævnere. Men snarere, at ethvert tal med radikaler i nævnere svarede til et tal med radikaler på toppen. Dette betød, at tallene med radikaler på toppen var stabile ved division.
det er almindeligt at betegne $ \ mathbb med{2}]$ det sæt tal, der kan skrives som en sum af kræfter på $\kvm{2}$. Da $ \ kvadratt{2}^3 = 2$ er et rationelt tal, kan enhver sum af beføjelser på $\kvadratt{2}$ faktisk skrives i standardformularen $a\kvadratt{2}^2 + b\kvadratt{2} + c$. Nu, hvis du tilføjer, trækker eller multiplicerer to sådanne tal, så er det ikke svært at se, at vi får tal, som stadig kan sættes i standardformularen $a\kvm{2}^2 + b\kvm{2} + c$. Plus, hvad vi lige har vist her er, at den inverse af alle tal $a\kvm{2}^2 + b\kvm{2} + c$ kan også skrives i standardformular. Dette viser, at enhver tilføjelse, subtraktion, multiplikation og opdeling af tal i $\mathbb S{2}]$ giver et tal, som kan skrives i standardform… og dermed tilhører $\mathbb S{2}]$. I rene algebra termer er $ \ mathbb {2}]$ således stabil af de fire klassiske aritmetiske operationer. Af denne grund kalder vi det et felt.
geometri af Feltudvidelser
det felt, du er mest bekendt med, er sandsynligvis det sæt $\mathbb$ af rationelle tal. Andre eksempler på felter er sætene $\mathbb R$ af reelle tal og sæt $\mathbb C$ af komplekse tal. Og nu har vi også $\mathbb P{2}]$. Da $ \ mathbb S{2}]$ er et felt, der indeholder feltet $\mathbb S$, siger vi, at $\mathbb S{2}] / \mathb s$ er en feltudvidelse.
det faktum, at $\mathbb S{2}] / \mathbb S$ er en feltudvidelse, giver en meget naturlig forbindelse mellem de to felter. $\Mathbb S{2}]$ kan nemlig ses som et vektorrum, hvor $\mathbb S$ er det skalære felt. Især det faktum, at ethvert tal i $\mathbb S{2}]$ kan skrives $a \kvadrat s{2}^2 + b\kvadrat s{2} + c$ betyder, at $(1, \kvadrat s{2}, \kvadrat s{2}^2)$ danner et grundlag på $\mathbb S{2}]$ som et $\mathbb S$-vektorrum. Og det betyder, at vi kan repræsentere det geometrisk som et 3-dimensionelt rum!
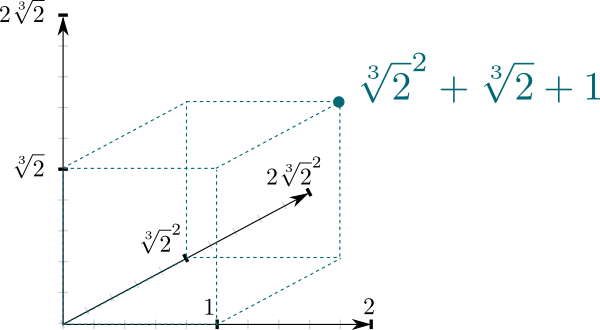
dimensionen af vektorrummet ovenfor er en interessant egenskab ved feltudvidelser. Det er kendt som graden, og det betegnes almindeligvis $\big{2}] : \mathbb S\big] = 3$ for eksempel.
Ja! Det er faktisk ret nemt at oprette en feltudvidelse af dette: bare tilføj nogle radikale tal, som ikke tilhører $\mathbb S{2}]$!
Ja! Dette ville skabe feltet $(\mathbb S{2}]) = \mathbb S{2},\kvm s{2}]$. Disse felter indeholder alle numre, der er produkter og beløb på $\kvm{2}$ og $\kvm{2}$. Disse er af formen $a $ $ {2}^2$ + $b \ $ {2} + c$ + $ d \ $ {2}^2 \ $ {2}$ + $ e \ $ {2} \ $ {2} $. Enhver ide om, hvad graden $ \ big{2}, \kvm{2}] : \mathbb S{2}]\big]$ er?
Ja! Faktisk har vi $a\$${2}^2$+$b\ $ {2} $ + $ c $ + $ d\ $ {2}^2\ $ {2} $ + $ e \${2} \${2} $ + $ f \ $ {2} $ = $ (a\ $ {2}^2+b\ $ {2}+c) $ + $ (d\ $ {2}}^2 + e \s{2} + F) \S S{2}$. Således kan et hvilket som helst antal $\mathbb{2},\kvm{2}]$ skrives $A+B\kvm{2}$, hvor $A$ og $B$ tilhører $\mathbb{2}]$. Således bestemmer 2 skalarer på $ \ mathbb med{2}]$ et tal i $ \ mathbb med{2}, \ kvm{2}]$. Dette betyder, at graden af feltudvidelsen $\mathbb S{2}, s{2}] / s{2}]$ er 2. Faktisk har vi Chasles-forholdet $ \ big{2}, \ kvm{2}]: \ mathbb S \ big] $ = $ \ big{2}, \ kvm{2}] : \mathbb S{2}] \ big] \ big{2}] : \mathbb S \big] $=$ 2 \gange 3 = 6$.
det er bedre end det! Enhver feltudvidelse af endelig grad, kaldet endelig feltudvidelse, er spændt af et enkelt tal. For eksempel $ \mathbb S{2}, $ \ mathbb S{2} + $ \mathbb S{2}]$, hvilket betyder, at alle tal, der er summen af beføjelser på$ \Kvadrat s{2} $og$ \kvadrat s{2}$, også er summen af beføjelser på$\Kvadrat s{2} + \kvadrat s{2}$. Er det ikke overraskende fantastisk?
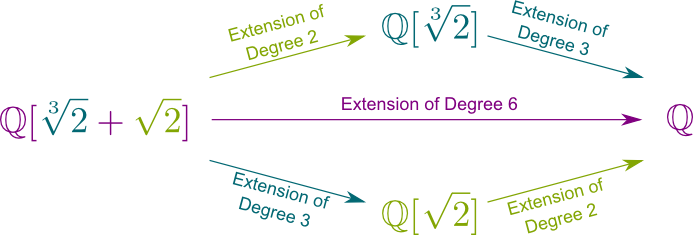
mere generelt kan enhver endelig feltudvidelse på $\mathbb$ skrives $\mathbb$ med nogle$$, som føjes til $\mathbb$.
Ja. Det er tilfældet for feltudvidelsen $ \ mathbb R / \ mathbb$. Og det er også den vigtigste feltudvidelse i Galois-teorien! Denne feltudvidelse er $ \ bar {\mathbb K} / \ mathbb K$, hvor $ \ bar {\mathbb K}$ er sættet med algebraiske tal. Disse er alle løsninger til polynomiske ligninger af formularen $a_n ^ n $ + $ a_{n-1} ^ {n-1} $+$ … $+$ a_1 $ + $ a_0 = 0$. For eksempel er $ {2}$ et algebraisk tal, fordi det er en løsning på $^4 – 2 gange = 0$. Således er $ \ bar {\mathbb S}$ en feltudvidelse til alle endelige feltudvidelser på $\mathbb S$.
Konjugatnumre
Vi er næsten der! Vi har brug for en endelig omvej gennem polynomiske ligninger.

præcis! Galois bemærkede, at nogle ligninger kunne forenkles. For eksempel kan $4-2 gange=0$ faktoriseres som $3-2=0$, hvilket svarer til $0$ eller $3-2=0$. Så ligningen $4-2 gange=0$ kan reduceres til ligninger $0$ og $3-2=0$. Og faktisk er denne reduktion meget lig, hvordan tal som 35 kan reduceres til 5 og 7, fordi $5 \gange 7 = 35$. Ligheden mellem ligninger og hele tal er så stærk, at vi endda kan lave euklidiske opdelinger af polynomer, ligesom du lærte at gøre det for tal! Til højre er et eksempel på en sådan opdeling (rolig, hvis du ikke forstår det, det vil ikke være vigtigt for efterfølgeren).
præcis! Disse er kendt som irreducible polynomiske ligninger. Ligningen $3-2 = 0$ er et eksempel på irreducerbar polynomligning.
Ja! Men afgørende, Galois ønskede at fokusere på ligninger med rationelle koefficienter. Eller rettere polynomer med koefficienter, der hører til basisfeltet. Så hvad jeg mente var, at for $\mathbb$ som basisfeltet er $3-2=0$ irreducible.
lad os overveje $2 – 2 gange -1=0$ for at have nogle spor. Denne ligning kan bevises at være irreducible. Kan du huske, hvordan du løser det?
Hvis $b^2 – 4ac \ gek 0$, Ja.
præcis! Så den irreducerbare polynomligning $2 + 2 gange -1=0$ har to løsninger: $1 + \ kvm{2}$ og $1 – \ kvm{2}$ … nogen kommentar?
Bingo! Det er den vigtigste opdagelse af Galois. Mere generelt kaldte Galois konjugater alle løsninger til en irreducible polynomligning. Og som du kan forestille dig, er disse vigtige for at fjerne radikaler fra nævnere!
den første ting at bemærke er, at hvis $1$, $2$,…, $$ $ $ er alle løsningerne af en polynomisk irreducible ligning $ a_n^n + a_{n-1}^{n-1}$ + $ … + a_1$ + a_0 = 0 $ med rationelle koefficienter, så kan denne polynomiske irreducible ligning faktisk omskrives $ a_n(1)(2)…(=0$. Identifikation af de konstante udtryk giver derefter $1 2 … $ $ = $ (-1)^n a_0/a_n$. Så afgørende er produktet af konjugerede tal det rationelle tal $(-1)^n a_0/a_n$, som ikke er nul (bevis det!).
Her er en lille vittighed for at huske den stærke forbindelse mellem konjugater:

overvej en brøkdel $1 / 1$, Hvor $1$ er et kompliceret udtryk med radikaler. Ved at multiplicere op og ned med konjugaterne $ 2$,…,$ $1$ $ 1 $ $ = $ (-1)^n a_n 2…$ 0$, som ikke har nogen radikal i nævneren, da vi har etableret$ a_0 $ for at være et ikke-nul nummer i basisfeltet!
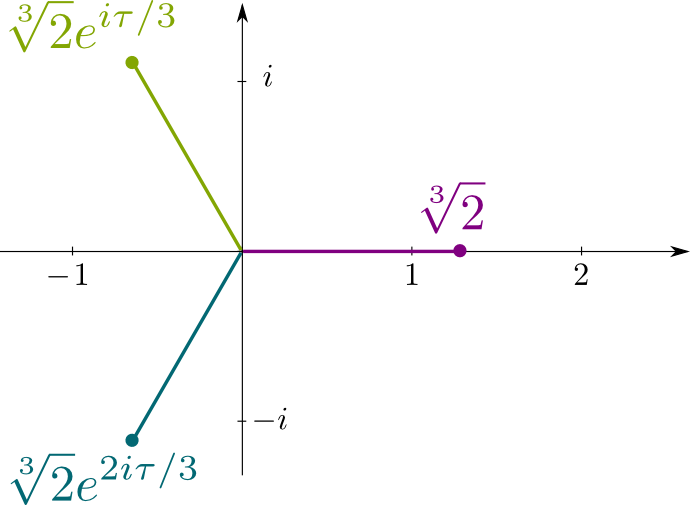
Husk at $3-2=0$ er den irreducerbare polynomligning $\kvm{2}$ er løsningen af. Så dens konjugater er de andre løsninger på den ligning, som er de komplekse tal $\kvm{2}j$ og $\kvm{2}j^2$, hvor $j= e^{i\tau/3}$ med $\tau = 2\pi$ er forholdet mellem omkredsen af en cirkel ved dens radius. Følgende figur viser placeringen af de konjugerede løsninger i dette komplekse plan:
Galois’ tvetydighed
endelig kommer vi til Galois nøgleindsigt!
konjugater er perfekt permutable. Dette betyder, at hvis du systematisk ændrer $\kvm{2}$ med dets konjugat $-\kvm{2}$, så holder lighederne stadig. For eksempel, da vi havde $1 / (\kvm{2}-1) = \kvm{2}+1$, Kan jeg ligefrem fortælle dig, at $1/(-\kvm{2}-1)=-\kvm{2}+1$! På samme måde har vi følgende fantastiske implikationer:
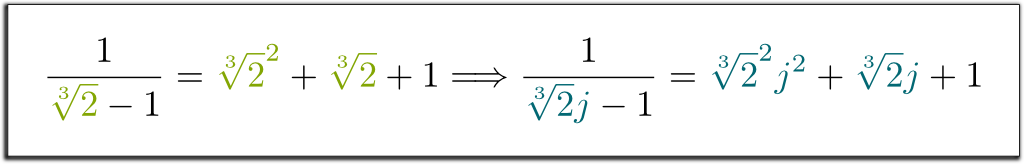
Hehe… Lad mig først huske, at endelige felter er spændt af et enkelt element. Så hvis basisfeltet er $ \ mathbb$, kan ethvert endeligt felt skrives $ \ mathbb $ $ for nogle rigtige $1$. Overvej nu $^n + a_{n-1}^{n-1} $+$ … + a_1 h + a_0 = 0$ den irreducerbare polynomligning $H_1$ er løsningen af. Hvad der derefter definerer $ \ mathbb $ er $ \ mathbb $ $ – vektorrummet spændt med $1$, $1^2$,…, $1^{n-1}$, med forenkling af større kræfter på $1$ i overensstemmelse med den algebraiske regel $1^n $=$ – a_{n-1}1^{n-1} $ – $ … – a_0$.
præcis! Afgørende er disse algebraiske regler for $ \ mathbb $ ikke rigtig afhængig af arten af $1$; de afhænger kun af det irreducible polynom $1$ er løsningen på! Derfor er reglerne for $\mathbb$ identiske med disse for $ \ mathbb$,…, $ \ mathbb$, hvor $1$ erstattes af en af dens konjugater $2$,…,$$$. Især fungerer felterne $ \ mathbb med{2}]$ og $\mathbb med{2} j]$ i overensstemmelse med de nøjagtige samme regler. Derfor er konjugater perfekt permutable! Vi siger, at felterne $ \ mathbb S{2}]$ og $ \ mathbb S{2} j]$ er isomorfe, og at erstatning af $\kvadrat s{2}$ med $\kvadrat s{2}j$ er en isomorfisme $\mathbb S{2}] \højre pil \mathb S{2}j]$.
på en meget lignende (men stærkere) måde, at to vektorrum af dimension 2 er mere eller mindre ens! Dette har en frygtelig konsekvens. Det betyder, at det fra et algebraisk perspektiv er meningsløst at gøre en forskel mellem et tal og et hvilket som helst af dets konjugater (så længe du systematisk erstatter nummeret med dets konjugat)! Så for eksempel er$ \${2}$ og $ – \ $ {2} $ algebraisk uadskillelige! For at huske dette, her er en anden vittighed, jeg er kommet med:

slet ikke! Enhver skelnen mellem disse to tal skal involvere en anden matematik end algebra, som ordrerelationer eller topologi. Hvad jeg mener er, at for eksempel forholdet $\kvm{2} > 0$ gør en forskel mellem $\kvm{2}$ med $-\kvm{2}$, men det er fordi det involverer en ordrerelation. Men hvis vi begrænser os til polynomiske ligheder, så er der absolut ingen forskel mellem $\kvm{2}$ og $-\kvm{2}$. På samme måde er $i$ og $-i$, løsningerne af den irreducerbare polynomligning $2+1=0$, også algebraisk uadskillelige. Alligevel kalder vi vilkårligt $i$ en af dem. Derfor kaldte Galois sin teori teorien om tvetydighed. I dag kaldes tvetydigheden ved valget af den konventionelle kvadratrod på $-1$ blandt $i$ og $-i$ snarere symmetrien mellem $I$ og $-i$.
Galois-grupper
Galois fokuserede især på feltudvidelser, der er stabile ved konjugation. Sådanne stabile feltudvidelser er nu kendt som Galois-udvidelser. Så hvis $1$ tilhører en Galois-udvidelse, indeholder denne Galois-udvidelse alle dens konjugater $2$,…,$$$.
en enkel måde at konstruere Galois-udvidelser på består i at tage feltet spændt af løsninger af en irreducerbar polynomligning. For eksempel, hvis $1$,…, $$ $er konjugater for basisfeltet$ \mathbb$$, så er $ \mathbb $ / \mathbb $ en Galois-udvidelse. Felter konstrueret på denne måde kaldes opdelingsfelter.
for eksempel er opdelingsfeltet i ligningen $^3-2=0$ Galois-udvidelsen $\mathbb S{2}, \kvadrat{2} j, \kvadrat{2} j^2] / \mathbb S$ spændt af dets løsninger.
Hvis $1$ spænder over en Galois-udvidelse, så gør dens konjugater det også. Således $ \ mathbb S = \ mathbb S = $ … $= \ mathbb S$ = $ \ mathbb S$. Således er isomorfismen mellem $ \ mathbb $ og $ \ mathbb$, som består i altid at erstatte $1$ med $2$, faktisk en isomorfisme mellem $\mathbb$ og sig selv! Vi kalder det en automorfisme. En Galois-udvidelse$\mathbb K/ \ mathbb k $ danner Galois-gruppen $ Gal (\mathbb K/ \ mathbb K)$.
nu, afgørende, hvis $\mathbb S = \mathbb S$, så er alle automorfier af en Galois-udvidelse $\mathbb S/ \mathbb S$ permutationer af $s_1$ med en af dens konjugater! Især ser vi her, at kardinaliteten af en Galois-gruppe svarer til graden af Galois-udvidelsen.
sikker! Du kan bemærke, at $ \ mathbb S = \ mathbb S$ og $ \ mathb s$, hvilket betyder, at $i$ og $S{2}$ hver spænder over opdelingsfelterne i den irreducerbare polynomligning, de er løsning af. Således er $\mathbb$/\mathbb $og$ \mathbb $ /\mathbb $ begge Galois-udvidelser. Derfor består deres automorfier i at erstatte $i$ med et af dets konjugater, $i$ eller $-i$, og erstatte $\$ {2} $med$ \${2}$eller $ – \ $ {2}$. I de første tilfælde ændrer vi ikke noget til tal, hvilket svarer til nulsymmetrien. De andet tilfælde kan visualiseres som aksiale symmetrier, som vist i nedenstående figur:

er det ikke fantastisk?
sikker! Lad os komme til opdelingsfeltet $\mathbb med{2},\kvm{2}j, \kvm{2}j^2]$ på $3-2=0$. Men før vi går videre, lad os bemærke, at $\mathbb S{2},\kvm s{2}j, \kvm s{2}j^2] = \mathbb S{2}, j]$.
alt vi behøver at bevise er, at alle generatorer af et felt tilhører den anden. Lad os starte med at bevise, at generatorerne af sidstnævnte, $\$ {2} $og$ j$, tilhører førstnævnte. Det er indlysende for $ $ {2}$. Nu, $j = (\kvm{2} j) / \ kvm{2}$, således $j$ hører også til det tidligere felt. Dette beviser, at alle elementer i $\mathbb S{2},j]$ tilhører $\mathbb S{2}, \kvm s{2} j, \kvm s{2} j^2]$. Gensidigt er det ligetil, at alle generatorer af det tidligere felt, $ \ kvm{2}$, $ \ kvm{2}j$ og $\kvm{2}j^2$, er produkter fra generatorerne af sidstnævnte. Således er begge felter ens. Og især $ \ mathbb S{2}, j]/ \ mathbb S$ er en Galois-udvidelse.
Hehe…for at forstå symmetrierne i $\mathbb{2}]$, bliver vi nødt til at gå videre i Galois’ undersøgelse af Galois-grupper …
Galois korrespondance
problemet med Galois-grupper er, at de kan blive ekstremt store og komplicerede. Dette er især tilfældet med den uendelige gruppe $Gal (\bar {\mathbb S}/ \ mathbb S)$. For at pågribe sådanne store og komplekse grupper havde Galois den strålende ide at bryde disse i mindre stykker.
Jeg ved det! Jeg kan godt lide at visualisere disse symmetrier som måder at tilslutte $\mathbb S{2},j]$ til $\mathbb S$. Her er et afbildet billede af “plugging onto”:
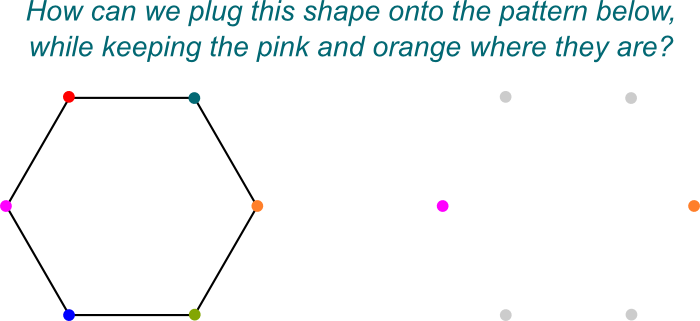
præcis! Og det er simpelthen fordi $ \ mathbb S{2}, j]$ er en Galois-udvidelse af $\mathbb S$, som i sig selv er en feltudvidelse på $\mathbb S$.
og der er mere! Galois viste, at alle undergrupper af en Galois udvidelser opnås på denne måde! Mere præcist er kortlægningen af ethvert felt $k$ imellem Galois-udvidelsen $ \ mathbb S{2}, j]$ og basisfeltet $\mathbb S$ til Galois-gruppen $Gal(\mathbb S{2},j] / K)$ bijektiv. Denne kendsgerning kaldes Galois korrespondance! Denne korrespondance vises skematisk nedenfor for en Galois-udvidelse $\mathbb S/\mathbb S$.

i stedet for at forsøge at beskrive denne gruppe direkte, lad os fokusere på dens undergruppe $Gal(\mathbb S{2}, j]/\mathbb S)$. Det er ligetil, at $ \ kvm{2} $ spænder over $ \ mathbb med{2}, j]$, når det føjes til $ \ mathbb med$. Således er $ \ mathbb S{2}, j] / \mathbb S$ en Galois-udvidelse, der spænder over $ \ S{2}$. Derfor ved vi ved hjælp af en sætning, Vi har set tidligere, at alle automorfier i denne Galois-udvidelse består i at erstatte $\kvm{2}$ med et af dets 3 konjugater (i sig selv $\kvm{2} j$ og $\kvm{2} j^2$)!
nu kunne jeg fortsætte med at studere andre stykker af $Gal(\mathbb K{2}, j]/\mathbb K)$, ligesom Galois-undergruppen $Gal(\mathbb K{2},j]/\mathbb K{2}])$. Men jeg vil hellere bruge en anden af Galois ‘ magtfulde sætninger. Han beviste nemlig, at hvis $\mathbb S/\mathbb S$ desuden var en Galois-udvidelse i sig selv, så er undergruppen $Gal(\mathbb S{2}, j]/\mathbb S)$ normal.
således kan Galois-gruppen på $\mathbb med{2}, j]/\mathbb$ kvotienteres af denne undergruppe,og kvotientgruppen er Derefter lig med $Gal(\mathbb med / \mathbb med)$. Alligevel er $ \ mathbb $ / \ mathbb$ faktisk en Galois-udvidelse spændt af $j$, hvis konjugat er $j^2$. $Gal (\mathbb S/ \ mathbb S)$ består således i enten at forlade $j$ som $j$ eller erstatte den med $j^2$.
Vi kan nu udlede alle symmetrier på $ Gal (\mathbb K{2},j]/\mathbb k)$ ved at kombinere disse på $Gal (\mathbb K{2},j] / \mathbb K)$ og $Gal (\mathbb K/ \ mathbb K)$. Vi kan vise disse symmetrier ved at tegne, hvordan de påvirker vores tre spændende konjugater $\KVRT{2}$, $\KVRT{2}j$ og $\KVRT{2}j^2$:
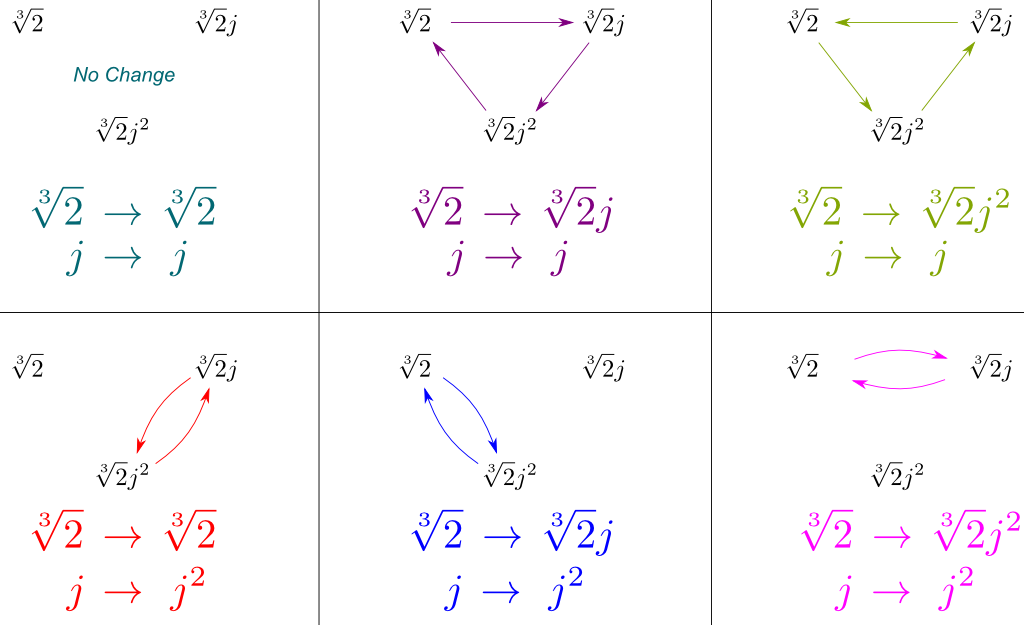
afgørende indeholder figuren ovenfor alle symmetrier af $Gal(\mathbb K{2}, j] / \mathbb K)$. Og forbløffende svarer disse symmetrier til den velkendte gruppe af symmetri.
Jeg vil lade Marcus du Sautoy præsentere det for dig:
så er symmetrier her som en søstjerne eller som en trekant?
ja, ja! Denne gruppe af symmetrier i trekanten kaldes $D_3$, og den er den samme som gruppen $S_3$ af permutationer af 3 elementer. Dette fører os til følgende formel, som jeg fandt så smuk, at jeg har besluttet at indramme det!
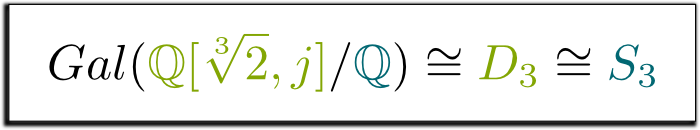
lad os konkludere
på mange måder skal Galois betragtes som far til moderne algebra. Hans vigtigste indsigt var at se på matematik gennem vinklen på operationsreglerne, og dette førte ham til at afsløre overraskende og indsigtsfulde uklarheder eller symmetrier mellem tal. Fra et algebraisk perspektiv er tal som $ $ {2}$, $ $ {2}j$ og $ $ {2}j^2$ faktisk perfekt symmetriske og fuldstændig udskiftelige.
forståelsen af disse symmetrier har haft forbløffende anvendelser i algebraisk geometri og algebraisk topologi blandt andre. Især tidlige succeser af teorien inkluderer en klassificering af konstruerbare regelmæssige polygoner og en sætning, der hævder, at høj grad polynomiske ligninger ikke kunne løses af radikaler.
nylige succeser vises i kryptografi og Andrey viles’ bevis for Fermats sidste sætning. Dette bevis indebærer at studere Galois group $ Gal (\bar {\mathbb K} / \ mathbb K)$ med grupperepræsentation. Men jeg vil sige, at teorien på en eller anden måde stadig er ung, og der er meget tilbage at opdage. Det er trods alt et af de mest aktive forskningsområder i nutidens rene matematikforskning.
dette skulle få os til at betale mange flere hyldest til Galois’ utrolige geni… Lad mig inkludere en af SocraticaStudios.