en integreret del af væskedynamikken er vorticitet. Heuristisk måler den den lokale rotation af en væskepakke. For faste genstande taler vi ikke om et objekts vorticitet, men i stedet henviser vi til dets vinkelhastighed. Disse to begreber er relaterede, men vorticitet er mere nyttigt, når man diskuterer roterende objekter, der deformeres, som en væske gør.

vorticiteten af et givet hastighedsfelt inden for et givet plan beregnes ved at vælge to ortogonale akser i dette plan og tilføje vinkelhastigheden for hver akse. I en fast genstand eller en væske, der roterer som en fast genstand (passende navngivet fast kropsrotation), er vorticiteten dobbelt så meget vinkelhastighed, da hver akse roterer med samme hastighed. Men i en væske kan de to akser rotere med meget forskellige hastigheder og endda forskellige retninger! Det er endda muligt, at hver akse kan rotere, men netto vorticitet er nul (se irrotational hvirvel).

hvis bevægelsen af en væske er strengt begrænset til at ligge i et plan, tages vorticitetsvektoren til at være ortogonal i forhold til planet og kan ikke ændre retninger (eller vippe). Det eneste aspekt af vorticiteten, der kan ændre sig, er dens størrelse. Det antages, at denne overførsel af energi til større skalaer er forbundet med dannelsen af den store røde plet på Jupiter.

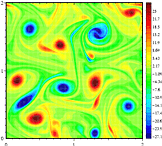
i tredimensionel væskebevægelse er vorticitetsvektoren tredimensionel, idet den har komponenter parallelt med hver akse, H, y og å: h-komponenten er parallel med å-aksen og beskriver rotationshastigheden i h-planet. Det er på grund af denne dikotomi, at der er en kvalitativ forskel i adfærd mellem todimensionel turbulens og tredimensionel turbulens. I førstnævnte er der en tendens til, at hvirvler klumper sig sammen og danner større hvirvler, hvorimod i sidstnævnte Rives De vortiske bevægelser fra hinanden, og energien kaskader ned til de mindste skalaer, hvor den derefter diffunderes væk.

matematisk er vorticiteten af et givet hastighedsfelt

er defineret til at være hastighedsfeltets krølle og betegnes normalt med det græske bogstav omega,

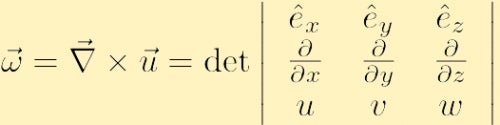
hvor vi har brugt det konventionelle nabla-symbol til gradienten:

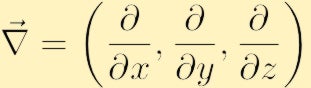
i komponentform findes vorticiteten ved at udvide determinanten ovenfor,

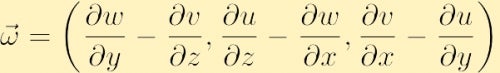
et andet vigtigt aspekt af væskedynamik, der er relateret til vorticitet, er cirkulation. I modsætning til vorticitet, som er en lokal ejendom, defineret på hvert punkt i rummet, er cirkulation en global ejendom, defineret ved at integrere en egenskab af væsken over en kurve. Især hvis du vælger en lukket kontur og betegner den med bogstavet C(t), er cirkulationen omkring C(t) i retning mod uret en skalar mængde betegnet med,

er defineret som

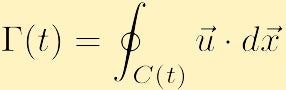
hvilket er kan være en funktion af tiden, ligesom den lukkede kontur.

lad os tage et øjeblik til at forklare, hvad dette siger fysisk. På hvert punkt på contourC(t) finder vi komponenten af hastigheden, der er tangent til kurven og multiplicerer denne skalar med en uendelig længde; projicering af hastigheden på tangenten vil nødvendigvis give en størrelse mellem hastigheden i den position og nul. Hvis hastigheden er tangent til kurven, får vi plus eller minus hastigheden på , hvis hastigheden er vinkelret på kurven, får vi nul. Derefter integrerer vi denne mængde, en anden måde at sige opsummering af et uendeligt antal ting omkring konturen, så vi tilføjer bidraget fra hvert punkt. Herfra konstaterer vi, at cirkulationen langs en kontur C (t) er mængden af strømning omkring contourC (t); et positivt eller negativt resultat svarer til henholdsvis kontur med uret eller med uret. Et ekstremt tilfælde er, hvor hastighedsfeltet er overalt vinkelret på kurven C(t), og derfor er der ingen cirkulation, da strømmen altid krydser konturen og aldrig strømmer langs konturen. For at få en ikke-nul cirkulation skal der være en del af kurven, hvor strømmen er langs den lukkede kontur.

hvis hastighedsfeltet er glat, og der ikke er nogen singulariteter inden for C(t), kan vi bruge Stokes’ integrerede sætning fra vektorberegning til at omskrive cirkulationen som,

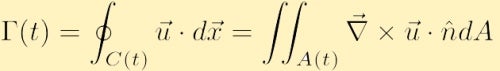
hvor A er det område, der er indeholdt i konturen C, og kur er enhedens normale vektor til areaA.

før vi overvejer denne nye ligning for cirkulationen, er det nyttigt at forstå den fysiske betydning for Stokes’ sætning, hvor vektorfeltet er hastigheden. I dobbeltintegralet ovenfor beregner vi vorticiteten på hvert punkt i konturen og opsummerer derefter vorticiteten over alle disse punkter i a(t). I det enkelte integral over den lukkede kontur beregner vi strømmen langs områdets grænse. Stokes ‘ sætning siger derefter, at disse mængder er ens, og således at hvis der er gennemsnitlig vorticitet inden for et område, som derefter skal betyde, at området har en ikke-nul rotationshastighed, skal der derfor være en nettocirkulation langs omkredsen af denne grænse.

fra den gennemsnitlige værdi sætning af calculus kan vi erstatte integranden i dobbeltintegralet med en middelværdi, der svarer til den gennemsnitlige komponent af vorticiteten ortogonal til det plan, hvori C(t) ligger. Således er den anden fortolkning af cirkulation, at det er den gennemsnitlige vorticitet gange området indeholdt i C(t). I stedet for at beregne cirkulationen på den lukkede kontur C(t) kan vi beregne den gennemsnitlige vorticitet normal til A (t) og multiplicere den med området indeni. Hvis du overvejer det specielle tilfælde, hvor vorticiteten er overalt konstant, ville cirkulationen være størrelsen af vorticitetstider det område, der er indeholdt i.

en punktvirvel er en hvirvel, der ikke har noget område, hvilket betyder, at vorticitet kun er til stede på et enkelt punkt. For at studere punkthvirvler antager vi først, at vi har en 2D ukomprimerbar strømning. (Punkthvirvler kaldes også undertiden linjehvirvler, når de ses i 3D.)

efter nogle beregninger bestemmer vi, at hastighedsfeltet, der genereres af en punktvirvel, i kompleks form, som er placeret ved S0, er givet af (hvor Gamma nul er cirkulationen omkring punktvirvel, som ofte omtales som styrken af punktvirvel):

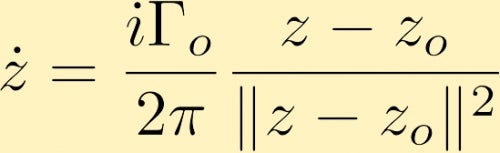
hastighedsfeltet, der genereres af en punktvirvel, kan få et andet punktvirvel til at Flyt dig. Her er et par eksempler på dette: De to punkts hvirvler, både positive og af samme størrelse, de to punkts hvirvler, begge positive, men den ene har tredobbelt styrken af den anden, og den ene punkts hvirvel er negativ med dobbelt så stor som den anden, som er positiv . En anden mulighed er at overveje to punkthvirvler af samme størrelse, men modsat tegn.

dette kan udvides til et hvilket som helst antal punkthvirvler, N. bevægelsesligningen i kompleks form for en punktvirvel alfa er givet ved:

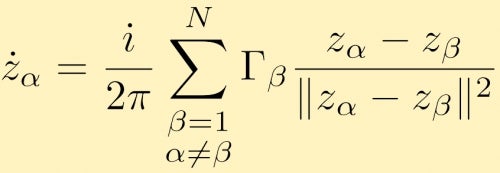
at se på interaktionerne mellem punkthvirvler er et meget interessant problem, som er vanskeligt at gøre analytisk, især da antallet af punkthvirvler stiger. Numeriske simuleringer af punktvirvel-interaktioner er således meget almindelige. En nyttig anvendelse af store punkt hvirvel simuleringer er, hvis man ser på store klynger af punkt hvirvler, der simulerer hvirvler med begrænset område. Her er beskrivelser og resultaterne af flere store punkt hvirvel simuleringer. I dette tilfælde har vi to store klynger af punkthvirvler med samme styrke, der smelter sammen. I det næste tilfælde starter vi med en ring af grupperede punkt veracities.

for at finde en ligning for udviklingen af vorticiteten begynder vi med momentumligningen. I momentumligningen kan det advektive udtryk omskrives som følger,

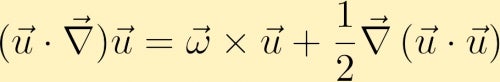
Vi beregner derefter krøllet i momentumligningen, og gennem nogle vektoridentiteter får vi vorticitetsligningen:

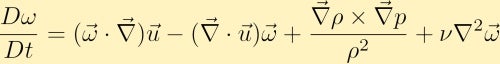
vorticitetsligningen viser, hvordan vorticitet kan genereres i en væske. Uden tab af generalitet antager vi, at vi oprindeligt kun har vorticitet i å-retning. Herfra kan vi se, hvordan hvert af de fire forskellige udtryk kan ændre vorticiteten.

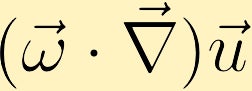
Hvis der er en ændring i hastighed med retning af eksisterende vorticitet, kan vorticitet genereres.

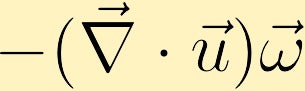
hvis en væskepakke ekspanderer, og vorticiteten er positiv, vil vorticiteten af væskepakken falde, og hvis pakken kontraherer, vil vorticiteten stige.

væskelag med konstant densitet (isopyknaler) ønsker at falde sammen med lag med konstant tryk (isobarer). Hvis disse lag ikke falder sammen, begynder væsken at rotere for at få dem til at lineere op, hvilket får vorticitet til at blive genereret. (I eksemplet starter vi med nul vorticitet.)

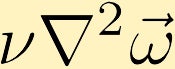
viskøse kræfter forårsager diffusion af vorticitet. (I eksemplet starter vi med et punkt med uendelig vorticitet i midten.)