Die revolutionäre Galois-Theorie

Am 31.Mai 1832 starb ein französischer republikanischer Revolutionär namens Évariste Galois an einem Schuss. Er war 20 Jahre alt. In der Nacht zuvor hatte Galois aus Angst vor seinem eigenen Tod viele Briefe geschrieben und frenetisch gekritzelt: „Ich habe keine Zeit; Ich habe keine Zeit“. Ein Brief ist aus historischen Gründen besonders wertvoll. In diesem Brief behauptet Galois, die Revolution tatsächlich ausgelöst zu haben. Keine politische. Aber eine mathematische.
Die Revolution, die Galois initiierte, erwies sich als größer und tiefgreifender, als er es sich hätte vorstellen können! Die Landschaft der Mathematik wurde tief von Galois‘ Vision betroffen, wie seine Nachkommen gestiegen ist und die mathematische Welt übernommen. Diese Nachkommenschaft ist jetzt allgegenwärtig und regiert grenzenlose Länder. Es geht unter dem Namen reine Algebra.
Um das Erzählen von Galois ‚dramatischem Leben noch ein bisschen mehr zu romantisieren, hier eine Zusammenfassung eines Dokumentarfilms, den ich über Algebra gemacht habe:

Das ist er definitiv! Aber seine mathematische Revolution verlief nicht reibungslos. Wie alle Revolutionsführer hatte er zunächst die größten Schwierigkeiten. Die Revolution nicht vorstellen. Aber um andere davon zu überzeugen, sich ihm in einem bahnbrechenden Ansatz zur Mathematik anzuschließen. Als Galois noch lebte, wurden seine revolutionären Ideen mehrmals von der französischen Akademie der Wissenschaften abgelehnt … Weil die besten französischen Mathematiker dieser Zeit wie Siméon Denis Poisson es einfach nicht bekommen konnten! Teilweise wegen Galois ‚unleserlicher Handschrift auf der rechten Seite …
Es war definitiv ein großer Schub. Aber es würde weitere 82 Jahre dauern, bis der große österreichische Mathematiker Emil Artin der Galois-Theorie 1942 endlich ihre moderne Form gab. Artin verdient viele Credits. Während Galois der Visionär war, der diese Revolution vorausgesehen hat, ist Artin in vielerlei Hinsicht derjenige, der die Revolution tatsächlich unternommen und die Mathematik umgeworfen hat. Dank Artin und einigen anderen ist die Galois-Theorie heute zu einem unvermeidlichen Eckpfeiler der mathematischen Forschung geworden, mit vielen überraschenden und erstaunlichen Errungenschaften (wie Wiles ‚Beweis für Fermats letzten Satz) sowie einem riesigen Reservoir an offenen Fragen und Mysterien!
Felder in der reinen Algebra
In der Galois-Theorie geht es um Symmetrien von Zahlen. Aber bevor ich dorthin komme, muss ich Ihnen vorstellen, wie Sie sich bewaffnen können, indem ich Sie über ein Geheimnis über Zahlen informiere. Und ich bin sicher, Sie haben davon gehört! Tatsächlich, zurück in der High School, Sie wurden wahrscheinlich nie gelehrt Wurzeln in den Nennern zu verlassen.
Ich meine, dass $ 1/(\sqrt{2} -1) $ keine richtige Antwort war. Können Sie helfen, die Quadratwurzel von 2 im Nenner loszuwerden?
Hehe … Uns wurde beigebracht, mit dem Konjugat des Nenners auf und ab zu multiplizieren. Dieses Konjugat wird erhalten, indem $-$ durch $+$ (oder umgekehrt) im Nenner ersetzt wird:
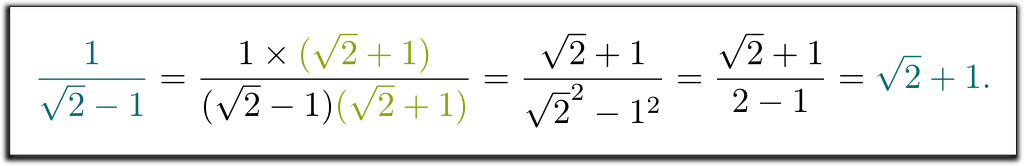
Ich weiß! Der komplizierte Ausdruck $1/(\sqrt{2}-1)$ repräsentiert dieselbe Zahl wie $\sqrt{2}+1$. Und das erklärt, warum unsere Lehrer wollten, dass wir die Ergebnisse eher auf die eine als auf die andere Weise schreiben: Wenn alles auf die gleiche Weise geschrieben wird, werden Prüfungen viel einfacher zu korrigieren!
Aber was ist mit $1/(\sqrt{2}-1)$? Kannst du die Wurzel im Nenner loswerden? Kann es überhaupt gemacht werden?
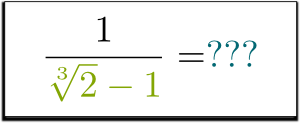
Ich weiß!
Du sagst es mir!
Glück gehabt?
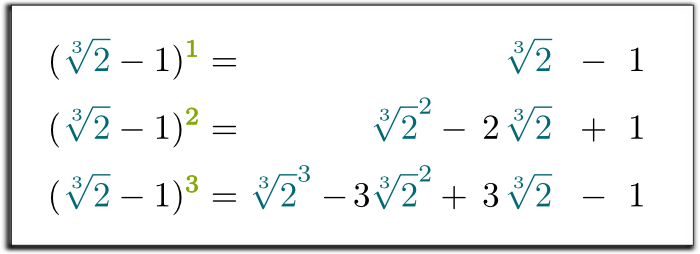
Ja, das ist es! Durch diese Substitution in der dritten Gleichung haben wir gezeigt, dass die drei ersten Potenzen von $ \ sqrt {2} -1 $ als Summe einer rationalen Zahl geschrieben werden können, von $ \ sqrt {2} $ und von $ \ sqrt {2} ^ 2 $!
Wir haben also jetzt 3 Gleichungen mit 2 Wurzelausdrücken, die wir loswerden wollen! So können wir die Gleichungen kombinieren, um alle Wurzelausdrücke auf der rechten Seite zu entfernen!
Multiplizieren wir die 2 ersten Zeilen mit 3 und addieren alle 3 Gleichungen:
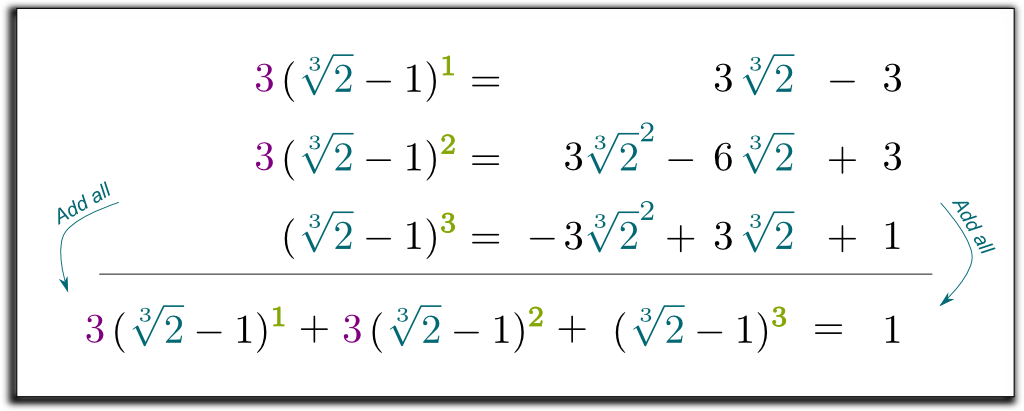
Hehe … Das Coole ist, dass der linke Term, den wir erhalten haben, jetzt durch $\sqrt{2} -1 $ faktorisiert werden kann! Lassen Sie mich einige langweilige Berechnungen überspringen … Und zum Ergebnis kommen $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Um also die Wurzeln im Nenner loszuwerden, können wir mit $ \sqrt{2} ^ 2 + \sqrt{2} + 1 $ auf und ab multiplizieren! Schließlich erhalten wir die folgende überraschende und schöne Formel:
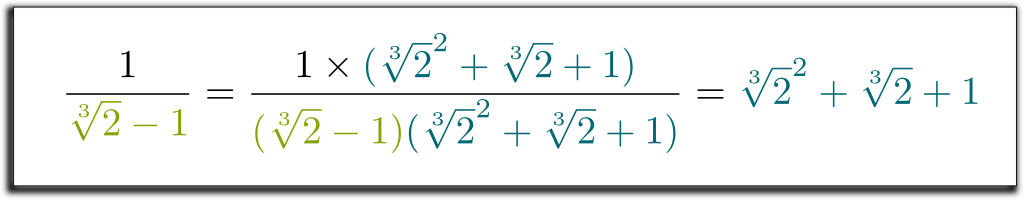
Ich weiß! Aber was noch schöner ist, ist, dass die Methode, die wir verwendet haben, sehr allgemein ist! Mit ähnlichen Techniken können wir jetzt alle Radikale aus dem Nenner entfernen!
Was für Galois von besonderem Interesse war, war nicht die Tatsache, dass eine Methode es ermöglichte, Radikale aus Nennern zu entfernen. Vielmehr entsprach jede Zahl mit Radikalen im Nenner einer Zahl mit Radikalen oben. Dies bedeutete, dass die Zahlen mit Radikalen oben durch Division stabil waren.
Es ist üblich, $\math [ Q{2}]$ die Menge von Zahlen zu bezeichnen, die als Summe von Potenzen von $\sqrt{2}$ geschrieben werden kann. Da $ \sqrt{2} ^ 3 = 2 $ eine rationale Zahl ist, kann jede Summe von Potenzen von $ \sqrt{2} $ tatsächlich in der Standardform $ a \sqrt{2}^ 2 + b \ sqrt{2} + c $ geschrieben werden. Wenn Sie nun zwei solche Zahlen addieren, subtrahieren oder multiplizieren, ist es nicht schwer zu erkennen, dass wir Zahlen erhalten, die immer noch in der Standardform $a\sqrt{2}^2 + b\sqrt{2} + c$ . Außerdem haben wir hier gerade gezeigt, dass die Umkehrung aller Zahlen $ a \ sqrt {2} ^ 2 + b \ sqrt {2} + c $ auch in Standardform geschrieben werden kann. Dies zeigt, dass jede Addition, Subtraktion, Multiplikation und Division von Zahlen in $ \mathbb Q{2}] $ eine Zahl ergibt, die in Standardform geschrieben werden kann … und somit zu $\mathbb Q{2}] $ gehört. In reiner Algebra ist $ \ mathbb Q{2}] $ also durch die vier klassischen arithmetischen Operationen stabil. Aus diesem Grund nennen wir es ein Feld.
Geometrie von Felderweiterungen
Das Feld, mit dem Sie am meisten vertraut sind, ist wahrscheinlich die Menge $\mathbb Q$ rationaler Zahlen. Andere Beispiele für Felder sind die Mengen $ \ mathbb R $ reeller Zahlen und die Menge $\ mathbb C $ komplexer Zahlen. Und jetzt haben wir auch $\math [ Q{2}]$ . Da $\mathbb Q{2}]$ ein Feld ist, das das Feld $\mathbb Q$ enthält, sagen wir, dass $\mathbb Q{2}] / \mathbb Q$ eine Felderweiterung ist.Tatsächlich kann gezeigt werden, dass, wenn ein Feld $k$ $ x +x + \ldots+x \neq 0$ für alle endlichen Summen und alle $ x \neq 0$ erfüllt, $k $ $\mathbb Q $ enthalten muss. Andernfalls wird das Feld $ k $ notwendigerweise auf endlichen Feldern $ \ mathbb Z / p \ mathbb Z $ , auch bekannt als $ \ mathbb F_p $, aufgebaut, wobei $ p $ Primzahl ist. In diesen Feldern ist eine Summe von $ p $ -Elementen $x $ immer gleich 0. Tatsächlich sind alle endlichen Felder $ \ mathbb F_ {p ^ n} \ cong \ mathbb F_p ^ n $ wobei $ n $ eine ganze Zahl und $ p $ eine Primzahl ist. Diese endlichen Felder sind in der Informatik und Kryptographie unerlässlich!
Die Tatsache, dass $\mathbb Q{2}] / \mathbb Q$ eine Felderweiterung ist, ergibt eine sehr natürliche Verbindung zwischen den beiden Feldern. $ \mathbb Q{2}] $ kann nämlich als Vektorraum gesehen werden, wobei $ \ mathbb Q $ das skalare Feld ist. Insbesondere die Tatsache, dass eine beliebige Zahl in $\mathbb Q{2}] $ geschrieben werden kann $a \sqrt{2} ^2 + b\sqrt{2} + c $ bedeutet, dass $(1, \sqrt{2}, \sqrt{2} ^2) $ eine Basis von $ \mathbb Q{2}] $ als $ \ mathbb Q $ -Vektorraum bildet. Und das bedeutet, dass wir es geometrisch als 3-dimensionalen Raum darstellen können!
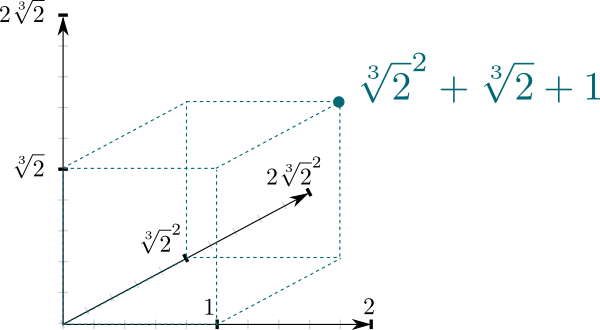
Die Dimension des obigen Vektorraums ist eine interessante Eigenschaft von Felderweiterungen. Es ist als Grad bekannt und wird allgemein als $ \ big{2}] bezeichnet: \ math [ Q \big] = 3 $ zum Beispiel.
Ja! Es ist eigentlich ziemlich einfach, eine Felderweiterung davon zu erstellen: Fügen Sie einfach eine radikale Zahl hinzu, die nicht zu $\mathbb Q{2}] $ gehört!
Ja! Dies würde das Feld $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$ . Diese Felder enthalten alle Zahlen, die Produkte und Summen von $\sqrt{2}$ und $\sqrt{2} $ sind. Diese haben die Form $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. Irgendeine Vorstellung davon, was der Grad $\big{2}, \sqrt{2}] : \math [ Q{2}]\big] $ ist?
Ja! In der Tat haben wir $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e \sqrt{2} + f) \sqrt{2}$. Somit kann eine beliebige Anzahl von $\mathbb Q{2},\sqrt{2}]$ $A+B\sqrt{2}$ geschrieben werden, wobei $A$ und $B$ zu $ \mathbb Q{2}] $ gehören. Somit bestimmen 2 Skalare von $\mathbb Q{2}]$ eine Zahl in $\mathbb Q{2},\sqrt{2}]$ . Dies bedeutet, dass der Grad der Felderweiterung $\mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ 2 ist. Tatsächlich haben wir die Chasles-Relation $\big{2}, \sqrt{2}] : \math [ Q \big] $=$ \big{2}, \sqrt{2}] : \mathbb Q{2}] \groß] \groß{2}] : \mathbb Q \groß] $ = $ 2 \ mal 3 = 6 $.
Es ist besser als das! Jede Felderweiterung endlichen Grades, die als endliche Felderweiterung bezeichnet wird, wird von einer einzelnen Zahl überspannt. Zum Beispiel $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$ , was bedeutet, dass alle Zahlen, die Summen von Potenzen von $\sqrt{2} $ und $ \sqrt{2}$ sind, auch Summen von Potenzen von $ \sqrt{2} + \sqrt{2} $ sind. Ist es nicht überraschend genial?
Allgemeiner kann jede endliche Felderweiterung von $\mathbb Q$ mit $x$ geschrieben werden, das zu $\mathbb Q $ hinzugefügt wird.
Ja. Dies ist der Fall für die Felderweiterung $\mathbb R/\mathbb Q$ . Und, so ist die wichtigste Felderweiterung in der Galois-Theorie! Diese Felderweiterung ist $ \bar{\mathbb Q} /\mathbb Q$, wobei $\bar{\mathbb Q} $ die Menge der algebraischen Zahlen ist. Dies sind alles Lösungen für Polynomgleichungen der Form $a_n x ^ n $+$ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $+$ a_0 = 0$. Zum Beispiel ist $ \sqrt{2} $ eine algebraische Zahl, weil sie Lösung zu $ x ^ 4 – 2x = 0 $ ist. Somit ist $\bar{\mathbb Q}$ eine Felderweiterung für alle endlichen Felderweiterungen von $\mathbb Q$.
Konjugierte Zahlen
Wir sind fast da! Wir brauchen einen letzten Umweg durch Polynomgleichungen.

Genau! Galois bemerkte, dass einige Gleichungen vereinfacht werden könnten. Zum Beispiel kann $ x ^ 4-2x = 0 $ als $ x (x ^ 3-2) = 0 $ faktorisiert werden, was $ x = 0 $ oder $ x ^ 3-2 = 0 $ entspricht. Die Gleichung $ x ^ 4-2x = 0 $ kann also auf die Gleichungen $ x = 0 $ und $ x ^ 3-2 = 0 $ reduziert werden. Und in der Tat ist diese Reduktion sehr ähnlich, wie Zahlen wie 35 auf 5 und 7 reduziert werden können, weil $ 5 \ mal 7 = 35 $. Die Ähnlichkeit zwischen Gleichungen und ganzen Zahlen ist so stark, dass wir sogar euklidische Divisionen von Polynomen machen können, genau wie Sie es für Zahlen gelernt haben! Rechts ist ein Beispiel für eine solche Aufteilung (keine Sorge, wenn Sie es nicht verstehen, wird es für die Fortsetzung nicht wichtig sein).
Genau! Diese werden als irreduzible Polynomgleichungen bezeichnet. Die Gleichung $ x ^ 3-2 = 0 $ ist ein Beispiel für irreduzible Polynomgleichungen.
Ja! Entscheidend war jedoch, dass Galois sich auf Gleichungen mit rationalen Koeffizienten konzentrieren wollte. Oder vielmehr Polynome mit Koeffizienten, die zum Basisfeld gehören. Also, was ich meinte war, dass für $ \ mathbb Q $ als Basisfeld $ x ^ 3-2 = 0 $ irreduzibel ist.
Betrachten wir $ x ^ 2 – 2x -1=0 $, um einige Hinweise zu erhalten. Diese Gleichung kann als irreduzibel erwiesen werden. Erinnerst du dich, wie man es löst?
Wenn $b^2-4ac \geq 0$, ja.
Genau! Die irreduzible Polynomgleichung $ x ^ 2 + 2x -1 = 0 $ hat also zwei Lösungen: $ 1 + \ sqrt {2} $ und $ 1- \ sqrt {2} $ … Irgendein Kommentar?
Bingo! Das ist die Schlüsselentdeckung von Galois. Im Allgemeinen konjugiert Galois alle Lösungen zu einer irreduziblen Polynomgleichung. Und wie Sie sich vorstellen können, sind diese wichtig, um Radikale aus den Nennern zu entfernen!
Das erste, was zu bemerken ist, ist, dass, wenn $ x_1 $, $ x_2 $, …, $ x_n $ alle Lösungen einer irreduziblen Polynomgleichung sind $a_n x ^ n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0 $ mit rationalen Koeffizienten, dann kann diese irreduzible Polynomgleichung tatsächlich umgeschrieben werden $a_n(x-x_1)(x-x_2)…( x-x_n)=0$. Das Identifizieren der konstanten Terme ergibt dann $x_1 x_2 … x_n $=$ (-1) ^n a_0/a_n $ . Entscheidend ist also, dass das Produkt konjugierter Zahlen die rationale Zahl $ (-1) ^ n a_0 / a_n $ ist, die ungleich Null ist (beweisen Sie es!).
Hier ist ein kleiner Witz, um die starke Verbindung zwischen Konjugaten im Auge zu behalten:

Betrachten Sie einen Bruch $1/x_1$, wobei $x_1$ ein komplizierter Ausdruck mit Radikalen ist. Multipliziert man nach oben und unten mit den Konjugaten $ x_2 $, …, $ x_n $ von $ x_1 $ ergibt sich dann $ 1 / x_1 $ = $ (-1) ^ n a_n x_2 … x_n / a_0 $, was kein Radikal im Nenner hat, da wir $ a_0 $ als eine von Null verschiedene Zahl des Basisfeldes festgelegt haben!
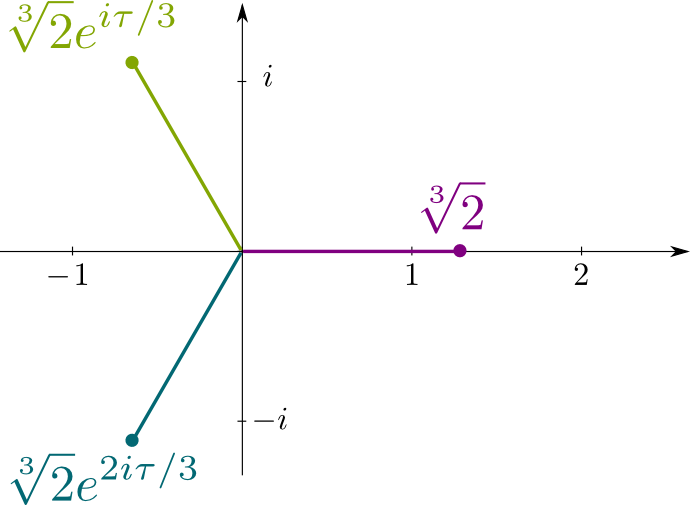
Denken Sie daran, dass $ x ^ 3-2=0 $ die irreduzible Polynomgleichung ist $\sqrt{2}$ ist die Lösung von. Seine Konjugate sind also die anderen Lösungen für diese Gleichung, nämlich die komplexen Zahlen $ \ sqrt {2} j $ und $ \ sqrt {2} j ^ 2 $, wobei $ j = e ^ {i \ tau / 3} $ mit $ \ tau = 2 \ pi $ das Verhältnis des Umfangs eines Kreises zu seinem Radius ist. Die folgende Abbildung zeigt die Positionen der konjugierten Lösungen in dieser komplexen Ebene:
Galois’Ambiguität
Endlich kommen wir zu Galois ‚wichtigsten Erkenntnissen!
Konjugate sind vollkommen permutierbar. Dies bedeutet, dass, wenn Sie $ \sqrt{2} $ systematisch durch sein Konjugat $ – \sqrt{2} $ ändern, die Gleichheit weiterhin gilt. Da wir zum Beispiel $1/(\sqrt{2}-1) = \sqrt{2}+1$ hatten, kann ich Ihnen ohne Weiteres sagen, dass $1/(-\sqrt{2}-1)=-\sqrt{2}+1$ ! In ähnlicher Weise haben wir die folgende erstaunliche Implikation:
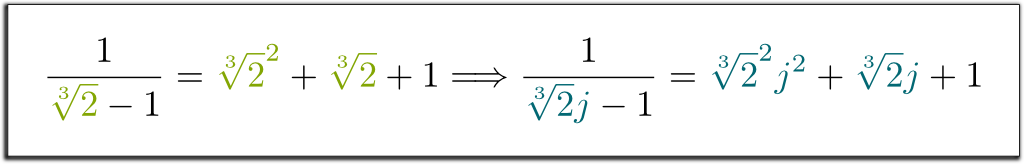
Hehe … Lassen Sie mich zuerst daran erinnern, dass endliche Felder von einem einzelnen Element überspannt werden. Wenn also das Basisfeld $ \ mathbb Q $ ist, kann jedes endliche Feld $ \ mathbb Q $ für ein rechtes $ x_1 $ geschrieben werden. Betrachten wir nun $ x ^ n + a_ {n-1} x ^ {n-1} $ +$ … + a_1 x + a_0 = 0 $ Die irreduzible Polynomgleichung $ x_1 $ ist die Lösung von. Was dann $ \ mathbb Q $ definiert, ist der $ \ mathbb Q $ -Vektorraum, der von $ x_1 $, $ x_1 ^ 2 $, …, $ x_1 ^ {n-1} $ , mit der Vereinfachung größerer Potenzen von $ x_1 $ entsprechend der algebraischen Regel $ x_1 ^ n $ = $ – a_ {n-1} x_1 ^ {n-1} $ -$ … – a_0 $.
Genau! Entscheidend ist, dass diese algebraischen Regeln von $ \ mathbb Q $ nicht wirklich von der Natur von $ x_1 $ abhängen; Sie hängen nur davon ab, dass das irreduzible Polynom $ x_1 $ die Lösung von ist! Daher sind die Regeln von $\mathbb Q$ identisch mit denen von $\mathbb Q$, …, $\mathbb Q$, wobei $x_1$ durch eines seiner Konjugate $x_2 $, …, $ x_n $ ersetzt wird. Insbesondere funktionieren die Felder $\mathbb Q{2}]$ und $\mathbb Q{2}j]$ entsprechend den exakt gleichen Regeln. Deshalb sind Konjugate perfekt permutierbar! Wir sagen, dass die Felder $ \mathbb Q{2}] $ und $ \mathbb Q{2} j]$ isomorph sind und dass das Ersetzen von $\sqrt{2}$ durch $\sqrt{2}j$ ein Isomorphismus $ \mathbb Q{2}] \rightarrow \mathbb Q{2}j] $ ist.
Auf eine sehr ähnliche (aber stärkere) Weise, dass zwei Vektorräume der Dimension 2 mehr oder weniger gleich sind! Dies hat schreckliche Folgen. Dies bedeutet, dass es aus algebraischer Sicht bedeutungslos ist, einen Unterschied zwischen einer Zahl und einem ihrer Konjugate zu machen (solange Sie die Zahl systematisch durch ihr Konjugat ersetzen)! So sind zum Beispiel $ \ sqrt{2} $ und $-\sqrt{2} $ algebraisch nicht zu unterscheiden! Um dies im Hinterkopf zu behalten, Hier ist ein weiterer Witz, den ich mir ausgedacht habe:

Überhaupt nicht! Jede Unterscheidung zwischen diesen beiden Zahlen muss eine andere Mathematik als die Algebra beinhalten, wie Ordnungsbeziehungen oder Topologie. Was ich meine ist, dass zum Beispiel die Beziehung $\sqrt{2} > 0$ einen Unterschied zwischen $\sqrt{2}$ und $ – \sqrt{2}$ , aber das liegt daran, dass es sich um eine Bestellbeziehung handelt. Wenn wir uns jedoch auf Polynomgleichungen beschränken, gibt es absolut keinen Unterschied zwischen $\sqrt{2}$ und $-\sqrt{2}$ . In ähnlicher Weise sind $ i $ und $ -i $, die Lösungen der irreduziblen Polynomgleichung $ x ^ 2 + 1 = 0 $, auch algebraisch nicht unterscheidbar. Dennoch nennen wir willkürlich $ i $ einen von ihnen. Deshalb nannte Galois seine Theorie die Theorie der Mehrdeutigkeit. Heute wird die Mehrdeutigkeit der Wahl der konventionellen Quadratwurzel von $ -1 $ unter $ i $ und $ -i $ eher als Symmetrie zwischen $ i $ und $ -i $ bezeichnet.
Galois-Gruppen
Galois konzentrierte sich besonders auf Felderweiterungen, die durch Konjugation stabil sind. Solche stabilen Felderweiterungen werden jetzt als Galois-Erweiterungen bezeichnet. Wenn also $ x_1 $ zu einer Galois-Erweiterung gehört, enthält diese Galois-Erweiterung alle ihre Konjugate $ x_2 $, …, $ x_n $.
Ein einfacher Weg, Galois-Erweiterungen zu konstruieren, besteht darin, das Feld zu nehmen, das von Lösungen einer irreduziblen Polynomgleichung überspannt wird. Wenn zum Beispiel $x_1 $, …, $x_n $ Konjugate für das Basisfeld $ \mathbb Q $ sind, dann ist $\mathbb Q / \mathbb Q $ eine Galois-Erweiterung. Felder, die auf diese Weise erstellt werden, werden als Splitting-Felder bezeichnet.
Zum Beispiel ist das Teilungsfeld der Gleichung $ x ^ 3-2=0 $ die Galois-Erweiterung $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q $, die von ihren Lösungen überspannt wird.
Wenn $x_1$ eine Galois-Erweiterung umspannt, dann auch seine Konjugate. Also $\mathbb Q = \mathbb Q =$ … $=\mathbb Q$ = $\mathbb Q$. Somit ist der Isomorphismus zwischen $ \ mathbb Q $ und $\mathbb Q $, der darin besteht, $ x_1 $ immer durch $ x_2 $ zu ersetzen, tatsächlich ein Isomorphismus zwischen $ \ mathbb Q $ und sich selbst! Wir nennen es Automorphismus. Automorphismen einer Galois-Erweiterung $\mathbb Q/\mathbb Q$ bilden die Galois-Gruppe $Gal(\mathbb Q/\mathbb Q)$.
Wenn nun $\mathbb Q = \mathbb Q$ , dann sind alle Automorphismen einer Galois-Erweiterung $\mathbb Q/ \mathbb Q$ Permutationen von $ x_1 $ mit einem seiner Konjugate! Insbesondere sehen wir hier, dass die Kardinalität einer Galois-Gruppe gleich dem Grad der Galois-Erweiterung ist.
Sicher! Sie können feststellen, dass $ \ mathbb Q = \ mathbb Q $ und $ \ mathbb Q = \ mathbb Q $ , was bedeutet, dass $ i $ und $ \ sqrt {2} $ jeweils die Teilungsfelder der irreduziblen Polynomgleichung umfassen, deren Lösung sie sind. Daher sind $ \ mathbb Q / \ mathbb Q $ und $ \ mathbb Q / \ mathbb Q $ beide Galois-Erweiterungen. Daher bestehen ihre Automorphismen darin, $ i $ durch eines ihrer Konjugate, $ i $ oder $ -i $, zu ersetzen und $ \ sqrt{2} $ durch $ \sqrt{2} $ oder $ – \ sqrt {2} $ zu ersetzen. In den ersten Fällen ändern wir nichts an Zahlen, was der Nullsymmetrie entspricht. Die zweiten Fälle können als Axialsymmetrien visualisiert werden, wie in der folgenden Abbildung dargestellt:

Ist das nicht erstaunlich?
Sicher! Kommen wir zum Teilungsfeld $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2]$ von $ x^ 3-2 = 0 $. Bevor wir jedoch weiter gehen, sollten wir beachten, dass $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$ .
Alles, was wir beweisen müssen, ist, dass alle Generatoren eines Feldes zum anderen gehören. Beginnen wir mit dem Beweis, dass die Generatoren der letzteren, $ \ sqrt{2} $ und $ j $, zu den ersteren gehören. Es ist offensichtlich für $\sqrt{2}$ . Nun, $j = (\sqrt{2} j) / \sqrt{2}$ , also gehört $ j $ auch zum ersteren Feld. Dies beweist, dass alle Elemente von $\mathbb Q{2},j]$ zu $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] $ gehören. Umgekehrt ist es einfach, dass alle Generatoren des ersteren Feldes, $ \ sqrt {2} $ , $ \ sqrt {2} j $ und $ \ sqrt {2} j ^ 2 $, Produkte der Generatoren des letzteren sind. Somit sind beide Felder gleich. Und insbesondere $ \mathbb Q{2}, j] /\mathbb Q$ ist eine Galois-Erweiterung.
Hehe … Um die Symmetrien von $ \ math [ Q{2}]$ zu verstehen, müssen wir in Galois ‚Studie über Galois-Gruppen weiter gehen …
Galois-Korrespondenz
Das Problem mit Galois-Gruppen ist, dass sie extrem groß und kompliziert werden können. Dies ist insbesondere der Fall bei der unendlichen Gruppe $Gal(\bar{\mathbb Q}/\mathbb Q)$. Um solche riesigen und komplexen Gruppen zu erfassen, hatte Galois die geniale Idee, diese in kleinere Stücke zu zerlegen.
Erstaunlicherweise fand Galois heraus, dass Galois-Gruppen in Untergruppen von Symmetrien unterteilt werden können, indem nur diejenigen betrachtet werden, die ein Unterfeld unverändert lassen. Zum Beispiel ist $ \ mathbb Q $ ein Unterfeld von $ \ mathbb Q{2},j] $, da eine beliebige Anzahl der ersteren zu letzterem gehört. Somit bilden Symmetrien von $\mathbb Q{2},j]$, die nichts an $\mathbb Q$ ändern, eine Untergruppe der Galois-Gruppe von $\mathbb Q{2},j]/\mathbb Q$. Diese Symmetrien bilden die Galois-Gruppe $Gal(\mathbb Q{2},j]/\mathbb Q)$.
Ich weiß! Ich mag es, diese Symmetrien als die Möglichkeiten zu visualisieren, $ \mathbb Q{2},j] $ auf $ \ mathbb Q $ zu stecken. Hier ist ein abgebildetes Bild des „Aufsteckens“:
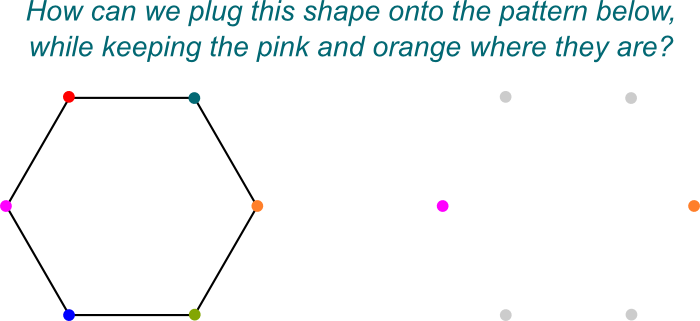
Genau! Und das liegt einfach daran, dass $\mathbb Q{2},j]$ eine Galois-Erweiterung von $\mathbb Q$ ist, die selbst eine Felderweiterung von $\mathbb Q$ .
Und es gibt noch mehr! Galois hat gezeigt, dass alle Untergruppen einer Galois-Erweiterung auf diese Weise erhalten werden! Genauer gesagt ist die Zuordnung eines beliebigen Feldes $K $ zwischen der Galois-Erweiterung $\mathbb Q{2},j] $ und dem Basisfeld $\mathbb Q$ zur Galois-Gruppe $Gal(\mathbb Q{2},j] / K) $ bijektiv. Diese Tatsache wird die Galois-Korrespondenz genannt! Diese Entsprechung wird unten schematisch für eine Galois-Erweiterung $\mathbb Q /\mathbb Q $ angezeigt.

Anstatt zu versuchen, diese Gruppe direkt zu beschreiben, konzentrieren wir uns auf ihre Untergruppe $Gal(\mathbb Q{2}, j]/\mathbb Q)$ . Es ist einfach, dass $ \sqrt{2} $ $ \mathbb Q{2},j] $ überspannt, wenn es zu $ \mathbb Q $ hinzugefügt wird. Somit ist $\mathbb Q{2},j]/\mathbb Q$ eine Galois-Erweiterung, die von $\sqrt{2}$ . Daher wissen wir anhand eines Satzes, den wir zuvor gesehen haben, dass alle Automorphismen dieser Galois-Erweiterung darin bestehen, $ \sqrt{2} $ durch eines seiner 3 Konjugate zu ersetzen (selbst $ \sqrt{2} j $ und $ \sqrt{2} j ^ 2 $)!
Jetzt könnte ich weiter andere Teile von $Gal(\mathbb Q{2}, j]/\mathbb Q)$ studieren, wie die Galois-Untergruppe $Gal(\mathbb Q{2},j]/\mathbb Q{2}])$ . Aber ich werde lieber einen anderen von Galois ‚mächtigen Theoremen verwenden. Er bewies nämlich, dass, wenn $ \mathbb Q /\mathbb Q $ zusätzlich eine Galois-Erweiterung selbst war, die Untergruppe $Gal(\mathbb Q{2}, j] /\mathbb Q) $ normal ist.Formal ist $H$ eine normale Untergruppe von $G$, wenn $gH = Hg$ für alle $g \in G$ ist.
Somit kann die Galois-Gruppe von $\mathbb Q{2},j]/\mathbb Q$ durch diese Untergruppe quotientiert werden, und die Quotientengruppe ist dann gleich $Gal(\mathbb Q/\mathbb Q)$. Dennoch ist $ \ mathbb Q / \ mathbb Q $ in der Tat eine Galois-Erweiterung, die von $ j $ überspannt wird und deren Konjugat $ j ^ 2 $ ist. Somit besteht $Gal(\mathbb Q/\mathbb Q) $ darin, $ j $ entweder als $ j $ zu belassen oder durch $ j ^ 2 $ zu ersetzen.
Wir können nun alle Symmetrien von $Gal(\mathbb Q{2},j]/\mathbb Q)$ableiten, indem wir diese von $Gal(\mathbb Q{2},j] / \mathbb Q)$ und $Gal(\mathbb Q/\mathbb Q) $ kombinieren. Wir können diese Symmetrien darstellen, indem wir zeichnen, wie sie unsere drei Spanning-Konjugate $\sqrt{2}$, $\sqrt{2}j$ und $\sqrt{2}j^2$ beeinflussen:
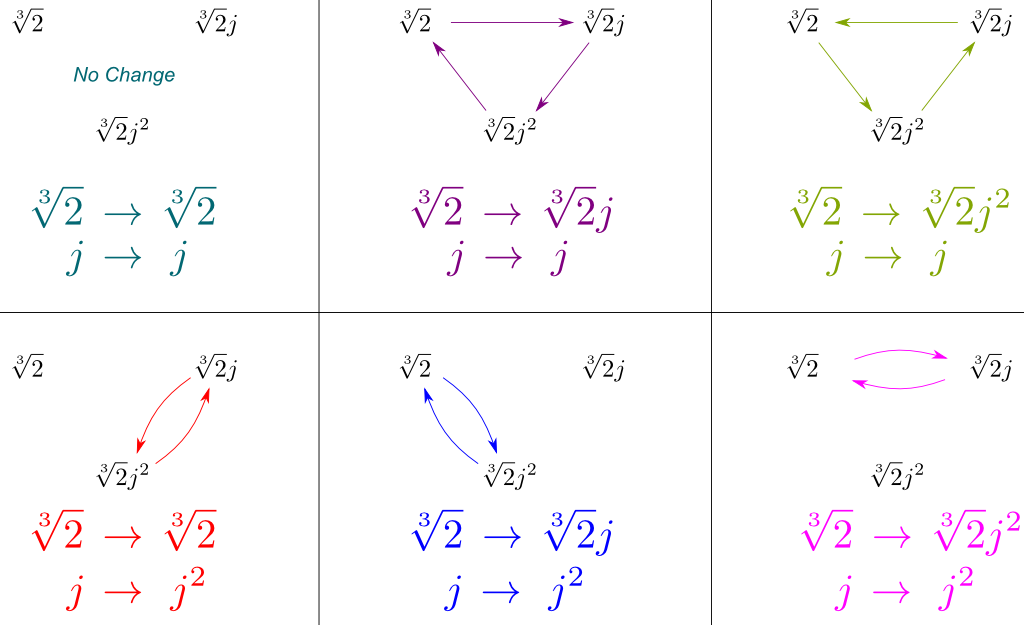
Entscheidend ist, dass die obige Abbildung alle Symmetrien von $Gal(\mathbb Q{2},j]/\mathbb Q)$ enthält. Und erstaunlicherweise entsprechen diese Symmetrien der bekannten Symmetriegruppe.
Ich lasse es Marcus du Sautoy präsentieren:
Also, sind Symmetrien hier wie ein Seestern oder wie ein Dreieck?
Ja, in der Tat! Diese Gruppe von Symmetrien des Dreiecks heißt $ D_3 $ und ist dieselbe wie die Gruppe $ S_3 $ von Permutationen von 3 Elementen. Dies führt uns zu der folgenden Formel, die ich so schön fand, dass ich beschlossen habe, sie einzurahmen!
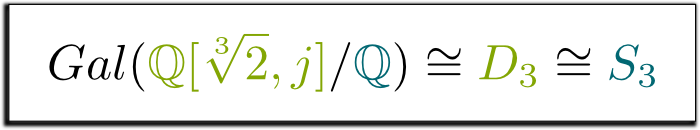
Schließen wir
In vielerlei Hinsicht ist Galois als der Vater der modernen Algebra zu betrachten. Seine wichtigste Erkenntnis war es, die Mathematik aus dem Blickwinkel der Operationsregeln zu betrachten, und dies führte ihn dazu, überraschende und aufschlussreiche Mehrdeutigkeiten oder Symmetrien zwischen Zahlen zu enthüllen. Aus algebraischer Sicht sind Zahlen wie $ \ sqrt {2} $, $ \ sqrt {2} j $ und $ \ sqrt {2} j ^ 2 $ in der Tat perfekt symmetrisch und völlig austauschbar.
Das Verständnis dieser Symmetrien hat unter anderem in der algebraischen Geometrie und algebraischen Topologie erstaunliche Anwendungen gefunden. Insbesondere umfassen frühe Erfolge der Theorie eine Klassifikation von konstruierbaren regelmäßigen Polygonen und ein Theorem, das behauptet, dass Polynomgleichungen hohen Grades nicht durch Radikale gelöst werden könnten.
Jüngste Erfolge zeigen sich in der Kryptographie und Andrew Wiles ‚Beweis für Fermats letzten Satz. Dieser Beweis beinhaltet das Studium der Galois-Gruppe $ Gal(\bar{\mathbb Q} /\mathbb Q) $ mit Gruppendarstellung. Aber ich würde sagen, dass die Theorie irgendwie noch jung ist und es noch viel zu entdecken gibt. Immerhin ist es eines der aktivsten Forschungsgebiete in der heutigen reinen Mathematikforschung.
Dies sollte uns dazu bringen, Galois ‚unglaublichem Genie noch viel mehr Tribut zu zollen … Lassen Sie mich eines von SocraticaStudios einschließen.