Frontiers in Genetics
Introduction
Die effektive Populationsgröße (Ne) ist ein wichtiger genetischer Parameter, der das Ausmaß der genetischen Drift in einer Population abschätzt und als die Größe einer idealisierten Wright–Fisher-Population beschrieben wurde, von der erwartet wird, dass sie den gleichen Wert eines bestimmten genetischen Parameters wie in der untersuchten Population ergibt (Crow und Kimura, 1970). Ne-Größen können durch Schwankungen der Populationsgröße (Nc), durch das Zuchtgeschlechtsverhältnis und die Varianz des Fortpflanzungserfolgs beeinflusst werden.Die Ne-Schätzung kann mit Ansätzen erreicht werden, die in drei methodische Kategorien fallen: demografisch, stammbaumbasiert oder markerbasiert (Flury et al., 2010). Stammbaumdaten wurden traditionell verwendet, um Ne-Schätzungen bei Nutztieren zu erhalten. Zuverlässige Schätzungen von Ne hängen jedoch davon ab, dass der Stammbaum vollständig ist. Dieser Wissensstand ist in einigen einheimischen Bevölkerungsgruppen möglich, deren demografische Parameter für eine ausreichend große Anzahl von Generationen genau überwacht wurden. In der Praxis bleibt die Anwendbarkeit dieses Ansatzes jedoch auf einige wenige Fälle bei stark bewirtschafteten Rassen beschränkt (Flury et al., 2010; Uimari und Tapio, 2011).Eine Lösung, um die Einschränkung eines unvollständigen Stammbaums zu überwinden, besteht darin, den jüngsten Trend bei Ne anhand genomischer Daten abzuschätzen. Mehrere Autoren haben erkannt, dass Ne aus Informationen über das Verknüpfungsungleichgewicht (LD) geschätzt werden kann (Sved, 1971; Hill, 1981). LD beschreibt die nicht-zufällige Assoziation von Allelen in verschiedenen Loci als Funktion der Rekombinationsrate zwischen den physikalischen Positionen der Loci im Genom. LD-Signaturen können jedoch auch aus demografischen Prozessen wie Beimischung und genetischer Drift (Wright, 1943; Wang, 2005) oder durch Prozesse wie „Trampen“ während selektiver Sweeps (Smith und Haigh, 1974) oder Hintergrundselektion (Charlesworth et al., 1997). In solchen Szenarien werden Allele an verschiedenen Loci unabhängig von ihrer Nähe im Genom assoziiert. Unter der Annahme, dass eine Population geschlossen und panmiktisch ist, hängt der zwischen neutralen, nicht verknüpften Loci berechnete LD-Wert ausschließlich von der genetischen Drift ab (Sved, 1971; Hill, 1981). Dieses Vorkommen kann verwendet werden, um Ne aufgrund der bekannten Beziehung zwischen der Varianz in LD (berechnet unter Verwendung von Allelfrequenzen) und der effektiven Populationsgröße vorherzusagen (Hill, 1981).
Jüngste Fortschritte in der Genotypisierungstechnologie (z., Verwendung von SNP-Bead-Arrays mit Zehntausenden von DNA-Sonden) haben die Sammlung großer Mengen genomweiter Verknüpfungsdaten ermöglicht, die sich ideal für die Schätzung von Ne bei Nutztieren und Menschen eignen (z. B. Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2010; Uimari und Tapio, 2011; Kijas et al., 2012). Forscher verlassen sich derzeit auf eine Kombination von Tools, um Daten zu manipulieren, LD abzuleiten und maßgeschneiderte Skripte zu verwenden, um die entsprechenden Berechnungen durchzuführen und Ne zu schätzen.
Hier beschreiben wir SNeP, ein Softwaretool, das die Schätzung von Ne-Trends über die Generation hinweg mithilfe von SNP-Daten ermöglicht, die Stichprobengröße, Phasenlage und Rekombinationsrate korrigieren.
Materialien und Methoden
Die Methode, mit der SNeP LD berechnet, hängt von der Verfügbarkeit von Phasendaten ab. Wenn die Phase bekannt ist, kann der Benutzer den quadratischen Korrelationskoeffizienten von Hill und Robertson (1968) auswählen, der Haplotypfrequenzen verwendet, um LD zwischen jedem Paar von Loci zu definieren (Gleichung 1). In Ermangelung einer bekannten Phase kann jedoch der quadratische Pearson-Produkt-Moment-Korrelationskoeffizient zwischen Paaren von Loci ausgewählt werden. Diese beiden Ansätze sind zwar nicht gleich, aber in hohem Maße vergleichbar (McEvoy et al., 2011):
wobei pA und pB jeweils die Frequenzen der Allele A und B an zwei getrennten Loci (X, Y) sind, gemessen für n Individuen, ist pAB die häufigkeit des Haplotyps mit Allelen A und B in der untersuchten Population, X und Y sind die mittleren Genotyphäufigkeiten für den ersten bzw. zweiten Locus, Xi ist der Genotyp von Individuum i am ersten Locus und Yi ist der Genotyp von Individuum i am zweiten Locus. Gleichung (2) korreliert die genotypischen Allelzahlen anstelle der Haplotyphäufigkeiten und wird nicht durch doppelte Heterozygoten beeinflusst (dieser Ansatz führt zu denselben Schätzungen wie die Option –r2 in PLINK).SNeP schätzt die historische effektive Populationsgröße basierend auf der Beziehung zwischen r2, Ne und c (Rekombinationsrate) (Gleichung 3-Sved, 1971) und ermöglicht es Benutzern, Korrekturen für die Stichprobengröße und Unsicherheit der gametischen Phase (Gleichung 4—Weir und Hill, 1980):
wobei n die Anzahl der einzelnen abgetasteten ist, β = 2, wenn die gametische Phase bekannt ist, und β = 1, wenn stattdessen die Phase nicht bekannt ist.
Mehrere Näherungen werden verwendet, um die Rekombinationsrate unter Verwendung des physikalischen Abstands (δ) zwischen zwei Loci als Referenz abzuleiten und in einen Abstand (d) zu übersetzen, der normalerweise als Mb(δ) ≈ cM(d) beschrieben wird. Für kleine Werte von d gilt die letztgenannte Näherung, für größere Werte von d steigt jedoch die Wahrscheinlichkeit mehrfacher Rekombinationsereignisse und Interferenzen, außerdem ist das Verhältnis zwischen Kartenabstand und Rekombinationsrate nicht linear, da die maximal mögliche Rekombinationsrate 0,5 beträgt. Daher ist die Approximation d ≈ c, sofern nicht sehr kurze δ verwendet werden, nicht ideal (Corbin et al., 2012). Wir haben daher Mapping-Funktionen implementiert, um das geschätzte d in c zu übersetzen, nach Haldane (1919), Kosambi (1943), Sved (1971) und Sved und Feldman (1973). Anfänglich leitet SNeP d für jedes Paar von SNPs als direkt proportional zu δ gemäß d = kδ ab, wobei k ein benutzerdefinierter Rekombinationsratenwert ist (Standardwert ist 10-8 wie in Mb = cM). Der abgeleitete Wert von δ kann dann bei Bedarf durch den Benutzer einer der verfügbaren Abbildungsfunktionen unterzogen werden.
Das Lösen von Gleichung (3) für Ne und einschließlich aller beschriebenen Korrekturen ermöglicht die Vorhersage von Ne aus LD-Daten unter Verwendung von (Corbin et al., 2012):
wobei Nt die effektive Populationsgröße t vor Generationen ist, berechnet als t = (2f(ct))-1 (Hayes et al., 2003), ct ist die Rekombinationsrate, die für einen bestimmten physikalischen Abstand zwischen Markern definiert und optional mit den oben genannten Abbildungsfunktionen angepasst wurde, r2adj ist der für die Probengröße bereinigte LD-Wert und α: = {1, 2, 2.2} ist eine Korrektur für das Auftreten von Mutationen (Ohta und Kimura, 1971). Daher ist LD über größere rekombinante Entfernungen informativ für die jüngsten Ne, während kürzere Entfernungen Informationen über weiter entfernte Zeiten in der Vergangenheit liefern. Ein Binning-System wird implementiert, um gemittelte r2-Werte zu erhalten, die LD für bestimmte Interlocus-Entfernungen widerspiegeln. Das implementierte Binning-System verwendet die folgende Formel, um die Minimal- und Maximalwerte für jeden Behälter zu definieren:
Wobei bi (ℕ1) der i-te Behälter der Gesamtzahl der Behälter (totBins) ist, sind minD und maxD jeweils der minimale und der maximale Abstand zwischen SNPs und x ein positiver reelle Zahl (ℝ0) Wenn x gleich 1 ist, ist die Verteilung der Abstände zwischen den Behältern linear und jeder Behälter hat den gleichen Abstandsbereich. Bei größeren Werten von x ändert sich die Verteilung der Abstände, was einen größeren Bereich in den letzten Bins und einen kleineren Bereich in den ersten Bins ermöglicht. Durch Variieren dieses Parameters kann der Benutzer über eine ausreichende Anzahl von paarweisen Vergleichen verfügen, um zur endgültigen Ne-Schätzung für jeden Behälter beizutragen.
Beispielanwendung
Wir haben SNeP mit zwei veröffentlichten Datensätzen getestet, die zuvor verwendet wurden, um Trends in Ne im Laufe der Zeit mit LD, Bos indicus und Ovis aries zu beschreiben . Die r2-Schätzungen für die Rinderdatensätze wurden von den Autoren unter Verwendung von GenABLE (Aulchenko et al., 2007) unter Verwendung einer minimalen Allelfrequenz (MAF) < 0,01 und Einstellen der Rekombinationsrate unter Verwendung der Haldane-Mapping-Funktion (Haldane, 1919). Die r2-Schätzungen der Schafdaten wurden von den Autoren unter Verwendung von PLINK-1.07 (Purcell et al., 2007), mit einem MAF < 0.05 und ohne weitere Korrekturen. Für beide autosomalen Datensätze wurden die r2-Schätzungen unter Verwendung von Gleichung (4) mit β = 2 um die Stichprobengröße korrigiert. Für diese vergleichenden Analysen enthielt die SNeP-Befehlszeile dieselben Parameter, die für die veröffentlichten Daten verwendet wurden, abgesehen von den r2-Schätzungen, die durch die Genotypzählung und die Verwendung der neuartigen SNEP-Binning-Strategie berechnet wurden.
Ergebnisse
SNeP ist eine Multithread-Anwendung, die in C ++ entwickelt wurde und Binärdateien für die gängigsten Betriebssysteme (Windows, OSX und Linux) von https://sourceforge.net/projects/snepnetrends/ heruntergeladen werden können. Die Binärdateien werden von einem Handbuch begleitet, das die schrittweise Verwendung von SNeP beschreibt, um Trends in Ne abzuleiten, wie hier beschrieben. SNeP erzeugt eine Ausgabedatei mit tabulatorgetrennten Spalten, die für jeden Bin, der zur Schätzung von Ne verwendet wurde, Folgendes anzeigen: die Anzahl der Generationen in der Vergangenheit, denen der Bin entspricht (z., vor 50 Generationen), die entsprechende Ne-Schätzung, der durchschnittliche Abstand zwischen jedem SNP-Paar im Bin, der durchschnittliche r2 und die Standardabweichung von r2 im Bin sowie die Anzahl der SNPs, die zur Berechnung von r2 im Bin verwendet werden. Diese Datei kann einfach in Microsoft Excel, R oder andere Software importiert werden, um die Ergebnisse zu zeichnen. Die hier gezeigten Diagramme (Abbildungen 1, 3) entsprechen den Spalten von generations ago und Ne aus der Ausgabedatei. Die Spalte mit der r2-Standardabweichung wird bereitgestellt, damit Benutzer die Varianz in der Ne-Schätzung in jedem Bin überprüfen können, insbesondere für diejenigen Bins, die ältere Zeitschätzungen widerspiegeln und die weniger zuverlässig sind, da die Anzahl der SNPs, die zur Schätzung von r2 verwendet werden, kleiner wird.
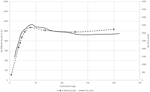
Abbildung 1. Vergleich der Ne-Trends von sechs Schweizer Schafrassen nach Burren et al. (2014) (gestrichelte Linien) und diese Arbeit (durchgezogene Linien).
Das für die Eingabedateien erforderliche Format ist das Standard-PLINK-Format (Ped- und Map-Dateien) (Purcell et al., 2007). SNeP ermöglicht es den Benutzern, entweder LD auf den Daten wie oben beschrieben zu berechnen oder eine benutzerdefinierte vorberechnete LD-Matrix zu verwenden, um Ne unter Verwendung von Gleichung (5) zu schätzen.
Die Software-Schnittstelle ermöglicht es dem Benutzer, alle Parameter der Analyse zu steuern, z. B. den Abstandsbereich zwischen SNPs in bp und dem in der Analyse verwendeten Chromosomensatz (z. B. 20-23). Zusätzlich enthält SNeP die Option, einen MAF-Schwellenwert zu wählen (Standardwert 0.05), da gezeigt wurde, dass die Berücksichtigung von MAF unabhängig von der Stichprobengröße zu unvoreingenommenen r2-Schätzungen führt (Sved et al., 2008). Die Multithread-Architektur von SNeP ermöglicht die schnelle Berechnung großer Datensätze (wir haben bis zu ~ 100K SNPs für ein einzelnes Chromosom getestet), zum Beispiel wurden die hier beschriebenen BOS-Daten mit einem Prozessor in 2’43 „analysiert, die Verwendung von zwei Prozessoren reduzierte die Zeit auf 1’43 „, vier Prozessoren reduzierten die Analysezeit auf 1’05 „.
Zebu-Beispiel
Für die zebu-Analyse zeigten die Formen der mit SNeP erhaltenen Ne-Kurven und ihre veröffentlichten Datentrends die gleiche Flugbahn mit einem sanften Rückgang bis vor etwa 150 Generationen, gefolgt von einer Expansion mit einem Höhepunkt vor etwa 40 Generationen und einem steilen Rückgang bei den jüngsten Generationen (Abbildung 1). Obwohl die Trends in beiden Kurven gleich waren, führten die beiden Ansätze zu unterschiedlichen Ne-Schätzungen, wobei die SNeP-Werte ungefähr dreimal größer waren als die in der Originalarbeit. Während wir versuchten, die Parameter der Autoren in unseren Analysen zu verwenden, waren einige Unterschiede unvermeidlich, dh die ursprüngliche Veröffentlichung der Rinderdaten schätzte r2 mit einem anderen Ansatz als in SNeP implementiert. Analysen mit SNeP basierten auf Genotypen, während die ursprüngliche Analyse auf abgeleiteten zwei Locus-Haplotypen basierte, was dazu führte, dass die veröffentlichten Daten einen erwarteten r2 von 0,32 im Mindestabstand zeigten, während unsere Schätzungen 0,23 betrugen. In ähnlicher Weise Mbole-Kariuki et al. (2014) erhielt einen Hintergrundpegel r2 = 0,013 um 2 Mb, während unsere Schätzung in der gleichen Entfernung 0 war.0035 (Daten nicht dargestellt). Folglich, da unsere Schätzungen von LD durchweg kleiner waren als Mbole-Kariuki et al. (2014) es wird erwartet, dass unsere Ne-Schätzungen größer sein sollten. Diese Beobachtung unterstreicht zwar die Bedeutung einer sorgfältigen Auswahl der Parameter und ihrer Schwellenwerte, es ist jedoch wichtig hervorzuheben, dass die Trends nahezu identisch sind, obwohl die absolute Größe der Ne-Werte unterschiedlich ist.
Beispiel Schweizer Schafe
Die sechs mit SNeP analysierten Schweizer Schafrassen ergaben vergleichbare Ergebnisse mit denen aus der Originalarbeit (Abbildung 2), wobei sich die Ne-Trendkurven größtenteils überlappen (Abbildung 3). Der allgemeine Trend in Ne zeigte jedoch einen Rückgang in Richtung Gegenwart. SNeP erzeugte etwas größere Werte von Ne für die weiter entfernte Vergangenheit (700-800 Generationen). Dies ist auf das in SNeP verwendete unterschiedliche Binning-System zurückzuführen, das es dem Benutzer ermöglicht, eine gleichmäßigere Verteilung der paarweisen Vergleiche innerhalb jedes Bin (d. h., die Anzahl der SNP-paarweisen Vergleiche in jedem Bin ist vergleichbar). Für die Zeitspanne, die sich über 400 Generationen hinaus erstreckt, Burren et al. (2014) verwendeten in ihrer Analyse nur drei Bins (zentriert auf 400, 667 und 2000 Generationen), während SNeP für die gleiche Zeitspanne 5 Bins mit einer Anzahl von paarweisen Vergleichen verwendete, die von dem mit den Formeln 6a, b definierten Bereich abhängig waren. Daher neigt die Verwendung von weniger Behältern dazu, das Vorhandensein kleinerer Ne-Werte in jedem Behälter zu erhöhen, wodurch der durchschnittliche Ne-Wert für jeden Behälter verringert wird. Die Ne-Werte für die jüngste Vergangenheit, verglichen mit der 29. Generation in der Vergangenheit, ergaben sehr ähnliche Ergebnisse. Der größte Unterschied (50) wurde für die SBS-Rasse erhalten.

Abbildung 2. Vergleich zwischen den jüngsten Ne-Werten, die in dieser Arbeit bei der 29. (2014) für sechs Schweizer Schafrassen.
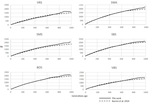
Abbildung 3. Vergleich der Ne-Trends der letzten 250 Generationen in den SHZ-Daten von Mbole-Kariuki et al. (2014) (gestrichelte Linie) und mit SNeP (durchgezogene Linie).
Diskussion
Die Analyse von Ne anhand von LD-Daten wurde erstmals vor 40 Jahren demonstriert und seitdem angewendet, entwickelt und verbessert (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Die traditionell geringe Anzahl der analysierten SNPs ist keine Einschränkung mehr, da SNP-Chips eine extrem große Anzahl von SNPs umfassen, die in kurzer Zeit und zu einem vernünftigen Preis verfügbar sind. Dies hat die Anwendung der Methode, die auf den Menschen angewendet wurde, verstärkt (Tenesa et al., 2007; McEvoy et al., 2011) sowie zu mehreren domestizierten Arten (England et al., 2006; Uimari und Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Zusammen mit diesen Verbesserungen sind methodische Einschränkungen offensichtlich geworden und wurden hier angegangen, wobei der Großteil der Bemühungen auf die korrekte Schätzung der jüngsten Ne hinweist. Der quantitative Wert der Schätzung hängt jedoch stark von der Stichprobengröße, der Art der LD-Schätzung und dem Binning-Prozess ab (Waples und Do, 2008; Corbin et al., 2012), während sein qualitatives Muster mehr von der genetischen Information als von der Datenmanipulation abhängt.
Bisher wurde diese Methode unter Verwendung einer Vielzahl von Software angewendet, es gibt keinen standardisierten Ansatz zur Bindung der Ergebnisse und jede Studie hat einen mehr oder weniger willkürlichen Ansatz angewendet, z. B. Binning für Generationsklassen in der Vergangenheit (Corbin et al., 2012), Binning für Distanzklassen mit konstanter Reichweite für jeden Bin (Kijas et al., 2012) oder Binning pro Entfernungsklasse linear, jedoch mit größeren Bins für die neueren Zeitpunkte (Burren et al., 2014). Unseres Wissens ist die einzige verfügbare Software, die Ne durch LD schätzt, NeEstimator (Do et al., 2014), eine aktualisierte Version des ehemaligen LDNE (Waples und Do, 2008), die die Analyse großer Datensätze (als 50k SNPChip) ermöglicht. Während sich SNeP auf die Schätzung historischer Ne-Trends konzentriert, ist es Neestimators Ziel, zeitgenössische unvoreingenommene Ne-Schätzungen zu erstellen, die daher als ergänzendes Instrument bei der Untersuchung der Demographie durch LD betrachtet werden sollten.
Wir haben SNeP verwendet, um zwei Datensätze zu analysieren, in denen die Methode zuvor angewendet wurde. Die Ergebnisse, die wir für die Schafdaten erhielten, waren sowohl quantitativ als auch qualitativ vergleichbar mit denen von Burren et al. (2014), während wir für die Zebu-Daten eine Ne-Trendschätzung erhielten, die der von Mbole-Kariuki et al. (2014) obwohl unsere Punktschätzungen von Ne größer waren als die für die Daten beschriebenen (Mbole-Kariuki et al., 2014). Die Diskrepanz zwischen diesen beiden Ergebnissen spiegelt wider, dass Burren und Kollegen ihre r2-Schätzungen mit PLINK (der Standardsoftware für die SNP-Datenmanipulation in großem Maßstab) erstellt haben, die denselben Ansatz verwendet, um r2 von SNeP zu schätzen, während Mbole-Kariuki et al. gefolgt von Hao et al. (2007) für r2 Schätzung. Die Verwendung unterschiedlicher Schätzungen für LD ist entscheidend für den quantitativen Aspekt der Ne-Kurve, wo aufgrund der hyperbolischen Korrelation zwischen Ne und r2 Eine Abnahme von r2 in seinem Bereich näher an 0 zu einer sehr großen Änderung der Ne-Schätzungen führen kann, während Unterschiede in Schätzungen sind weniger signifikant, wenn der r2-Wert hoch ist, d. H. Näher an 1. Obwohl in einem der Datensätze die Ne-Werte wesentlich unterschiedlich waren, überlappten sich daher in beiden Fällen die Ne-Kurven mit den ursprünglich veröffentlichten.
Wie bereits von anderen Autoren vorgeschlagen, ist die Zuverlässigkeit der mit dieser Methode erhaltenen quantitativen Schätzungen mit Vorsicht zu genießen, insbesondere für Ne-Werte, die sich auf die jüngste und älteste Generation beziehen (Corbin et al., 2012), weil für die letzten Generationen große Werte von c beteiligt sind, die nicht zu den theoretischen Implikationen passen, die Hayes vorgeschlagen hat, um eine Variable Ne im Laufe der Zeit abzuschätzen (Hayes et al., 2003). Schätzungen für die ältesten Generationen könnten auch unzuverlässig sein, da die Koaleszenztheorie zeigt, dass nach 4Ne-Generationen in der Vergangenheit kein SNP zuverlässig beprobt werden kann (Corbin et al., 2012). Des Weiteren, Ne-Schätzungen, und insbesondere diejenigen, die sich auf Generationen weiter in der Vergangenheit beziehen, werden stark von Datenmanipulationsfaktoren beeinflusst, wie die Wahl von MAF- und Alpha-Werten. Darüber hinaus kann die angewendete Binning-Strategie die allgemeine Genauigkeit des Verfahrens beeinträchtigen, beispielsweise wenn eine unzureichende Anzahl von paarweisen Vergleichen verwendet wird, um jeden Bin zu füllen.
Eine der Anwendungen der Methode ist der Vergleich von Rassedemographien. In diesem Fall wäre die Form der Ne-Kurven das optimale Werkzeug, um verschiedene demografische Geschichten mehr als ihre numerischen Werte zu unterscheiden, indem sie als potenzieller demografischer Fingerabdruck für diese Rasse oder Art verwendet werden, wobei jedoch berücksichtigt wird, dass Mutation, Migration und Selektion die Ne-Schätzung durch LD beeinflussen können (Waples und Do, 2010). Darüber hinaus ist eine sorgfältige Betrachtung der mit SNeP (und anderer Software zur Schätzung von Ne) analysierten Daten sehr wichtig, da das Vorhandensein von Störfaktoren wie Beimischung zu voreingenommenen Schätzungen von Ne führen kann (Orozco-terWengel und Bruford, 2014).Das Ziel von SNeP ist es daher, ein schnelles und zuverlässiges Werkzeug zur Verfügung zu stellen, um LD-Methoden anzuwenden, um Ne unter Verwendung von genotypischen Daten mit hohem Durchsatz konsistenter abzuschätzen. Es ermöglicht zwei verschiedene r2-Schätzansätze sowie die Möglichkeit, r2-Schätzungen aus externer Software zu verwenden. Die Verwendung von SNeP überwindet nicht die Grenzen der Methode und der Theorie dahinter, ermöglicht es dem Benutzer jedoch, die Theorie unter Verwendung aller bisher vorgeschlagenen Korrekturen anzuwenden.
Autorenbeiträge
MB konzipierte und schrieb die Software und das Manuskript. MB, MT und POtW testeten die Software und führten die Analysen durch. MT, POtW und MWB überarbeiteten das Manuskript. Alle Autoren stimmten dem endgültigen Manuskript zu.
Erklärung zum Interessenkonflikt
Die Autoren erklären, dass die Forschung in Abwesenheit von kommerziellen oder finanziellen Beziehungen durchgeführt wurde, die als potenzieller Interessenkonflikt ausgelegt werden könnten.
Danksagung
Wir danken Christine Flury für die Bereitstellung der Schaf-Daten und für die nützliche Diskussion. Wir danken auch den beiden Gutachtern für nützliche Vorschläge zur Verbesserung dieses Papiers. MB wurde vom Programm Master and Back (Regione Sardegna) unterstützt.
Charlesworth, B., Nordborg, M. und Charlesworth, D. (1997). Die Auswirkungen der lokalen Selektion, ausgewogener Polymorphismus und Hintergrundselektion auf Gleichgewichtsmuster der genetischen Vielfalt in unterteilten Populationen. Genet. 70, 155-174. doi: 10.1017/S0016672397002954
PubMed Zusammenfassung | Volltext | CrossRef Volltext / Google Scholar
Crow, JF und Kimura, M. (1970). Eine Einführung in die Populationsgenetik Theorie. New York, NY: Harper und Row.
Google Scholar
Ohta, T. und Kimura, M. (1971). Verknüpfungsungleichgewicht zwischen zwei segregierenden Nukleotidstellen unter dem stetigen Fluss von Mutationen in einer endlichen Population. Genetik 68, 571-580.
PubMed Zusammenfassung | Volltext / Google Scholar
Wright, S. (1943). Isolation durch Distanz. Genetik 28, 114-138.
PubMed Zusammenfassung / Volltext / Google Scholar