Die Brechung oder Biegung von Licht tritt auf, wenn Licht von einem Medium in ein anderes Medium mit einem anderen Brechungsindex übergeht. Die Brechung ist eine wichtige Eigenschaft von Linsen, die es ihnen ermöglicht, einen Lichtstrahl auf einen einzelnen Punkt zu fokussieren, und ist auch für eine Vielzahl bekannter Phänomene verantwortlich, wie z. B. die scheinbare Verzerrung von Objekten, die teilweise in Wasser eingetaucht sind.

Der Brechungsindex ist definiert als die relative Geschwindigkeit, mit der sich Licht in Bezug auf seine Geschwindigkeit im Vakuum durch ein Material bewegt. Konventionell ist der Brechungsindex eines Vakuums mit einem Wert von 1,0 definiert. Der Brechungsindex n anderer transparenter Materialien wird durch die Gleichung definiert:

wobei c die Lichtgeschwindigkeit und v die Lichtgeschwindigkeit in diesem Material ist. Da der Brechungsindex eines Vakuums als 1 definiert ist.0 und ein Vakuum ist frei von jeglichem Material, die Brechungsindizes aller transparenten Materialien sind daher größer als 1,0. Für die meisten praktischen Zwecke kann der Brechungsindex von Licht durch Luft (1,0003) verwendet werden, um Brechungsindizes unbekannter Materialien zu berechnen. Die Brechungsindizes einiger gängiger Materialien sind in der folgenden Tabelle 1 dargestellt.

Material Brechungsindex Luft 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Wenn beispielsweise Licht von einem weniger dichten Medium wie Luft zu einem dichteren Medium wie Wasser gelangt, nimmt die Geschwindigkeit ab, mit der sich die elektromagnetische Welle bewegt. Alternativ, wenn Licht von einem dichteren Medium zu einem weniger dichten Medium übergeht, erhöht sich die Geschwindigkeit der Welle.

Der Winkel, unter dem sich das gebrochene Licht bewegt, ist jedoch sowohl vom Einfallswinkel als auch von der Zusammensetzung des Materials abhängig, in das es eintritt. Die Normale kann als eine Linie senkrecht zur Grenze zwischen zwei Substanzen definiert werden. Licht tritt in einem Winkel zur Normalen in die Grenze ein und wird nach dem Snellschen Gesetz gebrochen:

wobei n die Brechungsindizes von Material 1 und Material 2 darstellt und q die Lichtwinkel symbolisiert, die durch diese Materialien in Bezug auf die Normale wandern. Es gibt mehrere wichtige Punkte, die aus dieser Gleichung gezogen werden können. Wenn n(1) größer als n(2) ist, ist der Brechungswinkel immer kleiner als der Einfallswinkel. Alternativ ist, wenn n(2) größer als n(1) ist, der Brechungswinkel immer größer als der Einfallswinkel. Wenn die beiden Brechungsindizes gleich sind (n (1) = n (2)), wird das Licht ohne Brechung durchgelassen.

Das Konzept des Brechungsindex ist in Abbildung 1 unten dargestellt, wobei der Schwerpunkt auf dem Fall liegt, dass Licht von Luft durch Glas und Wasser strömt. Beachten Sie, dass, während beide Strahlen durch den gleichen Einfallswinkel in Bezug auf die Normale (60 Grad) in das dichtere Material eintreten, die Brechung für Glas aufgrund des höheren Brechungsindex von Glas fast 6 Grad größer ist als für Wasser.

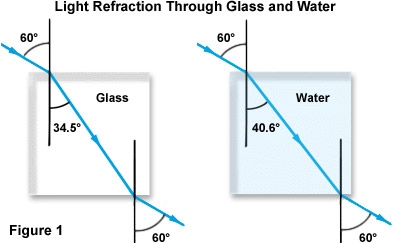
Wissenschaftler haben herausgefunden, dass der Brechungsindex mit der Frequenz der Strahlung (oder Wellenlänge) des Lichts variiert. Dieses Phänomen tritt in Verbindung mit allen transparenten Medien auf und wurde als Dispersion bezeichnet. Daher muss bei der Messung des Brechungsindex einer transparenten Substanz die bei der Messung verwendete Wellenlänge identifiziert werden. Tabelle 2 zeigt die Dispersion von drei unabhängigen Wellenlängen in verschiedenen Medien.

Material Blau (486,1 nm) Gelb (589,3 nm) Rot (656,3 nm) Krone Glas 1,524 1,517 1,515 Flint Glas 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Dieses Licht wird als D-Linien-Spektrum bezeichnet und stellt das in der obigen Tabelle 2 aufgeführte gelbe Licht dar. Ebenso entsprechen F-Linien- und C-Linien-Spektren blauem und rotem Licht bestimmter Wellenlängen, die von Wasserstoff emittiert werden. Diese Spektren sind grundlegend für die Berechnung der Dispersion, die quantitativ definiert werden kann als:

wobei n der Brechungsindex des Materials bei einer bestimmten Wellenlänge ist, die mit D, F und C bezeichnet ist, die die Spektrallinien von Natrium und Wasserstoff darstellen, wie oben. Die Beziehung ist so, dass mit zunehmender Wellenlänge des Lichts der Brechungsindex abnimmt. Bei der Dispersion verschiedener Materialien spielen jedoch viele Faktoren eine Rolle, einschließlich ihrer elementaren und molekularen Zusammensetzung. Mehrere anorganische Feststoffe, wie Chromate, Dichromate, Cyanide, Vanadate und Halogenidkomplexe, weisen ungewöhnlich hohe Dispersionen auf. Organische Substituenten können aber auch zu einer hohen Dispersion beitragen.

	Interactive Java Tutorial
Brechung von Licht Entdecken Sie, wie die Wellenlänge und der Einfallswinkel von Licht die Brechung in einer Vielzahl von Medien mit unterschiedlichen Brechungsindizes beeinflussen.

Refraction of light is particularly important in the construction and physics of lenses. Denken Sie daran, dass der Lichtstrahl, als er in Abbildung 1 sowohl das Glas als auch das Wasser verließ, erneut in demselben Winkel gebrochen wurde, in dem er in das Material eindrang. Dieses Konzept ist für die Funktion von Objektiven von wesentlicher Bedeutung, obwohl die Form der Linse das resultierende Bild erheblich beeinflusst. In einer konvexen Linse, wie unten in Abbildung 2 dargestellt, werden vom Objekt reflektierte Lichtwellen, in diesem Fall eine Giraffe, zum optischen Zentrum der Linse hin gebogen und konvergieren auf dem Brennpunkt.

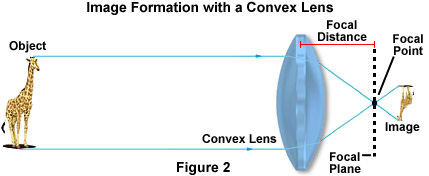
Die relative Position des Objekts in Bezug auf den vorderen Brennpunkt des Objektivs bestimmt, wie das Objekt abgebildet wird. Wenn das Objekt die doppelte Länge des Brennpunkts überschreitet, erscheint es kleiner und invertiert und muss von einer zusätzlichen Linse abgebildet werden, um die Größe zu vergrößern. Wenn sich das Bild jedoch näher am Objektiv als am Brennpunkt befindet, erscheint das Bild aufrecht und größer, wie mit einer einfachen Lupe leicht demonstriert werden kann.

	Interactive Java Tutorial
Bildvergrößerung Untersuchen Sie, wie das Bild einer Giraffe durch Brechung von Lichtwellen vergrößert wird, die durch eine einfache dünne bikonvexe Linse gelangen.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Ein einfacher Trinkhalm in einem mit Wasser gefüllten Glas, wie in Abbildung 3 dargestellt, ist ein Paradebeispiel für dieses Ereignis. In diesem Beispiel müssen Lichtwellen zuerst durch das Wasser, dann durch die Glas-Wasser-Grenze und schließlich durch die Luft gehen. Die von den Enden des Strohhalms reflektierten Lichtwellen werden stärker gebrochen als die von der Mitte des Strohhalms kommenden, wodurch das Stroh vergrößert und leicht verzerrt erscheint.

Das gleiche Phänomen kann verwendet werden, um den Brechungsindex einer Flüssigkeit mit einem optischen Mikroskop zu bestimmen. Dazu muss eine flache Zelle, die Flüssigkeit mit einer Markierung (oder Abstufungen) aufnehmen kann, auf der inneren Glasoberfläche angebracht werden. Außerdem muss eines der Mikroskopokulare ein abgestuftes Fadenkreuz haben, das an der primären Bildebene für Linienbreitenmessungen der Markierung in der flachen Zelle eingefügt ist. Bevor die Flüssigkeit mit unbekanntem Brechungsindex in die Zelle gegeben wird, sollte das Mikroskop auf die Markierung am Boden der Zelle fokussiert und eine Messung der Position der Markierung auf dem Fadenkreuz notiert werden. Als nächstes sollte eine kleine Menge Flüssigkeit in die Zelle gegeben und das Mikroskop auf die Markierung (durch die Flüssigkeit) fokussiert und eine neue Messung durchgeführt werden. Das Mikroskop sollte dann schließlich auf die Oberfläche der Flüssigkeit fokussiert werden, und ein dritter Messwert wird aufgezeichnet, indem die Position der Markierung auf dem Fadenkreuz gemessen wird. Der Brechungsindex der unbekannten Flüssigkeit kann dann unter Verwendung der folgenden Gleichung berechnet werden:

wobei D(gemessen) die gemessene Tiefe (von der Oberfläche der Flüssigkeit bis zur Position der Markierung auf der leeren Zelle) unter Verwendung des Mikroskops und D(offensichtlich) die Markierungsmessung mit und ohne Flüssigkeit ist.

Der kritische Reflexionswinkel ist ein weiteres Schlüsselkonzept bei der Untersuchung der Lichtbrechung und wird unten in Abbildung 4 dargestellt. Wenn Licht durch ein Medium mit hohem Brechungsindex in ein Medium mit niedrigerem Brechungsindex gelangt, wird der Einfallswinkel der Lichtwellen zu einem wichtigen Faktor. Wenn der Einfallswinkel über einen bestimmten Wert hinaus zunimmt (abhängig vom Brechungsindex der beiden Medien), erreicht er einen Punkt, an dem der Winkel so groß ist, dass kein Licht in das Medium mit niedrigerem Brechungsindex gebrochen wird.

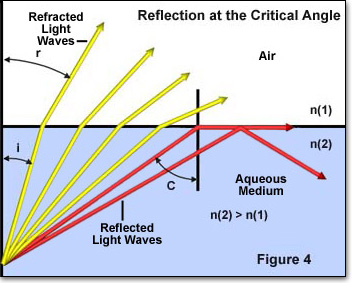
In Abbildung 4 werden einzelne Lichtstrahlen entweder durch rote oder gelbe Pfeile dargestellt, die sich von einem Medium mit hohem Brechungsindex (n(2)) zu einem Medium mit niedrigerem Brechungsindex (n(1)) bewegen. Der Einfallswinkel jedes einzelnen Lichtstrahls ist mit i und der Brechungswinkel mit r bezeichnet. Die vier gelben Lichtstrahlen haben alle einen Einfallswinkel (i), der niedrig genug ist, um die Grenzfläche zwischen den beiden Medien zu passieren. Die beiden roten Lichtstrahlen haben jedoch Einfallswinkel, die den kritischen Winkel (etwa 41 Grad) überschreiten und werden entweder in die Grenze zwischen den Medien oder zurück in das Medium mit hohem Brechungsindex reflektiert. Dieses Phänomen tritt auf, wenn der Brechungswinkel (Winkel r in Abbildung 4) gleich 90 Grad wird und sich das Snellsche Gesetz auf Folgendes reduziert:

wobei (q) jetzt als kritischer Winkel C bezeichnet wird. Wenn das Medium mit geringerem Brechungsindex Luft ist (n = 1,00), die Gleichung reduziert sich weiter auf:

Wie bereits erwähnt, ist ein weiteres wichtiges Merkmal der Lichtbrechung, dass die Wellenlänge des Lichts einen Einfluss auf die Menge der Brechung hat, die innerhalb eines Mediums auftritt. Tatsächlich ist der Betrag der Brechung, der stattfindet, umgekehrt proportional zur Wellenlänge des einfallenden Lichts. Somit wird sichtbares Licht kürzerer Wellenlänge in einem größeren Winkel gebrochen als Licht längerer Wellenlänge. Wenn also weißes Licht, das sich aus allen Farben des sichtbaren Spektrums zusammensetzt, durch ein Glasprisma geleitet wird, wird es in Abhängigkeit von den einzelnen Wellenlängen in seine Teilfarben dispergiert. Niederfrequentes sichtbares Licht (600 Nanometer und mehr) wird in einem kleineren Winkel gebrochen als höherfrequentes Licht, was zu einem regenbogenartigen Effekt führt, wie unten in Abbildung 5 dargestellt.

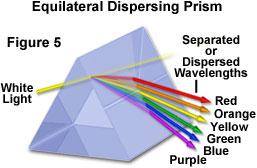
Dieses Phänomen ist auch für chromatische Aberration verantwortlich. Wenn weißes Licht durch eine einfache Konvexlinse geleitet wird, entstehen mehrere Brennpunkte in unmittelbarer Nähe, die den geringen Brechungsindexunterschieden der Komponentenwellenlängen entsprechen. Dieser Effekt neigt dazu, farbige (je nach Fokus entweder rot oder blau) Lichthöfe zu erzeugen, die die Bilder von Objekten umgeben. Die Korrektur dieser Aberration wird üblicherweise durch die Verwendung von Kombinationen von zwei oder mehr Linsenelementen erreicht, die aus Materialien mit unterschiedlichen dispersiven Eigenschaften bestehen, wie beispielsweise eine achromatische Linse, die sowohl mit Kronen- als auch mit Feuersteingläsern aufgebaut ist.

	Interactive Java Tutorial
Brechung durch ein Prisma Untersuchen Sie, wie weißes Licht durch Brechung durch verschiedene Winkel in einem Prisma in seine Komponentenfarben getrennt wird.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. Das gebräuchlichste Beispiel ist eine Kamera, die scharfe und fokussierte Bilder auf eine Filmemulsion oder die Oberfläche eines ladungsgekoppelten Bauelements (CCD) erzeugt, um ein genaues Bild zu erzeugen. Andere optische Geräte, die diese Eigenschaften des Lichts ausnutzen, umfassen Mikroskope und Teleskope, die die Betrachtung von Objekten ermöglichen, die für das bloße menschliche Auge unsichtbar sind, unabhängig davon, ob sie sich auf dem Kopf eines Stifts oder in einer entfernten Galaxie befinden.

Beitragende Autoren

Mortimer Abramowitz – Olympus America, Inc., Zwei Corporate Center-Laufwerk., Melville, New York, 11747.Shannon H. Neaves und Michael W. Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Die Florida State Universität, Tallahassee, Florida, 32310.

ZURÜCK ZU LICHT UND FARBE

Fragen oder Anmerkungen? Senden Sie uns eine E-Mail.

© 1998-2021 von Michael W. Davidson und der Florida State University. Alle Rechte vorbehalten. Keine Bilder, Grafiken, Skripte oder Applets dürfen ohne Genehmigung der Urheberrechtsinhaber reproduziert oder in irgendeiner Weise verwendet werden. Durch die Nutzung dieser Website erklären Sie sich mit allen von den Eigentümern festgelegten rechtlichen Bedingungen einverstanden.

Diese Website wird von unserem
Graphics & Webprogrammierteam
in Zusammenarbeit mit Optical Microscopy am
National High Magnetic Field Laboratory gepflegt.

Letzte Änderung: Freitag, 13.November 2015 um 02:18 Uhr

Zugriffszahl seit 10.März 2003:181405

Besuchen Sie die Webseiten unserer Partner im Bildungsbereich: