Phonon
Die Gleichungen in diesem Abschnitt verwenden keine Axiome der Quantenmechanik, sondern Beziehungen, für die es eine direkte Entsprechung in der klassischen Mechanik gibt.
Zum Beispiel: Ein starres regelmäßiges, kristallines (nicht amorphes) Gitter besteht aus N Teilchen. Diese Teilchen können Atome oder Moleküle sein. N ist eine große Zahl, z. B. in der Größenordnung von 1023 oder in der Größenordnung der Avogadro-Zahl für eine typische Probe eines Feststoffs. Da das Gitter starr ist, müssen die Atome Kräfte aufeinander ausüben, um jedes Atom in der Nähe seiner Gleichgewichtsposition zu halten. Diese Kräfte können Van-der-Waals-Kräfte, kovalente Bindungen, elektrostatische Anziehungen und andere sein, die alle letztendlich auf die elektrische Kraft zurückzuführen sind. Magnetische und Gravitationskräfte sind im Allgemeinen vernachlässigbar. Die Kräfte zwischen jedem Atompaar können durch eine potentielle Energiefunktion V charakterisiert werden, die vom Abstand der Trennung der Atome abhängt. Die potentielle Energie des gesamten Gitters ist die Summe aller paarweisen potentiellen Energien, multipliziert mit dem Faktor 1/2, um die Doppelzählung auszugleichen:
1 2 ∑ i ≠ j V (r i − r j ) {\displaystyle {\frac {1}{2}}\Summe _{i\neq j}V\links(r_{i}-r_{j}\rechts)}

wobei ri die Position des i-ten Atoms und V die potentielle Energie zwischen zwei Atomen ist.
Es ist schwierig, dieses Vielteilchenproblem explizit in der klassischen oder in der Quantenmechanik zu lösen. Um die Aufgabe zu vereinfachen, werden normalerweise zwei wichtige Annäherungen auferlegt. Erstens wird die Summe nur über benachbarte Atome durchgeführt. Obwohl sich die elektrischen Kräfte in realen Festkörpern bis ins Unendliche erstrecken, ist diese Annäherung immer noch gültig, da die von entfernten Atomen erzeugten Felder effektiv abgeschirmt werden. Zweitens werden die Potentiale V als harmonische Potentiale behandelt. Dies ist zulässig, solange die Atome nahe an ihren Gleichgewichtspositionen bleiben. Formal wird dies erreicht, indem Taylor V um seinen Gleichgewichtswert zur quadratischen Ordnung erweitert, wobei V proportional zur Verschiebung x2 und die elastische Kraft einfach proportional zu x ist. Der Fehler beim Ignorieren von Termen höherer Ordnung bleibt klein, wenn x nahe der Gleichgewichtsposition bleibt.
Das resultierende Gitter kann als ein System von Kugeln visualisiert werden, die durch Federn verbunden sind. Die folgende Abbildung zeigt ein kubisches Gitter, das ein gutes Modell für viele Arten von kristallinen Feststoffen darstellt. Andere Gitter umfassen eine lineare Kette, ein sehr einfaches Gitter, das wir in Kürze zur Modellierung von Phononen verwenden werden. (Für andere übliche Gitter siehe Kristallstruktur.)

Die potentielle Energie des Gitters kann nun als
∑ { i j } ( n n ) 1 2 n n ω 2 ( R i − R j ) 2 geschrieben werden. {\displaystyle \Summe _{\{ij\}(\mathrm {nn} )}{\tfrac {1}{2}}nn\omega ^{2}\links(R_{i}-R_{j}\rechts)^{2}.}

Hier ist ω die Eigenfrequenz der harmonischen Potentiale, die als gleich angenommen werden, da das Gitter regelmäßig ist. Ri ist die Positionskoordinate des i-ten Atoms, die wir jetzt von seiner Gleichgewichtsposition aus messen. Die Summe der nächsten Nachbarn wird als (nn) bezeichnet.
Lattice wavesEdit
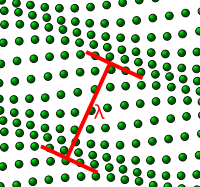
Aufgrund der Verbindungen zwischen Atomen führt die Verschiebung eines oder mehrerer Atome aus ihren Gleichgewichtspositionen zu einer Menge von Schwingungswellen, die sich durch das Gitter ausbreiten. Eine solche Welle ist in der Abbildung rechts dargestellt. Die Amplitude der Welle ist durch die Verschiebungen der Atome aus ihren Gleichgewichtspositionen gegeben. Die Wellenlänge λ ist markiert.
Es gibt eine minimal mögliche Wellenlänge, die durch den doppelten Gleichgewichtsabstand a zwischen Atomen gegeben ist. Jede Wellenlänge, die kürzer ist, kann aufgrund der Periodizität des Gitters auf eine Wellenlänge abgebildet werden, die länger als 2a ist. Dies kann als eine Konsequenz des Nyquist–Shannon-Abtasttheorems angesehen werden, die Gitterpunkte werden als „Abtastpunkte“ einer kontinuierlichen Welle angesehen.
Nicht jede mögliche Gitterschwingung hat eine genau definierte Wellenlänge und Frequenz. Die normalen Moden besitzen jedoch genau definierte Wellenlängen und Frequenzen.
Eindimensionales Gitterbearbeiten

Um die Analyse zu vereinfachen, die für ein 3-dimensionales Atomgitter erforderlich ist, ist es zweckmäßig, ein 1-dimensionales Gitter oder eine lineare Kette zu modellieren. Dieses Modell ist komplex genug, um die wichtigsten Merkmale von Phononen anzuzeigen.
Klassische Behandlungbearbeiten
Die Kräfte zwischen den Atomen werden als linear und benachbart angenommen und durch eine elastische Feder dargestellt. Jedes Atom wird als Punktteilchen angenommen und der Kern und die Elektronen bewegen sich im Schritt (adiabatischer Satz):
n − 1 n n + 1 ← a →
···o++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++o···
→→ → → →→ un − 1 un un + 1
wobei n das n-te Atom von insgesamt N ist, ist a der Abstand zwischen atome, wenn die Kette im Gleichgewicht ist, und nach der Verschiebung des n-ten Atoms aus seiner Gleichgewichtsposition.
Wenn C die elastische Konstante der Feder und m die Masse des Atoms ist, dann ist die Bewegungsgleichung des n−ten Atoms
− 2 C u n + C ( u n + 1 + u n – 1 ) = m d 2 u n d t 2 . {\displaystyle -2Cu_{n}+C\links(u_{n+1}+u_{n-1}\rechts)=m{\frac {d^{2}u_{n}}{dt^{2}}}.}

Dies ist ein Satz gekoppelter Gleichungen.
Da erwartet wird, dass die Lösungen oszillatorisch sind, werden neue Koordinaten durch eine diskrete Fourier-Transformation definiert, um sie zu entkoppeln.
Setzen Sie
u n = ∑ N a k / 2 π = 1 N Q k e i k n a. {\displaystyle u_{n}=\Summe _{Nak/2\pi =1}^{N}Q_{k}e^{ikna}.}

Hier entspricht na der stetigen Variablen x der Skalarfeldtheorie. Die Qk sind als Normalkoordinaten, Kontinuumsfeld und φk bekannt.
Die Substitution in die Bewegungsgleichung erzeugt die folgenden entkoppelten Gleichungen (dies erfordert eine signifikante Manipulation unter Verwendung der Orthonormalitäts− und Vollständigkeitsbeziehungen der diskreten Fourier-Transformation,
2 C (cos k a – 1) Q k = m d 2 Q k d t 2 . {\displaystyle 2C(\cos {ka-1})Q_{k}=m{\frac {d^{2}Q_{k}}{dt^{2}}}.}

Dies sind die Gleichungen für entkoppelte harmonische Oszillatoren mit der Lösung Q k = A k e i ω k t ; ω k = 2 C m (1 − cos k a). {\displaystyle Q_{k}=A_{k}e^{i\omega _{k}t};\qquad \omega _{k}={\sqrt {{\frac {2C}{m}}(1-\cos {ka})}}.}

Jede Normalkoordinate Qk repräsentiert einen unabhängigen Schwingungsmodus des Gitters mit der Wellenzahl k, der als Normalmodus bezeichnet wird.
Die zweite Gleichung für wk ist als Dispersionsrelation zwischen der Winkelfrequenz und der Wellenzahl bekannt.
In der Kontinuumsgrenze a→0, N→∞, wobei Na fest gehalten wird, un → φ(x), ein skalares Feld und ω ( k ) ∝ k a {\displaystyle \omega (k)\propto ka}

. Dies entspricht der klassischen Theorie des freien skalaren Feldes, einer Anordnung unabhängiger Oszillatoren.
Quantenbehandlungbearbeiten
Eine eindimensionale quantenmechanische harmonische Kette besteht aus N identischen Atomen. Dies ist das einfachste quantenmechanische Modell eines Gitters, aus dem Phononen entstehen können. Der Formalismus für dieses Modell lässt sich leicht auf zwei und drei Dimensionen verallgemeinern.
Im Gegensatz zum vorherigen Abschnitt werden die Positionen der Massen nicht mit ui bezeichnet, sondern mit x1, x2…, gemessen von ihren Gleichgewichtspositionen (d.h. xi = 0, wenn sich das Teilchen i in seiner Gleichgewichtsposition befindet.) In zwei oder mehr Dimensionen sind die xi Vektorgrößen. Der Hamiltonian für dieses System ist
H = ∑ i = 1 N p i 2 2 m + 1 2 m ω 2 ∑ {i j } ( n n ) (x i − x j ) 2 {\displaystyle {\mathcal {H}}=\Summe _{i=1}^{N}{\frac {p_{i}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}\Summe _{\{ij\}(\mathrm {nn} )}\left(x_{i}-x_{j}\right)^{2}}

wobei m die Masse jedes Atoms ist (vorausgesetzt, es ist für alle gleich) und xi und pi die Positions- bzw. Impulsoperatoren sind, für das i-te Atom und die Summe wird über die nächsten Nachbarn (nn) gemacht. Man erwartet jedoch, dass in einem Gitter auch Wellen auftreten können, die sich wie Teilchen verhalten. Es ist üblich, mit Wellen im Fourierraum umzugehen, der anstelle von Koordinaten von Teilchen normale Moden des Wellenvektors als Variablen verwendet. Die Anzahl der normalen Modi entspricht der Anzahl der Partikel. Der Fourierraum ist jedoch angesichts der Periodizität des Systems sehr nützlich.
Es kann ein Satz von N „Normalkoordinaten“ Qk eingeführt werden, definiert als die diskreten Fourier−Transformationen der xk und N „konjugierte Momente“ Πk definiert als die Fourier-Transformationen der pk:
Q k = 1 N ∑ l e i k a l x l Π k = 1 N ∑ l e – i k a l p l. {\displaystyle {\begin{n}Q_{k}&={\frac {1}{\sqrt {N}}}\Summe _{l}e^{ikal}x_{l}\\\Pi _{k}&={\frac {1}{\sqrt {N}}}\summe _{l}e^ {-ikal}p_{l}.\end{aligned}}}

Die Größe kn entpuppt sich als die Wellenzahl des Phonons, d.h. 2π geteilt durch die Wellenlänge.
Diese Wahl behält die gewünschten Kommutierungsbeziehungen entweder im realen Raum oder im Wellenvektorraum bei
= i ℏ δ l , m = 1 N ∑ l , m e i k a l e − i k ‚ a m = i ℏ N ∑ l e i a l ( k − k ‚ ) = i ℏ δ k , k ‚ = = 0 {\displaystyle {\begin{aligned}\left&=i\hbar \delta _{l,m links&={\frac {1}{N}}\Summe _{l, m} e^{ikal}e^{-ik’am}\links\\&={\frac {i\hbar }{N}}\summe _{l} e^{ial\links (k-k’\rechts)}=i\ hbar \delta _{k,k‘}\\\links&=\links=0\Ende{ausgerichtet}}}

Aus dem Allgemeinen Ergebnis
∑ l x l x l + m = 1 N ∑ k k Q k Q k ‚∑ l e i a l ( k + k ‚ ) e i a m k ‚ = ∑ k F k F − k e i m k ∑ l p l 2 = ∑ k Π k Π k {\displaystyle {\begin{aligned}\sum _{l}x_{l}x_{l+m}&={\frac {1}{N}}\sum _{kk‘}Q_{k}Q_{k‘}\sum _{l}e^{ial\left(k+k’\right)}e^{iamk‘}=\sum _{k}Q_{k}Q_{-k}e^{iamk}\\\Summe _{l}{p_{l}}^{2}&=\Summe _{k}\Pi _{k}\Pi _{-k}\Ende{ausgerichtet}}}
 1 2 m ω 2 ∑ j ( x j – x j + 1 ) 2 = 1 2 m ω 2 ∑ k Q k Q − k (2 − e i k − e − i q ) = 1 2 ∑ k I ω k 2 Q k − Q k {\displaystyle {\tfrac {1}{2}}m\omega ^{2}\sum _{j}\links(x_{j}-x_{j+1}\rechts)^{2}={\tfrac {1}{2}}m\omega ^{2}\Summe _{k}Q_{k}Q_{-k}(2-e^{ika}-e^{-ika})={\tfrac {1}{2}}\Summe _{k}m{\omega _{k}}^{2}Q_{k}Q_{-k}}
1 2 m ω 2 ∑ j ( x j – x j + 1 ) 2 = 1 2 m ω 2 ∑ k Q k Q − k (2 − e i k − e − i q ) = 1 2 ∑ k I ω k 2 Q k − Q k {\displaystyle {\tfrac {1}{2}}m\omega ^{2}\sum _{j}\links(x_{j}-x_{j+1}\rechts)^{2}={\tfrac {1}{2}}m\omega ^{2}\Summe _{k}Q_{k}Q_{-k}(2-e^{ika}-e^{-ika})={\tfrac {1}{2}}\Summe _{k}m{\omega _{k}}^{2}Q_{k}Q_{-k}}

wobei
ω k = 2 ω 2 (1 − cos (k a ) = 2 ω | sin k 2 | {\displaystyle \omega _{k}={\sqrt {2\omega ^{2}\links(1-\cos {ka}\rechts)}}=2\ omega \links |\sin {\frac {ka}{2}}\rechts|}

Der Hamiltonian kann in den Wellenvektorraum geschrieben werden als
H = 1 2 m ∑ k ( Π k Π − k + m 2 ω k 2 Q k Q − k ) {\displaystyle {\mathcal {H}}={\frac {1}{2m}}\Summe _{k}\links(\Pi _{k}\Pi _{-k}+m^{2}\omega _{k}^{2}Q_{k}Q_{-k}\rechts)}

Die Kopplungen zwischen den Positionsvariablen wenn Q und Π hermitianisch wären (was sie nicht sind), würde der transformierte Hamiltonian N entkoppelte harmonische Oszillatoren beschreiben.
Die Form der Quantisierung hängt von der Wahl der Randbedingungen ab; der Einfachheit halber werden periodische Randbedingungen auferlegt, die das (N + 1) -te Atom als äquivalent zum ersten Atom definieren. Physikalisch entspricht dies dem Verbinden der Kette an ihren Enden. Die resultierende Quantisierung ist
k = k n = 2 π n N a für n = 0 , ± 1 , ± 2 , … ± N 2 . {\displaystyle k=k_{n}={\frac {2\pi n}{Na}}\quad {\mbox{für }}n=0,\pm 1,\pm 2,\ldots \pm {\frac {N}{2}}.\ }

Die obere Grenze zu n ergibt sich aus der minimalen Wellenlänge, die doppelt so groß ist wie der Gitterabstand a, wie oben diskutiert.
Die harmonischen Oszillatoreigenwerte bzw. Energieniveaus für den Modus wk sind:
E n = ( 1 2 + n ) ℏ ω k n = 0 , 1 , 2 , 3 … {\ displaystyle E_{n}=\links({\tfrac {1}{2}}+n\rechts)\hbar \omega _{k}\qquad n=0,1,2,3\ldots }

Die Ebenen sind gleichmäßig:
1 2 ℏ ω , 3 2 ℏ ω , 5 2 ℏ ω ⋯ {\displaystyle {\tfrac {1}{2}}\hbar \omega ,\ {\tfrac {3}{2}}\hbar \omega ,\ {\tfrac {5}{2}}\hbar \omega \ \cdots }

wobei 1/2ħw die Nullpunktsenergie eines quantenharmonischen Oszillators ist.
Dem harmonischen Oszillatorgitter muss eine genaue Energiemenge ħ w zugeführt werden, um es auf das nächste Energieniveau zu bringen. Im Vergleich zum Photonenfall, wenn das elektromagnetische Feld quantisiert wird, wird das Quantum der Schwingungsenergie als Phonon bezeichnet.
Alle Quantensysteme zeigen gleichzeitig wellen- und teilchenähnliche Eigenschaften. Die teilchenähnlichen Eigenschaften des Phonons lassen sich am besten mit den später beschriebenen Methoden der zweiten Quantisierung und Operatortechniken verstehen.
Dreidimensionales Gitterbearbeiten
Dies kann auf ein dreidimensionales Gitter verallgemeinert werden. Die Wellenzahl k wird durch einen dreidimensionalen Wellenvektor k ersetzt. Weiterhin ist nun jedem k drei Normalkoordinaten zugeordnet.
Die neuen Indizes s = 1, 2, 3 kennzeichnen die Polarisation der Phononen. Im eindimensionalen Modell waren die Atome darauf beschränkt, sich entlang der Linie zu bewegen, so dass die Phononen Longitudinalwellen entsprachen. In drei Dimensionen ist die Schwingung nicht auf die Ausbreitungsrichtung beschränkt und kann auch in den senkrechten Ebenen auftreten, wie transversale Wellen. Dies führt zu den zusätzlichen normalen Koordinaten, die, wie die Form des Hamiltonian zeigt, können wir als unabhängige Arten von Phononen.
Dispersion relationEdit

Für eine eindimensionale alternierende Anordnung von zwei Arten von Ionen oder Atomen der Masse m1, m2, die periodisch in einem Abstand a wiederholt werden und durch Federn der Federkonstante K verbunden sind, ergeben sich zwei Vibrationsmodi:
ω ± 2 = K (1 m 1 + 1 m 2 ) ± K (1 m 1 + 1 m 2 ) 2 − 4 sin 2 k a 2 m 1 m 2 , {\displaystyle \omega _{\pm }^{2}=K\links({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\rechts)\pm K{\sqrt {\links({\frac {1}{m_{1}}}+{ \frac {1}{m_{2}}}\rechts)^{2}-{\frac {4\sin ^{2}{\frac {ka}{2}}}{m_{1}m_{2}}}}},}

wobei k der Wellenvektor der Schwingung ist, der sich auf seine wellenlänge durch k = 2 π λ {\displaystyle k={\tfrac {2\pi }{\lambda }}}

.
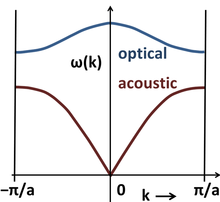
Die Verbindung zwischen Frequenz und Wellenvektor, ω = ω(k), wird als Dispersionsrelation bezeichnet. Das Pluszeichen ergibt den sogenannten optischen Modus und das Minuszeichen den akustischen Modus. Im optischen Modus bewegen sich zwei benachbarte verschiedene Atome gegeneinander, während sie sich im akustischen Modus zusammen bewegen.
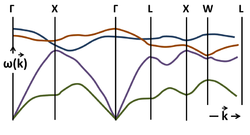
Die Ausbreitungsgeschwindigkeit eines akustischen Phonons, die auch die Schallgeschwindigkeit im Gitter ist, ist durch die Steigung der akustischen Dispersionsrelation ∂wk/∂k gegeben (siehe Gruppengeschwindigkeit.) Bei niedrigen Werten von k (d. h. langen Wellenlängen) ist die Dispersionsbeziehung nahezu linear und die Schallgeschwindigkeit ist unabhängig von der Phononenfrequenz ungefähr wa. Infolgedessen können sich Pakete von Phononen mit unterschiedlichen (aber langen) Wellenlängen über große Entfernungen über das Gitter ausbreiten, ohne auseinanderzubrechen. Dies ist der Grund, warum sich Schall ohne signifikante Verzerrung durch Festkörper ausbreitet. Dieses Verhalten scheitert bei großen Werten von k, also kurzen Wellenlängen, an den mikroskopischen Details des Gitters.Für einen Kristall, der mindestens zwei Atome in seiner primitiven Zelle hat, weisen die Dispersionsbeziehungen zwei Arten von Phononen auf, nämlich optische und akustische Moden, die der oberen blauen bzw. unteren roten Kurve im Diagramm entsprechen. Die vertikale Achse ist die Energie oder Frequenz des Phonons, während die horizontale Achse der Wellenvektor ist. Die Grenzen bei −π/a und π/a sind die der ersten Brillouin-Zone. Ein Kristall mit N ≥ 2 verschiedenen Atomen in der primitiven Zelle weist drei akustische Modi auf: einen longitudinalen akustischen Modus und zwei transversale akustische Modi. Die Anzahl der optischen Modi beträgt 3N – 3. Die untere Abbildung zeigt die Dispersionsbeziehungen für mehrere Phononenmoden in GaAs als Funktion des Wellenvektors k in den Hauptrichtungen seiner Brillouin-Zone.
Viele Phononendispersionskurven wurden durch inelastische Neutronenstreuung gemessen.Die Physik des Schalls in Flüssigkeiten unterscheidet sich von der Physik des Schalls in Festkörpern, obwohl beide Dichtewellen sind: Schallwellen in Flüssigkeiten haben nur longitudinale Komponenten, während Schallwellen in Festkörpern longitudinale und transversale Komponenten haben. Dies liegt daran, dass Flüssigkeiten keine Scherspannungen unterstützen können (siehe jedoch viskoelastische Flüssigkeiten, die nur für hohe Frequenzen gelten).
Interpretation von Phononen mit zweiten Quantisierungstechnikenbearbeiten
Der oben abgeleitete Hamiltonian mag wie eine klassische Hamiltonian-Funktion aussehen, aber wenn er als Operator interpretiert wird, beschreibt er eine Quantenfeldtheorie nicht wechselwirkender Bosonen.Die zweite Quantisierungstechnik, ähnlich der Leiteroperatormethode, die für quantenharmonische Oszillatoren verwendet wird, ist ein Mittel zum Extrahieren von Energieeigenwerten, ohne die Differentialgleichungen direkt zu lösen. Gegeben ist der Hamiltonian, H {\displaystyle {\mathcal {H}}}

, sowie die konjugierte Position, Q k {\displaystyle Q_{k}}

, und der konjugierte Impuls Π k {\displaystyle \ Pi _{k}}

Definiert im obigen Abschnitt zur Quantenbehandlung können wir Erschaffungs- und Vernichtungsoperatoren definieren: b k = Ich ω k 2 ℏ ( Q k + ich m ω k Π − k ) {\displaystyle b_{k}={\sqrt {\frac {m\omega _{k}}{2\hbar }}}\links(Q_{k}+{\frac {i}{m\omega _{k}}}\Pi _{-k}\rechts)}

und b k † = I ω k 2 ℏ ( Q − k − i I ω k Π k ) {\displaystyle {b_{k}}^{\dolch }={\sqrt {\frac {m\omega _{k}}{2\ hbar }}}\links(Q_{-k}-{\frac {i}{m\omega _{k}}}\Pi _{k}\rechts)}

Die folgenden Kommutatoren können leicht durch Substitution in der kanonischen Kommutierungsrelation erhalten werden:
= δ k , k ‚ , = = 0 {\displaystyle \left=\delta _{k,k‘},\quad {\Big }=\left=0}

Auf diese Weise können die Operatoren bk† und bk invertiert werden, um die konjugierte Position und den Impuls als:
Q k = ℏ 2 m ω k (b k † + b − k ) {\displaystyle Q_{k}={\sqrt {\frac {\hbar }{2m\omega _{k}}}}\links({b_{k}}^{\dolch }+b_{-k}\rechts)}

und Π k = i ℏ m ω k 2 (b k † − b − k ) {\displaystyle \Pi _{k}=i{\sqrt {\frac {\hbar m\omega _{k}}{2}}}\links({b_{k}}^{\ k}\rechts)}

ersetzen dieser Definitionen für Q k {\displaystyle Q_{k}}

und Π k {\displaystyle \Pi _{k}}

in den hamiltonschen Wellenvektorraum, wie er oben definiert ist, und Vereinfachen führt dann zu der Hamiltonian in der Form: H = ∑ k ℏ ω k (b k † b k + 1 2 ) {\displaystyle {\mathcal {H}}=\Summe _{k}\hbar \omega _{k}\links({b_{k}}^{\dolch }b_{k}+{\tfrac {1}{2}}\rechts)}

Dies wird als zweite Quantisierungstechnik bezeichnet, die auch als occupation number formulation bezeichnet wird, wobei nk = bk†bk die occupation number ist. Dies kann als eine Summe von N unabhängigen Oszillator-Hamiltonianern mit jeweils einem eindeutigen Wellenvektor angesehen werden und ist kompatibel mit den Methoden, die für den quantenharmonischen Oszillator verwendet werden (beachten Sie, dass nk hermitian ist). Wenn ein Hamiltonian als eine Summe von pendelnden Sub-Hamiltonians geschrieben werden kann, werden die Energieeigenzustände durch die Produkte von Eigenzuständen von jedem der getrennten Sub-Hamiltonians gegeben. Das entsprechende Energiespektrum ergibt sich dann aus der Summe der einzelnen Eigenwerte der Sub-Hamiltonianer.
Wie beim quantenharmonischen Oszillator kann man zeigen, dass bk† bzw. bk eine einzelne Felderregung, ein Phonon, mit einer Energie von ħwk erzeugen und zerstören.
Aus dieser Technik lassen sich drei wichtige Eigenschaften von Phononen ableiten. Erstens sind Phononen Bosonen, da durch wiederholte Anwendung des Erstellungsoperators bk† beliebig viele identische Anregungen erzeugt werden können. Zweitens ist jedes Phonon ein „kollektiver Modus“, der durch die Bewegung jedes Atoms im Gitter verursacht wird. Dies ergibt sich aus der Tatsache, dass die hier im Impulsraum definierten Erstellungs- und Vernichtungsoperatoren Summen über die Positions- und Impulsoperatoren jedes Atoms enthalten, wenn sie in den Positionsraum geschrieben werden (siehe Positions- und Impulsraum). Schließlich kann unter Verwendung der Position–Position-Korrelationsfunktion gezeigt werden, dass Phononen als Wellen der Gitterverschiebung wirken.
Diese Technik lässt sich leicht auf drei Dimensionen verallgemeinern, wobei der Hamiltonian die Form annimmt:
H = ∑ k ∑ s = 1 3 ℏ ω k , s ( b k , s † b k , s + 1 2 ) . {\displaystyle {\mathcal {H}}=\Summe _{k}\Summe _{s=1}^{3}\hbar \,\omega _{k,s}\links({b_{k,s}}^{\Dolch }b_{k,s}+{\tfrac {1}{2}}\rechts).}
