Prealgebra
Lernergebnisse
- Finden Sie die Fläche, Basis und Höhe eines Dreiecks
- Finden Sie die Länge einer Seite eines Dreiecks angesichts des Umfangs und zwei anderer Längen
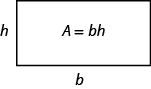
Wir wissen jetzt, wie man die Fläche eines Rechtecks findet. Wir können diese Tatsache verwenden, um die Formel für die Fläche eines Dreiecks zu visualisieren. Im Rechteck unten haben wir die Länge b und die Breite h beschriftet, sodass die Fläche bh ist.
Die Fläche eines Rechtecks ist die Basis, b, mal die Höhe, h.
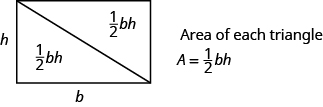
Wir können dieses Rechteck in zwei kongruente Dreiecke teilen (siehe Bild unten). Dreiecke, die kongruent sind, haben identische Seitenlängen und Winkel, und so sind ihre Flächen gleich. Die Fläche jedes Dreiecks ist die Hälfte der Fläche des Rechtecks oder \frac{1}{2}bh. Dieses Beispiel hilft uns zu verstehen, warum die Formel für die Fläche eines Dreiecks A=\frac{1}{2}bh ist.
Ein Rechteck kann in zwei gleich große Dreiecke geteilt werden. Die Fläche jedes Dreiecks ist die Hälfte der Fläche des Rechtecks.
Die Formel für die Fläche eines Dreiecks lautet A=\frac{1}{2}bh, wobei b die Basis und h die Höhe ist.
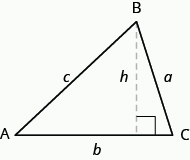
Um die Fläche des Dreiecks zu finden, müssen Sie seine Basis und Höhe kennen. Die Basis ist die Länge einer Seite des Dreiecks, normalerweise die Seite unten. Die Höhe ist die Länge der Linie, die die Basis mit dem gegenüberliegenden Scheitelpunkt verbindet und einen \text{90} ^ \circ Winkel mit der Basis bildet. Das Bild unten zeigt drei Dreiecke mit der Basis und Höhe jedes markierten.
Die Höhe h eines Dreiecks ist die Länge eines Liniensegments, das die Basis mit dem gegenüberliegenden Scheitelpunkt verbindet und einen \text{90}^ \circ Winkel mit der Basis bildet.

Dreieckseigenschaften
Für jedes Dreieck \Delta ABC ist die Summe der Winkelmaße \text{180}^ \circ.
m\angle{A}+m\angle{B}+m\angle{C}=180^\circ
Der Umfang eines Dreiecks ist die Summe der Längen der Seiten.
P=a+b+c
Die Fläche eines Dreiecks ist die Hälfte der Basis, b, mal der Höhe, h.
A=\frac{1}{2}bh
Beispiel
Ermitteln Sie die Fläche eines Dreiecks, dessen Basis 11 Zoll und dessen Höhe 8 Zoll beträgt.
Lösung
| Schritt 1. Lesen Sie das Problem. Zeichnen Sie die Figur und beschriften Sie sie mit den angegebenen Informationen. |  |
| Schritt 2. Identifizieren Sie, wonach Sie suchen. | die Fläche des Dreiecks |
| Schritt 3. Name. Wählen Sie eine Variable aus, um sie darzustellen. | sei A = Fläche des Dreiecks |
| Schritt 4.Übersetzen.
Schreiben Sie die entsprechende Formel. Ersetzen. |
 |
| Schritt 5. Löse die Gleichung. | A=44 Quadratzoll. |
| Schritt 6. Überprüfen Sie:
A=\frac{1}{2}bh 44\stackrel{?}{=}\frac{1}{2}(11)8 44=44\Häkchen setzen |
|
| Schritt 7. Beantworte die Frage. | Die Fläche beträgt 44 Quadratzoll. |
probieren Sie es aus
Beispiel
Der Umfang eines dreieckigen Gartens beträgt 24 Fuß. Die Längen von zwei Seiten sind 4 Fuß und 9 Fuß. Wie lang ist die dritte Seite?
probieren Sie es aus
Beispiel
Die Fläche eines dreieckigen Kirchenfensters beträgt 90 Quadratmeter. Die Basis des Fensters ist 15 Meter. Was ist die Höhe des Fensters?
probieren Sie es aus
Gleichschenklige und gleichseitige Dreiecke
Neben dem rechtwinkligen Dreieck haben einige andere Dreiecke spezielle Namen. Ein Dreieck mit zwei gleich langen Seiten wird als gleichschenkliges Dreieck bezeichnet. Ein Dreieck mit drei Seiten gleicher Länge wird als gleichseitiges Dreieck bezeichnet. Das Bild unten zeigt beide Arten von Dreiecken.
In einem gleichschenkligen Dreieck haben zwei Seiten die gleiche Länge und die dritte Seite ist die Basis. In einem gleichseitigen Dreieck haben alle drei Seiten die gleiche Länge.
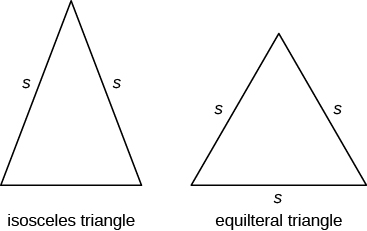
Gleichschenklige und gleichseitige Dreiecke
Ein gleichschenkliges Dreieck hat zwei Seiten gleicher Länge.
Ein gleichseitiges Dreieck hat drei Seiten gleicher Länge.
Beispiel
Der Umfang eines gleichseitigen Dreiecks beträgt 93 Zoll. Finden Sie die Länge jeder Seite.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. Der Schal wird ein gleichschenkliges Dreieck mit einer Basis von
60 Zoll sein. Wie lange kann sie die beiden gleichen Seiten machen?








