seaborn.histplot(Daten= Keine, *, x= Keine, y= Keine, Farbton = Keine, gewichte= Keine, stat=’count‘, bins=’auto‘, binwidth= Keine, binrange= Keine, diskrete = Keine, kumulative=Falsch, common_bins= True, common_norm=True, multiple=’layer‘, element=’bars‘, fill=True, shrink=1, kde=False, kde_kws=None, line_kws=None, thresh=0, pthresh=None, pmax=None, cbar=False, cbar_ax=None, cbar_kws=None, palette=None, hue_order=None, hue_norm=None, color=None, log_scale=None, legend=True, ax=None, **kwargs)¶

Plot univariate bivariate Histogramme zur Darstellung von DataSet.

Ein Histogramm ist ein klassisches Visualisierungstool, das die Verteilung einer oder mehrerer Variablen darstellt, indem die Anzahl der Beobachtungen gezählt wird, die in bestimmte Bins fallen.

Diese Funktion kann die in jedem Bin berechnete Statistik normalisieren, um die Frequenz, Dichte oder Wahrscheinlichkeitsmasse zu schätzen, und sie kann eine glatte Kurve hinzufügen, die mit einer Kerndichteschätzung erhalten wird, ähnlich wie kdeplot().

Weitere Informationen finden Sie im Benutzerhandbuch.

Parameter Datenpandas.DataFramenumpy.ndarray, Zuordnung oder Sequenz

Eingabedatenstruktur. Entweder eine Long-Form-Sammlung von Vektoren, die benannten Variablen zugewiesen werden können, oder ein Wide-Form-Dataset, das intern neu geformt wird.

x, yvektoren oder Schlüssel indata

Variablen, die Positionen auf der x- und y-Achse angeben.

huevector oder key indata

Semantische Variable, die zur Bestimmung der Farbe von Plotelementen zugeordnet wird.

weightsvector oder key indata

Wenn angegeben, gewichten Sie den Beitrag der entsprechenden Datenpunkte zur Zählung in jedem Bin mit diesen Faktoren.

stat{„count“, „frequency“, „density“, „probability“}

Aggregierte Statistik zur Berechnung in jedem Bin.

• count zeigt die Anzahl der Beobachtungen an

• frequency zeigt die Anzahl der Beobachtungen geteilt durch die Behälterbreite an

• density normalisiert die Zählungen so, dass der Bereich der histogramm ist 1

• probability normalisiert die Zählungen so, dass die Summe der Balkenhöhen 1 ist

binsstr, number, vector oder ein Paar solcher Werte

Generischer bin-Parameter, der der Name einer Referenzregel, die Anzahl der Bins oder die Anzahl der Bins sein kann.Übergeben an numpy.histogram_bin_edges().

binwidthnumber oder Zahlenpaar

Breite jedes Bin, überschreibt bins kann aber mitbinrange verwendet werden.

binrangepaar von Zahlen oder ein Paar von Paaren

Niedrigster und höchster Wert für Bin-Kanten; kann entweder mit bins oder binwidth verwendet werden. Standardmäßig Daten Extreme.

discretebool

Wenn True, setzen Sie standardmäßig binwidth=1 und zeichnen Sie die Balken so, dass sie auf den entsprechenden Datenpunkten zentriert sind. Dies vermeidet „Lücken“, die möglichandernfalls bei Verwendung diskreter (ganzzahliger) Daten auftreten.

cumulativebool

Wenn True, zeichnen Sie die kumulierten Zählungen als Bins erhöhen.

common_binsbool

Wenn True, verwenden Sie dieselben Bins, wenn semantische Variablen Multipleplots erzeugen. Wenn Sie eine Referenzregel verwenden, um die Bins zu bestimmen, wird sie mit dem vollständigen Datensatz berechnet.

common_normbool

Wenn True und eine normalisierte Statistik verwendet wird, wird die Normalisierung über den gesamten Datensatz angewendet. Andernfalls normalisieren Sie jedes Histogramm unabhängig voneinander.

multiple{„layer“, „dodge“, „stack“, „fill“}

Ansatz zur Auflösung mehrerer Elemente, wenn semantisches Mapping Teilmengen erstellt.Nur relevant bei univariaten Daten.

element{„bars“, „step“, „poly“}

Visuelle Darstellung der Histogrammstatistik.Nur relevant bei univariaten Daten.

fillbool

Wenn True, füllen Sie das Feld unter dem Histogramm aus.Nur relevant bei univariaten Daten.

shrinknumber

Skalieren Sie die Breite jedes Balkens relativ zur binwidth um diesen Faktor.Nur relevant bei univariaten Daten.

kdebool

Wenn True, berechnen Sie eine Schätzung der Kerndichte, um die Verteilung zu glätten und auf dem Plot als (eine oder mehrere) Linie(n) anzuzeigen.Nur relevant bei univariaten Daten.

kde_kwsdict

Parameter, die die KDE-Berechnung steuern, wie in kdeplot().

line_kwsdict

Parameter, die die KDE-Visualisierung steuern, übergeben anmatplotlib.axes.Axes.plot().

numbernumber oder None

Zellen mit einer Statistik kleiner oder gleich diesem Wert sind transparent.Nur relevant bei bivariaten Daten.

pthreshnumber oder None

Wie thresh , aber ein Wert, bei dem Zellen mit aggregierten Zählungen (oder anderen Statistiken, wenn verwendet) bis zu diesem Anteil an der Gesamtsumme sind transparent.

pmaxnumber oder None

Ein Wert, der diesen Sättigungspunkt für die Farbkarte auf einen Wert festlegt, so dass die Zellen darunter diesen Anteil an der Gesamtanzahl (oder eine andere Statistik, wenn verwendet) darstellen.

cbarbool

Wenn True, fügen Sie eine Farbleiste hinzu, um die Farbzuordnung in einem bivariaten Diagramm zu kommentieren.Hinweis: Unterstützt derzeit keine Diagramme mit einer hue Variablen well .

cbar_axmatplotlib.axes.Axes

Bereits vorhandene Achsen für die Farbleiste.

cbar_kwsdict

Zusätzliche Parameter an matplotlib.figure.Figure.colorbar() übergeben.

palettestring, list, dict odermatplotlib.colors.Colormap

Methode zur Auswahl der Farben, die beim Mappen der hue Semantik verwendet werden sollen.String-Werte werden an color_palette() übergeben. Liste oder Diktat valuesimply kategoriale Zuordnung, während ein colormap Objekt numerische Zuordnung impliziert.

hue_ordervector von Strings

Geben Sie die Reihenfolge der Verarbeitung und Plotten für kategoriale Ebenen derhue Semantik.

hue_normtuple odermatplotlib.colors.Normalize

Entweder ein Wertepaar, das den Normalisierungsbereich in Dateneinheiten festlegt, oder ein Objekt, das von Dateneinheiten in ein Intervall abgebildet wird. Verwendungimpliziert numerische Zuordnung.

colormatplotlib color

Einzelfarbspezifikation für den Fall, dass das Hue Mapping nicht verwendet wird. Andernfalls versucht theplot, sich in den matplotlib-Eigenschaftszyklus einzubinden.

log_scalebool or number, or pair of bools or numbers

Legen Sie eine Logskala auf der Datenachse (oder Achsen mit bivariaten Daten) mit der angegebenen Basis (Standard 10) fest und werten Sie das KDE im Lograum aus.

legendbool

Wenn False, unterdrücken Sie die Legende für semantische Variablen.

axmatplotlib.axes.Axes

Bereits vorhandene Achsen für den Plot. Andernfalls rufen Sie matplotlib.pyplot.gca()intern auf.

kwargs

Andere Schlüsselwortargumente werden an eine der folgenden matplotlibfunctions übergeben:

• matplotlib.axes.Axes.bar() (univariate, element=“bars“)

• matplotlib.axes.Axes.fill_between() (univariate, other element, fill=True)

• matplotlib.axes.Axes.plot() (univariate, other element, fill=False)

• matplotlib.axes.Axes.pcolormesh() (bivariate)

Returnsmatplotlib.axes.Axes

The matplotlib axes containing the plot.

Anmerkungen

Die Wahl der Bins für die Berechnung und das Zeichnen eines Histogramms kann einen wesentlichen Einfluss auf die Erkenntnisse haben, die man aus der Visualisierung ziehen kann. Wenn die Behälter zu groß sind, können sie wichtige Funktionen löschen.Auf der anderen Seite können zu kleine Bins von randomvariability dominiert werden, wodurch die Form der wahren zugrunde liegenden Verteilung verdeckt wird. Die Standard-Bin-Größe wird anhand einer Referenzregel bestimmt, die von der Stichprobengröße und der Varianz abhängt. Dies funktioniert in vielen Fällen gut (dh mit „gut erzogenen“ Daten), schlägt jedoch in anderen Fällen fehl. Es ist immer gut, verschiedene Behältergrößen auszuprobieren, um sicherzustellen, dass Sie nichts Wichtiges verpassen.Mit dieser Funktion können Sie Behälter auf verschiedene Arten angeben, z. B. durch Festlegen der Gesamtzahl der zu verwendenden Behälter, der Breite jedes Behälters oder der spezifischen Stellen, an denen die Behälter brechen sollen.

Beispiele

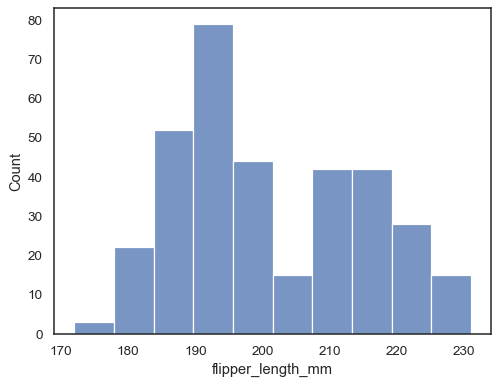
Weisen Sie xeine Variable zu, um eine univariate Verteilung entlang der x-Achse zu zeichnen:

penguins = sns.load_dataset("penguins")sns.histplot(data=penguins, x="flipper_length_mm")

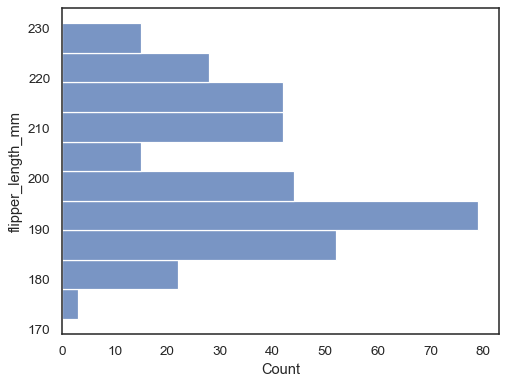
Drehen Sie den Plot um, indem Sie die Datenvariable der y-Achse zuweisen:

sns.histplot(data=penguins, y="flipper_length_mm")

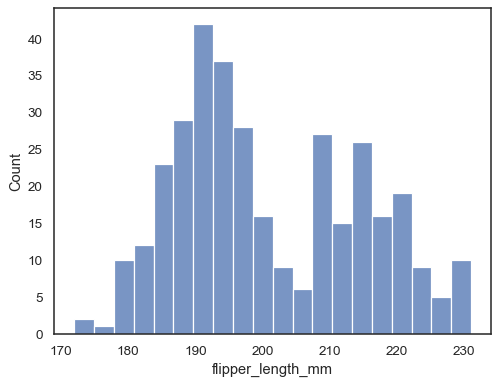
Überprüfen Sie, wie gut das Histogramm die Daten darstellt, indem Sie eine andere Bin-Breite angeben:

sns.histplot(data=penguins, x="flipper_length_mm", binwidth=3)

Sie können auch die Gesamtzahl der zu verwendenden Bins definieren:

sns.histplot(data=penguins, x="flipper_length_mm", bins=30)

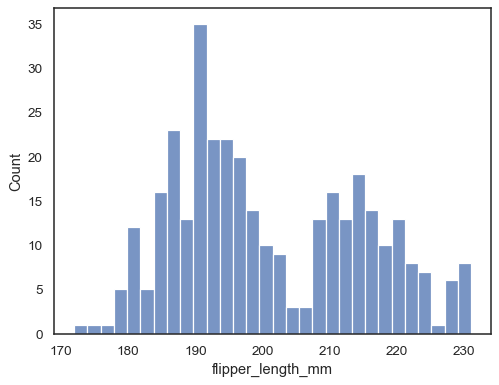
Fügen Sie eine Schätzung der Kerndichte hinzu, um das Histogramm zu glätten und zusätzliche Informationen über die Form der Verteilung bereitzustellen:

sns.histplot(data=penguins, x="flipper_length_mm", kde=True)

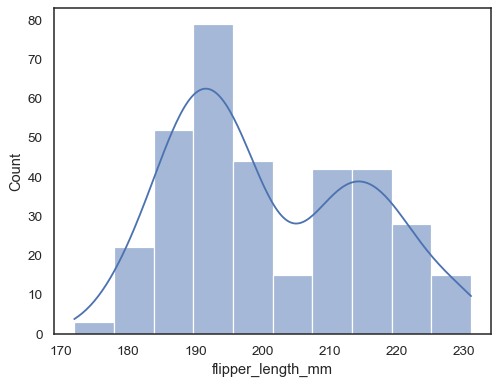
Wenn weder x noch y zugewiesen ist, wird der Datensatz als In-Form behandelt und für jede numerische Spalte ein Histogramm gezeichnet:

sns.histplot(data=penguins)

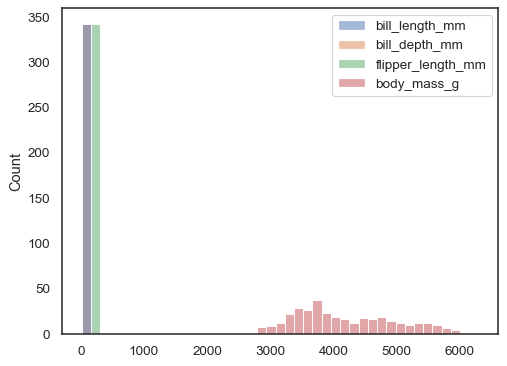
Sie können ansonsten mehrere Histogramme aus einem Langform-Datensatz mithue Mapping:

sns.histplot(data=penguins, x="flipper_length_mm", hue="species")

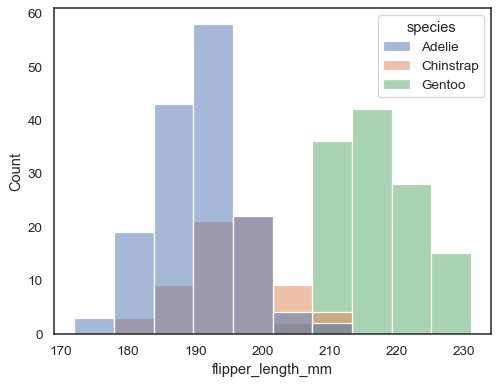
Der Standardansatz zum Zeichnen mehrerer Distributionen besteht darin, sie zu „schichten“, aber Sie können sie auch „stapeln:

sns.histplot(data=penguins, x="flipper_length_mm", hue="species", multiple="stack")

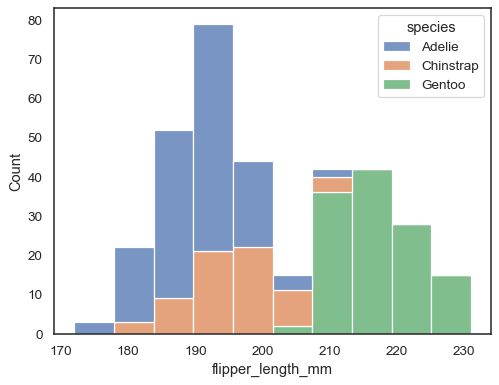
Überlappende Balken können schwer visuell aufzulösen sein. Ein anderer Ansatz wäre, eine Schrittfunktion zu zeichnen:

sns.histplot(penguins, x="flipper_length_mm", hue="species", element="step")

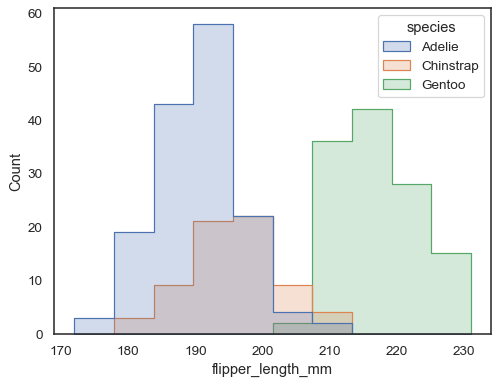
Sie können sich noch weiter von Balken entfernen, indem Sie ein Polygon mit zeichnen Ecken in der Mitte jedes Behälters. Dies kann es einfacher machen, die Form der Verteilung zu sehen, aber mit Vorsicht verwenden: Es wird weniger offensichtlich sein, dass Ihr Publikum ein Histogramm betrachtet:

sns.histplot(penguins, x="flipper_length_mm", hue="species", element="poly")

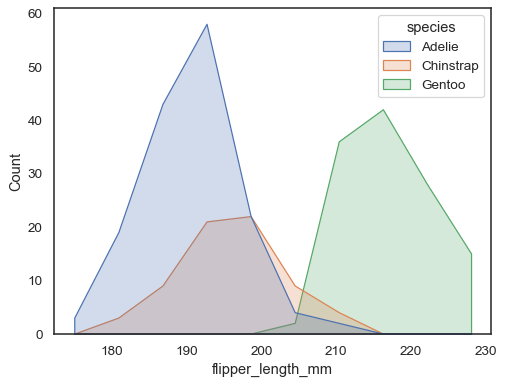
Um die Verteilung von Teilmengen zu vergleichen, die sich in der Größe erheblich unterscheiden, verwenden Sie eine unabhängige Dichtenormalisierung:

sns.histplot( penguins, x="bill_length_mm", hue="island", element="step", stat="density", common_norm=False,)

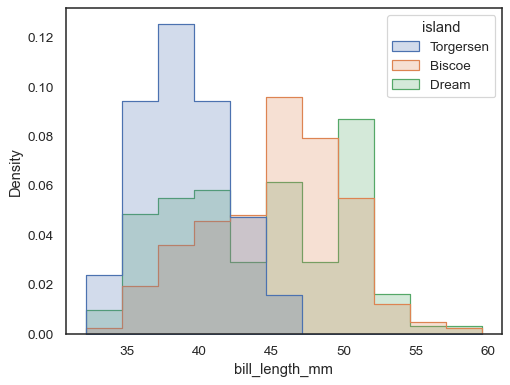
Es ist auch möglich, so zu normalisieren, dass die Höhe jedes Balkens eine Wahrscheinlichkeit aufweist, die für diskrete Variablen sinnvoller ist:

tips = sns.load_dataset("tips")sns.histplot(data=tips, x="size", stat="probability", discrete=True)

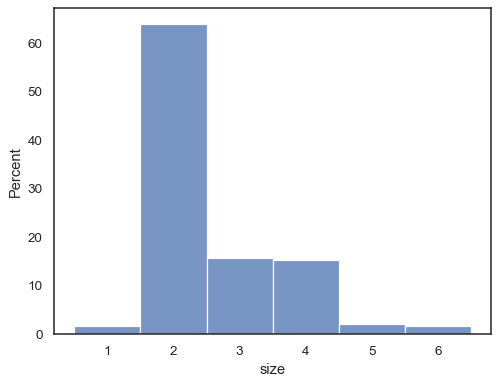
Sie können sogar ein Histogramm über kategoriale Variablen zeichnen (obwohl dies eine experimentelle Funktion ist):

sns.histplot(data=tips, x="day", shrink=.8)

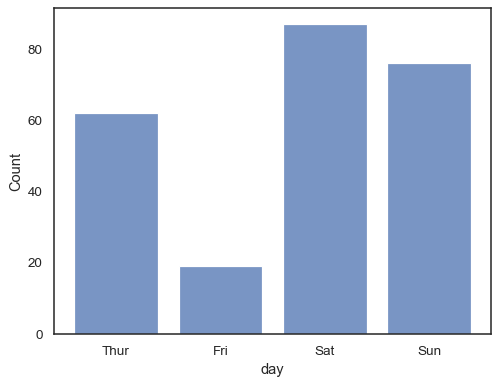
Bei Verwendung einer hue Semantik mit diskreten Daten kann es sinnvoll sein, den Ebenen auszuweichen:

sns.histplot(data=tips, x="day", hue="sex", multiple="dodge", shrink=.8)

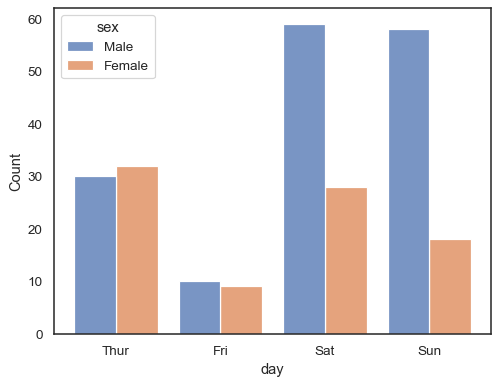
Reale Daten sind oft verzerrt. Bei stark verzerrten Verteilungen ist es besser, die Bins im Protokollbereich zu definieren. Vergleichen:

planets = sns.load_dataset("planets")sns.histplot(data=planets, x="distance")

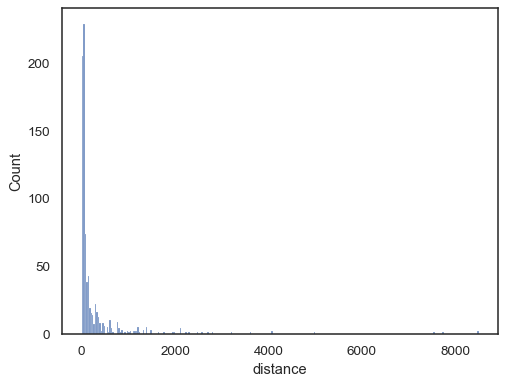
To the log-scale version:

sns.histplot(data=planets, x="distance", log_scale=True)

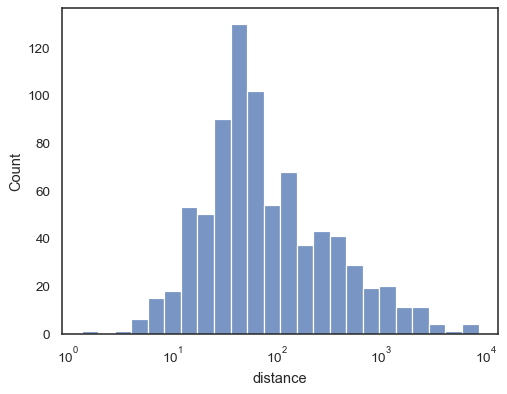
There are also a number of options for how the histogram appears. Youcan show unfilled bars:

sns.histplot(data=planets, x="distance", log_scale=True, fill=False)

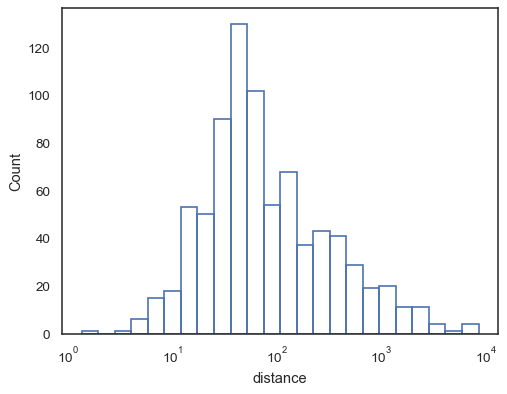
Or an unfilled step function:

sns.histplot(data=planets, x="distance", log_scale=True, element="step", fill=False)

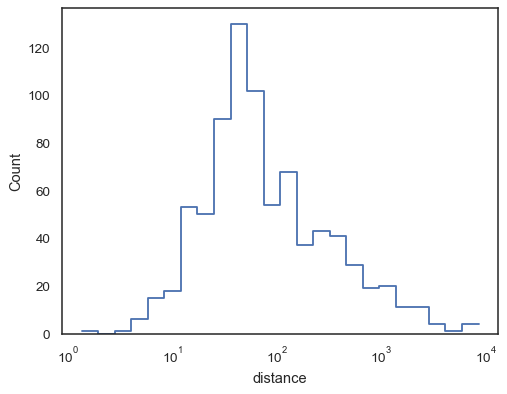
Schritt funktionen, esepcially wenn ungefüllt, machen es einfach zu comparecumulative histogramme:

sns.histplot( data=planets, x="distance", hue="method", hue_order=, log_scale=True, element="step", fill=False, cumulative=True, stat="density", common_norm=False,)

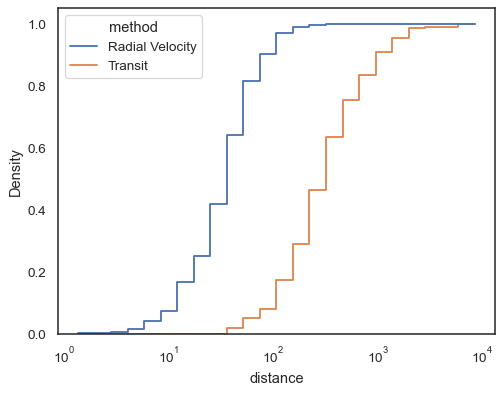
Wenn beide x und y zugewiesen sind, wird ein bivariates Histogramm berechnet und als Heatmap angezeigt:

sns.histplot(penguins, x="bill_depth_mm", y="body_mass_g")

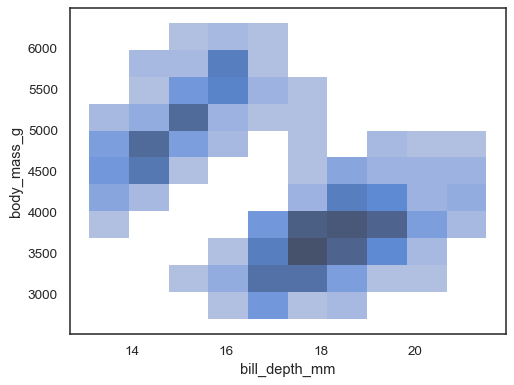
Es ist auch möglich, eine hue Variable zuzuweisen, obwohl dies nicht gut funktioniert, wenn Daten aus den verschiedenen Ebenen erhebliche Überlappungen aufweisen:

sns.histplot(penguins, x="bill_depth_mm", y="body_mass_g", hue="species")

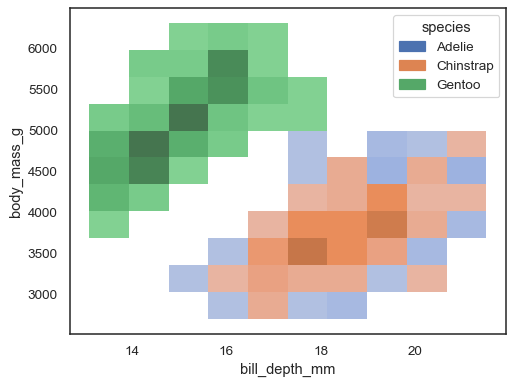
Mehrere Farbkarten können sinnvoll sein, wenn eine der Variablen istdiskret:

sns.histplot( penguins, x="bill_depth_mm", y="species", hue="species", legend=False)

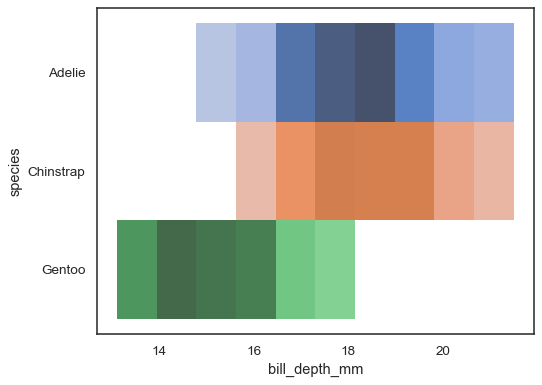
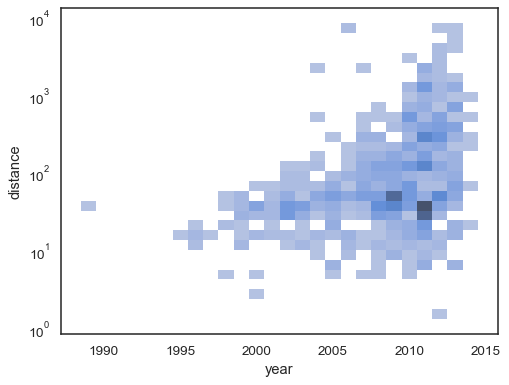
Das bivariate Histogramm akzeptiert alle gleichen Berechnungsoptionen wie sein univariates Gegenstück und verwendet Tupel, um x undy unabhängig voneinander zu parametrisieren:

sns.histplot( planets, x="year", y="distance", bins=30, discrete=(True, False), log_scale=(False, True),)

../_images/histplot_45_0.png

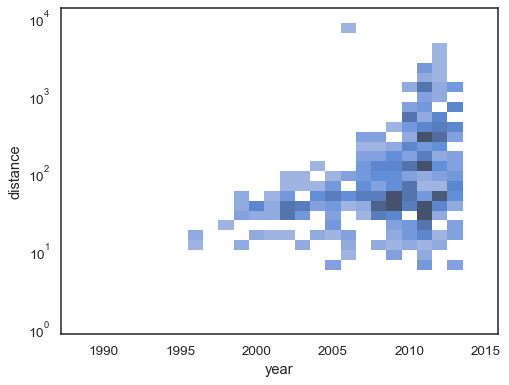
Das Standardverhalten macht Zellen ohne Beobachtungen transparent, obwohl dies deaktiviert werden kann:

sns.histplot( planets, x="year", y="distance", bins=30, discrete=(True, False), log_scale=(False, True), thresh=None,)

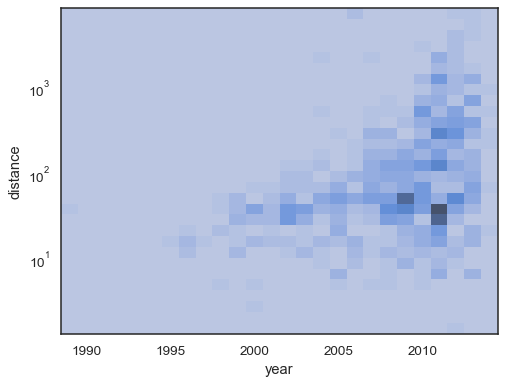
Es ist auch möglich, den Schwellenwert und den Sättigungspunkt der Farbkarte für den Anteil der kumulierten Zählungen festzulegen:

sns.histplot( planets, x="year", y="distance", bins=30, discrete=(True, False), log_scale=(False, True), pthresh=.05, pmax=.9,)

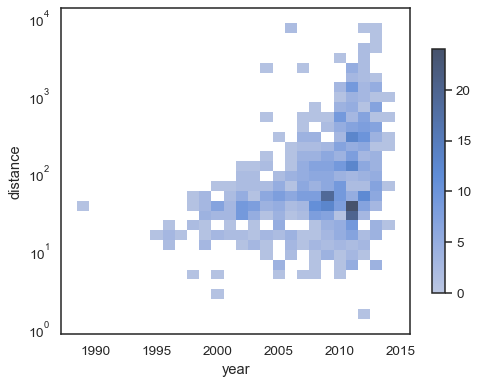
Um die Farbkarte zu kommentieren, fügen Sie eine Farbleiste hinzu:

sns.histplot( planets, x="year", y="distance", bins=30, discrete=(True, False), log_scale=(False, True), cbar=True, cbar_kws=dict(shrink=.75),)