Eine gaußsche Funktion ist eine stetige Funktion, bei der die Fläche 1 ist. Dies ermöglicht es uns, Wahrscheinlichkeiten darzustellen. Wir sind auf einer Wahrscheinlichkeit zur Normalverteilung. Die Unimodalität der Kalman-Filter bedeutet, dass wir jedes Mal einen einzelnen Peak haben, um den Zustand des Systems abzuschätzen.

Wir haben einen Mittelwert μ, der einen Zustand darstellt, und eine Varianz σ2, die eine Unsicherheit darstellt. Je größer die Varianz, desto größer die Unsicherheit.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Wir verwenden die Beobachtungen unserer Sensoren, um den vorhergesagten Zustand zu korrigieren und eine genauere Schätzung zu erhalten.

Um eine Schätzung vorzunehmen, benötigt ein Kalman-Filter nur aktuelle Beobachtungen und die vorherige Vorhersage. Die Messhistorie ist nicht notwendig.

Mathematik

Die Mathematik hinter den Kalman-Filtern besteht aus Additionen und Multiplikationen von Matrizen. Wir haben zwei Phasen: Vorhersage und Aktualisierung.

Vorhersage
Unsere Vorhersage besteht darin, einen Zustand x‘ und eine Unsicherheit P‘ zum Zeitpunkt t aus den vorherigen Zuständen x und P zum Zeitpunkt t-1 zu schätzen.

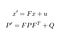
• F: Übergangsmatrix von t-1 nach t
• ν: Rauschen hinzugefügt
• Q: Kovarianzmatrix einschließlich Rauschen

Update
Die Update-Phase besteht darin, eine z-Messung von einem Sensor zu verwenden, um unsere Vorhersage zu korrigieren und somit x und P vorherzusagen.

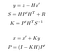
• y: Unterschied zwischen tatsächlicher Messung und Vorhersage, dh dem Fehler.
• S: Geschätzter Systemfehler
• H: Matrix des Übergangs zwischen der Markierung des Sensors und unserer.
• R: Kovarianzmatrix bezogen auf das Sensorrauschen (vom Sensorhersteller angegeben).
• K: Kalman-Gewinn. Koeffizient zwischen 0 und 1, der die Notwendigkeit widerspiegelt, unsere Vorhersage zu korrigieren.

Die Aktualisierungsphase ermöglicht es, ein x und ein P näher an der Realität abzuschätzen, als die Messungen liefern.

Ein Kalman-Filter ermöglicht Vorhersagen in Echtzeit, ohne vorhergehende Daten. Wir verwenden ein mathematisches Modell, das auf der Multiplikation von Matrizen basiert und für jedes Mal einen Zustand x (Position, Geschwindigkeit) und eine Unsicherheit P definiert.

Représentation Prior/Posterior

Dieses Diagramm zeigt, was in einem Kalman-Filter passiert.

• Die vorhergesagte Zustandsschätzung stellt unsere erste Schätzung dar, unsere Vorhersagephase. Wir sprechen über Prior.
• Messung ist die Messung von einem unserer Sensoren. Wir haben eine bessere Unsicherheit, aber das Rauschen der Sensoren macht es zu einer Messung, die immer schwer abzuschätzen ist. Wir sprechen von Wahrscheinlichkeit.
• Die optimale Zustandsschätzung ist unsere Aktualisierungsphase. Die Unsicherheit ist diesmal die schwächste, wir haben Informationen gesammelt und einen Wert generieren lassen, der sicherer ist als mit unserem Sensor allein. Dieser Wert ist unsere beste Vermutung. Wir sprechen von posterior.

Was ein Kalman-Filter implementiert, ist eigentlich eine Bayes-Regel.

In einem Kalman-Filter schleifen wir Vorhersagen aus Messungen. Unsere Vorhersagen sind immer präziser, da wir ein gewisses Maß an Unsicherheit beibehalten und regelmäßig den Fehler zwischen unserer Vorhersage und der Realität berechnen. Wir sind in der Lage, aus Matrixmultiplikationen und Wahrscheinlichkeitsformeln Geschwindigkeiten und Positionen von Fahrzeugen um uns herum zu schätzen.

„Erweiterte/Unscented“ Filter und Nichtlinearität

Ein wesentliches Problem entsteht. Unsere mathematischen Formeln sind alle mit linearen Funktionen vom Typ y = ax + b implementiert.
Ein Kalman-Filter arbeitet immer mit linearen Funktionen. Wenn wir jedoch ein Radar verwenden, sind die Daten nicht linear.

Das Radar sieht die Welt mit drei Maßen:

Diese drei Werte machen unsere Messung unter Einbeziehung des Winkels φ zu einer nichtlinearen.

Unser Ziel ist es, die Daten ρ, φ, ρ in kartesische Daten (px, py, vx, vy) umzuwandeln.

Wenn wir nichtlineare Daten in einen Kalman-Filter eingeben, liegt unser Ergebnis nicht mehr in unimodaler Gaußscher Form vor und wir können Position und Geschwindigkeit nicht mehr schätzen.

Wir verwenden also Näherungen, weshalb wir an zwei Methoden arbeiten:
– Erweiterte Kalman-Filter verwenden Jacobian- und Taylor-Reihen, um das Modell zu linearisieren.
– Unscented Kalman-Filter verwenden eine genauere Annäherung an das Modell linearisieren.

Um mit der Einbeziehung der Nichtlinearität durch das Radar umzugehen, existieren Techniken, die es unseren Filtern ermöglichen, die Position und Geschwindigkeit der Objekte zu schätzen, die wir verfolgen möchten.