Ein integraler Bestandteil der Fluiddynamik ist die Vorticity. Heuristisch misst es die lokale Rotation eines Fluidpakets. Für feste Objekte sprechen wir nicht von der Wirbeligkeit eines Objekts, sondern von seiner Winkelgeschwindigkeit. Diese beiden Konzepte sind verwandt, aber die Vortizität ist nützlicher, wenn rotierende Objekte diskutiert werden, die sich verformen, wie es eine Flüssigkeit tut.

Die Vortizität eines gegebenen Geschwindigkeitsfeldes innerhalb einer gegebenen Ebene wird berechnet, indem zwei beliebige orthogonale Achsen in dieser Ebene ausgewählt und die Winkelgeschwindigkeit jeder Achse addiert werden. In einem festen Objekt oder einer Flüssigkeit, die sich wie ein festes Objekt dreht (treffend als Festkörperrotation bezeichnet), ist die Vortizität doppelt so groß wie die Winkelgeschwindigkeit, da sich jede Achse mit der gleichen Geschwindigkeit dreht. In einer Flüssigkeit können sich die beiden Achsen jedoch mit sehr unterschiedlichen Geschwindigkeiten und sogar in verschiedene Richtungen drehen! Es ist sogar möglich, dass sich jede Achse drehen kann, aber die Nettowirtizität Null ist (siehe Irrotationswirbel).

Wenn die Bewegung eines Fluids streng darauf beschränkt ist, in einer Ebene zu liegen, dann wird angenommen, dass der Wirbelvektor orthogonal zur Ebene ist und die Richtung (oder Neigung) nicht ändern kann. Der einzige Aspekt des Wirbels, der sich ändern kann, ist seine Größe. Es wird angenommen, dass diese Übertragung von Energie auf größere Skalen mit der Bildung des Großen Roten Flecks auf Jupiter zusammenhängt.

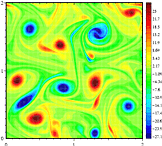
In der dreidimensionalen Fluidbewegung ist der Wirbelvektor dreidimensional, da er Komponenten parallel zu jeder Achse, x, y und z aufweist: Die z-Komponente ist parallel zur z-Achse und beschreibt die Rotationsrate in der xy-Ebene. Aufgrund dieser Dichotomie gibt es einen qualitativen Unterschied im Verhalten zwischen zweidimensionalen Turbulenzen und dreidimensionalen Turbulenzen. In ersterem besteht die Tendenz, dass Wirbel zusammenklumpen und größere Wirbel bilden, während in letzterem die Wirbelbewegungen auseinandergerissen werden und die Energie bis auf die kleinsten Skalen kaskadiert, wo sie dann wegdiffundiert wird.

Mathematisch ist die Wirbeligkeit eines gegebenen Geschwindigkeitsfeldes,

definiert als die Krümmung des Geschwindigkeitsfeldes und wird normalerweise mit dem griechischen Buchstaben omega bezeichnet,

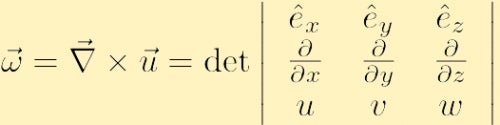
wo wir das herkömmliche Nabla-Symbol für den Farbverlauf verwendet haben:

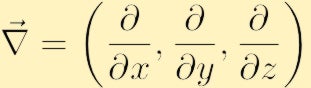
In Komponentenform wird die Vortizität durch Erweitern der obigen Determinante gefunden,

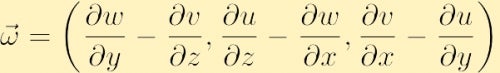
Ein weiterer wichtiger Aspekt der Fluiddynamik, der mit der Vortizität zusammenhängt, ist die Zirkulation. Im Gegensatz zur Vortizität, die eine lokale Eigenschaft ist, die an jedem Punkt im Raum definiert ist, ist die Zirkulation eine globale Eigenschaft, die durch die Integration einer Eigenschaft der Flüssigkeit über eine Kurve definiert wird. Insbesondere wenn Sie eine geschlossene Kontur auswählen und sie mit dem Buchstaben C(t) bezeichnen, ist die Zirkulation um C(t) gegen den Uhrzeigersinn eine skalare Größe, die mit

definiert ist als,

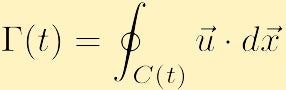
eine Funktion der Zeit, ebenso wie die geschlossene Kontur.

Nehmen wir uns einen Moment Zeit, um zu erklären, was das physisch bedeutet. An jedem Punkt der Kontur C (t) finden wir die Komponente der Geschwindigkeit, die tangential zur Kurve ist, und multiplizieren diesen Skalar mit einer infinitesimalen Länge; die Projektion der Geschwindigkeit auf die Tangente ergibt notwendigerweise eine Größe zwischen der Geschwindigkeit an dieser Position und Null. Wenn die Geschwindigkeit tangential zur Kurve ist, erhalten wir plus oder minus der Geschwindigkeit von , wenn die Geschwindigkeit orthogonal zur Kurve ist, erhalten wir Null. Dann integrieren wir diese Menge, eine andere Art zu sagen, eine unendliche Anzahl von Dingen zu summieren, um die Kontur herum, so dass wir den Beitrag von jedem Punkt aus hinzufügen. Daraus ermitteln wir, dass die Zirkulation entlang einer Kontur C (t) die Strömungsmenge um die Kontur C (t) ist; ein positives oder negatives Ergebnis entspricht einer Zirkulation im Uhrzeigersinn bzw. im Uhrzeigersinn. Ein extremer Fall ist, dass das Geschwindigkeitsfeld überall senkrecht zur Kurve C (t) steht und folglich keine Zirkulation stattfindet, da die Strömung immer die Kontur überquert und niemals entlang der Kontur fließt. Um eine Zirkulation ungleich Null zu erhalten, muss ein Teil der Kurve vorhanden sein, in dem sich die Strömung entlang der geschlossenen Kontur befindet.

Wenn das Geschwindigkeitsfeld glatt ist und es keine Singularitäten innerhalb von C(t) gibt, können wir den Integralsatz von Stokes aus der Vektorrechnung verwenden, um die Zirkulation neu zu schreiben als,

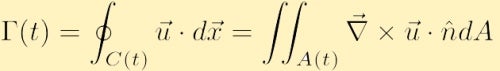
wobei A die Fläche ist, die innerhalb der Kontur C enthalten ist, und t der Einheitsnormalvektor zur Fläche I ist.

Bevor wir diese neue Gleichung für die Zirkulation betrachten, ist es nützlich, die physikalische Bedeutung für den Satz von Stokes zu verstehen, wo das Vektorfeld die Geschwindigkeit ist. Im obigen Doppelintegral berechnen wir die Vortizität an jedem Punkt innerhalb der Kontur und summieren dann die Vortizität über alle diese Punkte in A(t). Im einzelnen Integral über die geschlossene Kontur berechnen wir den Fluss entlang der Grenze des Bereichs. Der Satz von Stokes besagt dann, dass diese Größen gleich sind, und somit, dass, wenn es eine mittlere Vortizität innerhalb eines Bereichs gibt, was dann bedeuten muss, dass der Bereich eine Rotationsrate ungleich Null hat, folglich eine Nettozirkulation entlang des Umfangs dieser Grenze vorhanden sein muss.

Aus dem Mittelwertsatz der Infinitesimalrechnung können wir den Integranden im Doppelintegral durch einen Mittelwert ersetzen, der der Mittelkomponente der Wirbel orthogonal zu der Ebene entspricht, in der C(t) liegt. Daher ist die zweite Interpretation der Zirkulation, dass es die mittlere Vortizität mal die Fläche innerhalb von C (t) ist. Anstatt die Zirkulation auf der geschlossenen Kontur C (t) zu berechnen, können wir die mittlere Vortizität normal zu A (t) berechnen und diese mit der Fläche innerhalb multiplizieren. Wenn Sie den Sonderfall betrachten, in dem die Vortizität überall konstant ist, wäre die Zirkulation die Größe der Vortizität mal der darin enthaltenen Fläche.

Ein Punktwirbel ist ein Wirbel, der keine Fläche hat, was bedeutet, dass Wirbel nur an einem einzigen Punkt vorhanden sind. Um Punktwirbel zu untersuchen, nehmen wir zunächst an, dass wir eine inkompressible 2D-Strömung haben. (Punktwirbel werden manchmal auch als Linienwirbel bezeichnet, wenn sie in 3D betrachtet werden.)

Nach einigen Berechnungen stellen wir fest, dass das Geschwindigkeitsfeld, das von einem Punktwirbel in komplexer Form erzeugt wird, der sich bei z0 befindet, gegeben ist durch (wobei Gamma Zero die Zirkulation um den Punktwirbel ist, die oft als die Stärke des Punktwirbels bezeichnet wird):

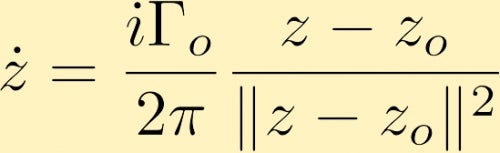
Das von einem Punktwirbel erzeugte Geschwindigkeitsfeld kann dazu führen, dass sich ein anderer Punktwirbel bewegt. Hier sind einige Beispiele dafür: Die zwei Punktwirbel, beide positiv und von gleicher Größe, die zwei Punktwirbel, beide positiv, aber einer hat die dreifache Stärke des anderen und ein Punktwirbel ist negativ mit der doppelten Größe des anderen, der positiv ist . Eine andere Möglichkeit besteht darin, zwei Punktwirbel gleicher Größe, aber entgegengesetztem Vorzeichen zu betrachten.

Dies kann auf eine beliebige Anzahl von Punktwirbeln erweitert werden, N. Die Bewegungsgleichung in komplexer Form für einen Punktwirbel alpha ist gegeben durch:

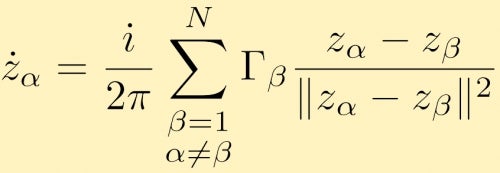
Das Betrachten der Wechselwirkungen von Punktwirbeln ist ein sehr interessantes Problem, das analytisch schwierig zu lösen ist, insbesondere wenn die Anzahl der Punktwirbel zunimmt. Numerische Simulationen von Punktwirbel-Wechselwirkungen sind daher sehr verbreitet. Eine nützliche Anwendung von Großpunktwirbelsimulationen ist, wenn Sie große Cluster von Punktwirbeln betrachten, die Wirbel mit endlicher Fläche simulieren. Hier finden Sie Beschreibungen und die Ergebnisse mehrerer Großpunkt-Wirbelsimulationen. In diesem Fall verschmelzen zwei große Cluster von Punktwirbeln gleicher Stärke. Im nächsten Fall beginnen wir mit einem Ring von geclusterten Punktwahrheiten.

Um eine Gleichung für die Entwicklung der Wirbel zu finden, beginnen wir mit der Impulsgleichung. In der Impulsgleichung kann der advektive Term wie folgt umgeschrieben werden:

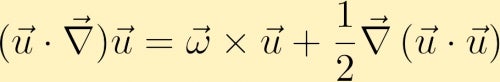
Als nächstes berechnen wir die Wellung der Impulsgleichung und durch einige Vektoridentitäten erhalten wir die Wirbelgleichung:

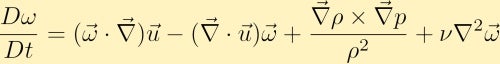
Die Wirbelgleichung zeigt, wie Wirbel in einer Flüssigkeit erzeugt werden können. Ohne Verlust der Allgemeinheit gehen wir davon aus, dass wir anfangs nur Wirbel in z-Richtung haben. Daraus können wir sehen, wie jeder der vier verschiedenen Terme die Vortizität verändern kann.

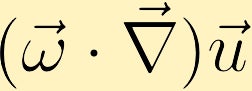
Wenn sich die Geschwindigkeit mit der Richtung der vorhandenen Wirbel ändert, kann Wirbel erzeugt werden.

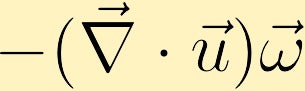
Wenn sich ein Fluidpaket ausdehnt und die Vortizität positiv ist, nimmt die Vortizität des Fluidpakets ab und wenn sich das Paket zusammenzieht, nimmt die Vortizität zu.

Flüssigkeitsschichten konstanter Dichte (Isopycnale) wollen mit Schichten konstanten Drucks (Isobaren) zusammenfallen. Wenn diese Schichten nicht übereinstimmen, beginnt sich die Flüssigkeit zu drehen, damit sie sich ausrichten, wodurch Wirbel erzeugt werden. (Im Beispiel beginnen wir mit Null Wirbel.)

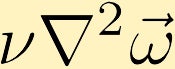
Viskose Kräfte verursachen die Diffusion von Wirbelkörpern. (Im Beispiel beginnen wir mit einem Punkt unendlicher Vortizität in der Mitte.)