Blog
En una publicación de blog anterior, analizamos cómo los supermercados utilizan los datos para comprender mejor las necesidades de los consumidores y, en última instancia, aumentar su gasto general. Una de las técnicas clave utilizadas por los grandes minoristas es el Análisis de la Cesta de Mercado (MBA), que descubre asociaciones entre productos al buscar combinaciones de productos que con frecuencia se producen en las transacciones. En otras palabras, permite a los supermercados identificar las relaciones entre los productos que la gente compra. Por ejemplo, es probable que los clientes que compran un lápiz y papel compren una goma o una regla.
» El análisis de la cesta de mercado permite a los minoristas identificar las relaciones entre los productos que compran las personas.»
Los minoristas pueden utilizar los conocimientos adquiridos de MBA de varias maneras, entre ellas:
- Agrupar productos que se producen conjuntamente en el diseño del diseño de una tienda para aumentar las posibilidades de ventas cruzadas;
- Impulsar motores de recomendación en línea («los clientes que compraron este producto también vieron este producto»); y
- Segmentar campañas de marketing mediante el envío de cupones promocionales a los clientes para productos relacionados con artículos que compraron recientemente.
Dado lo popular y valioso que es MBA, pensamos en producir la siguiente guía paso a paso que describe cómo funciona y cómo podría llevar a cabo su propio Análisis de Cesta de Mercado.
¿Cómo funciona el Análisis de la Cesta de Mercado?
Para realizar un MBA, primero necesitará un conjunto de datos de transacciones. Cada transacción representa un grupo de artículos o productos que se han comprado juntos y que a menudo se conocen como un «conjunto de artículos». Por ejemplo, un conjunto de artículos podría ser: {lápiz, papel, grapas, goma} en cuyo caso todos estos artículos se han comprado en una sola transacción.
En un MBA, las transacciones se analizan para identificar las reglas de asociación. Por ejemplo, una regla podría ser: {lápiz, papel} => {goma}. Esto significa que si un cliente tiene una transacción que contiene un lápiz y papel, es probable que también esté interesado en comprar una goma.
Antes de aplicar una regla, un minorista necesita saber si hay pruebas suficientes que sugieran que dará lugar a un resultado beneficioso. Por lo tanto, medimos la fuerza de una regla calculando las tres métricas siguientes (tenga en cuenta que hay otras métricas disponibles, pero estas son las tres más utilizadas):
Soporte: el porcentaje de transacciones que contienen todos los elementos de un conjunto de elementos (por ejemplo, lápiz, papel y goma). Cuanto mayor sea el soporte, más frecuentemente se produce el conjunto de artículos. Se prefieren las reglas con un alto soporte, ya que es probable que sean aplicables a un gran número de transacciones futuras.
Confianza: la probabilidad de que una transacción que contiene los elementos en el lado izquierdo de la regla (en nuestro ejemplo, lápiz y papel) también contenga el elemento en el lado derecho (una goma). Cuanto mayor sea la confianza, mayor será la probabilidad de que se compre el artículo en el lado derecho o, en otras palabras, mayor será la tasa de retorno que puede esperar para una regla dada.
Levante: la probabilidad de que todos los elementos de una regla ocurran juntos (también conocido como el soporte) dividido por el producto de las probabilidades de que los elementos del lado izquierdo y derecho ocurran como si no hubiera asociación entre ellos. Por ejemplo, si el lápiz, el papel y el caucho aparecen juntos en el 2,5% de todas las transacciones, el lápiz y el papel en el 10% de las transacciones y el caucho en el 8% de las transacciones, entonces el elevador sería: 0.025/(0.1*0.08) = 3.125. Una elevación de más de 1 sugiere que la presencia de lápiz y papel aumenta la probabilidad de que también se produzca una goma en la transacción. En general, la elevación resume la fuerza de asociación entre los productos en el lado izquierdo y derecho de la regla; cuanto mayor sea la elevación, mayor será el vínculo entre los dos productos.
Para realizar un Análisis de Cesta de Mercado e identificar reglas potenciales, se usa comúnmente un algoritmo de minería de datos llamado «algoritmo Apriori», que funciona en dos pasos:
- Identificar sistemáticamente conjuntos de elementos que ocurren con frecuencia en el conjunto de datos con un soporte mayor que un umbral preestablecido.
- Calcule la confianza de todas las reglas posibles dados los conjuntos de artículos frecuentes y mantenga solo aquellos con una confianza mayor que un umbral predeterminado.
Los umbrales para establecer el soporte y la confianza son especificados por el usuario y es probable que varíen entre los conjuntos de datos de transacción. R tiene valores predeterminados, pero le recomendamos que experimente con ellos para ver cómo afectan al número de reglas devueltas (más sobre esto a continuación). Finalmente, aunque el algoritmo Apriori no usa lift para establecer reglas, verás en lo siguiente que usamos lift al explorar las reglas que devuelve el algoritmo.
Realizar Análisis de Cesta de mercado en R
Para demostrar cómo realizar un MBA, hemos elegido utilizar R y, en particular, el paquete arules. Para aquellos que estén interesados, hemos incluido el código R que usamos al final de este blog.
Aquí, seguimos el mismo ejemplo utilizado en la viñeta de arulesViz y usamos un conjunto de datos de ventas de comestibles que contiene 9,835 transacciones individuales con 169 artículos. Lo primero que hacemos es echar un vistazo a los elementos de las transacciones y, en particular, trazar la frecuencia relativa de los 25 elementos más frecuentes de la Figura 1. Esto es equivalente al soporte de estos elementos donde cada conjunto de elementos contiene solo un elemento. Esta gráfica de barra ilustra los comestibles que se compran con frecuencia en esta tienda, y es notable que el soporte incluso de los artículos más frecuentes es relativamente bajo (por ejemplo, el artículo más frecuente se produce en solo alrededor del 2,5% de las transacciones). Utilizamos estos conocimientos para informar el umbral mínimo al ejecutar el algoritmo Apriori; por ejemplo, sabemos que para que el algoritmo devuelva un número razonable de reglas, necesitaremos establecer el umbral de soporte muy por debajo de 0.025.
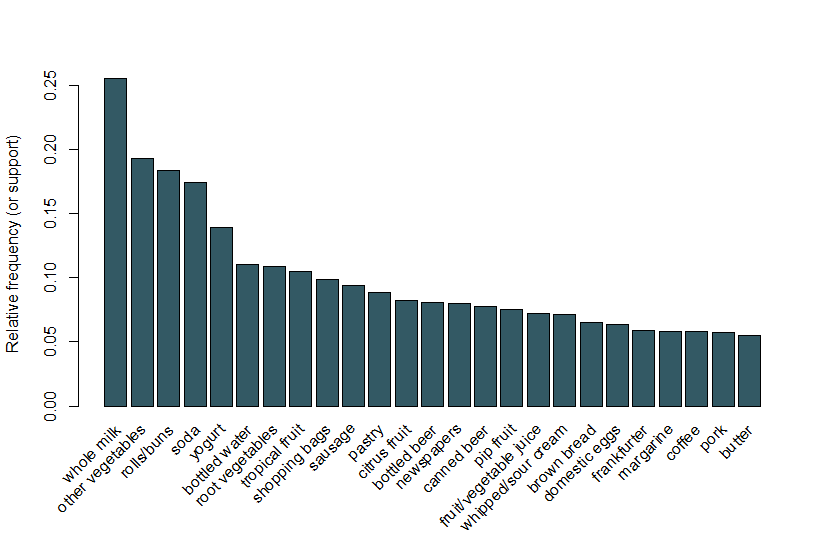
Figura 1 Gráfico de barras de soporte de los 25 artículos más frecuentes comprados.
Al establecer un umbral de soporte de 0,001 y una confianza de 0,5, podemos ejecutar el algoritmo Apriori y obtener un conjunto de 5.668 resultados. Estos valores de umbral se eligen para que el número de reglas devueltas sea alto, pero este número se reduciría si aumentáramos cualquiera de los umbrales. Recomendamos experimentar con estos umbrales para obtener los valores más adecuados. Si bien hay demasiadas reglas para poder verlas todas de forma individual, podemos ver las cinco reglas con la mayor elevación:
| Regla | Soporte | Confianza | Lift |
| {productos alimenticios instantáneos,soda}=>{carne de hamburguesa} | 0.001 | 0.632 | 19.00 |
| {soda, palomitas de maíz}=>{snacks salados} | 0,001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. Por ejemplo, la primera regla podría representar el tipo de artículos comprados para una barbacoa, la segunda para una noche de cine y la tercera para hornear.
En lugar de usar los umbrales para reducir las reglas a un conjunto más pequeño, es habitual que se devuelva un conjunto más grande de reglas para que haya una mayor probabilidad de generar reglas relevantes. Alternativamente, podemos usar técnicas de visualización para inspeccionar el conjunto de reglas devueltas e identificar aquellas que probablemente sean útiles.
Usando el paquete arulesViz, trazamos las reglas por confianza, soporte y elevación en la Figura 2. Este gráfico ilustra la relación entre las diferentes métricas. Se ha demostrado que las reglas óptimas son las que se encuentran en lo que se conoce como el»límite de confianza en el soporte». Esencialmente, estas son las reglas que se encuentran en el borde derecho de la trama donde se maximiza el apoyo, la confianza o ambos. La función de trazado en el paquete arulesViz tiene una útil función interactiva que le permite seleccionar reglas individuales (haciendo clic en el punto de datos asociado), lo que significa que las reglas en el borde se pueden identificar fácilmente.
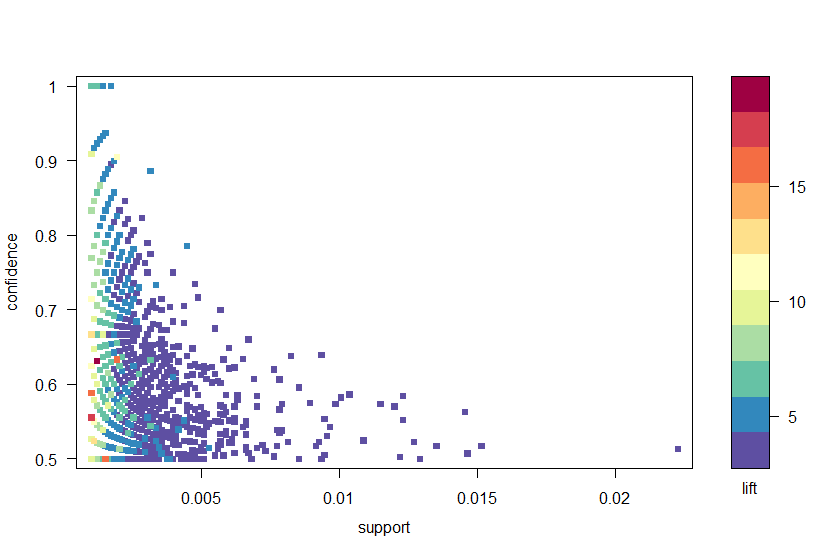
Figura 2: Gráfico de dispersión de las métricas de confianza, soporte y elevación.
Hay muchas otras gráficas disponibles para visualizar las reglas, pero otra figura que recomendamos explorar es la visualización basada en gráficos (consulte la Figura 3) de las diez reglas principales en términos de elevación (puede incluir más de diez, pero este tipo de gráficas puede desordenarse fácilmente). En este gráfico, los elementos agrupados alrededor de un círculo representan un conjunto de elementos y las flechas indican la relación en las reglas. Por ejemplo, una regla es que la compra de azúcar está asociada con la compra de harina y levadura en polvo. El tamaño del círculo representa el nivel de confianza asociado con la regla y el color, el nivel de elevación (cuanto mayor sea el círculo y más oscuro el gris, mejor).
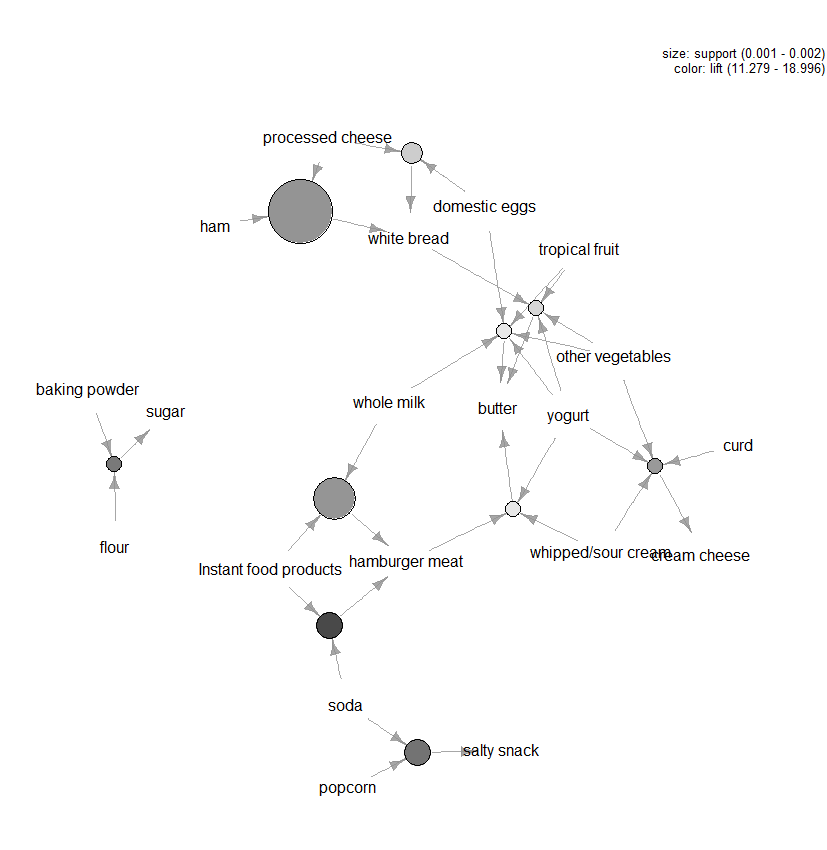
Figura 3: Visualización basada en gráficos de las diez reglas principales en términos de elevación.
El análisis de la cesta de mercado es una herramienta útil para los minoristas que desean comprender mejor las relaciones entre los productos que la gente compra. Hay muchas herramientas que se pueden aplicar al realizar MBA y los aspectos más complicados del análisis son establecer los umbrales de confianza y soporte en el algoritmo Apriori e identificar qué reglas vale la pena seguir. Por lo general, esto último se hace midiendo las reglas en términos de métricas que resumen lo interesantes que son, utilizando técnicas de visualización y también estadísticas multivariadas más formales. En última instancia, la clave de MBA es extraer valor de los datos de sus transacciones mediante la construcción de una comprensión de las necesidades de sus consumidores. Este tipo de información es invaluable si está interesado en actividades de marketing, como ventas cruzadas o campañas específicas.
Si desea obtener más información sobre cómo analizar los datos de sus transacciones, póngase en contacto con nosotros y estaremos encantados de ayudarle.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.