La refracción, o flexión de la luz, ocurre cuando la luz pasa de un medio a otro con un índice de refracción diferente. La refracción es una característica importante de las lentes, que les permite enfocar un haz de luz en un solo punto, y también es responsable de una variedad de fenómenos familiares, como la distorsión aparente de objetos parcialmente sumergidos en agua.

El índice de refracción se define como la velocidad relativa a la que la luz se mueve a través de un material con respecto a su velocidad en el vacío. Por convención, el índice de refracción de un vacío se define como un valor de 1,0. El índice de refracción, n, de otros materiales transparentes se define mediante la ecuación:

donde c es la velocidad de la luz, y v es la velocidad de la luz en el material. Dado que el índice de refracción de un vacío se define como 1.0 y un vacío está desprovisto de cualquier material, los índices de refracción de todos los materiales transparentes son por lo tanto mayores que 1.0. Para la mayoría de los propósitos prácticos, el índice de refracción de la luz a través del aire (1.0003) se puede usar para calcular índices de refracción de materiales desconocidos. En el cuadro 1 se presentan los índices de refracción de algunos materiales comunes.

Material Índice de Refracción Aire 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Por ejemplo, cuando la luz pasa de un medio menos denso, como el aire, a un medio más denso, como el agua, la velocidad a la que viaja la onda electromagnética disminuye. Alternativamente, cuando la luz pasa de un medio más denso a un medio menos denso, la velocidad de la onda aumenta.

El ángulo en el que viaja la luz refractada, sin embargo, depende tanto del ángulo de incidencia como de la composición del material en el que está entrando. Lo normal se puede definir como una línea perpendicular al límite entre dos sustancias. La luz pasa al límite en un ángulo con respecto a la normal y se refracta de acuerdo con la Ley de Snell:

donde n representa los índices de refracción del material 1 y el material 2 y q simboliza los ángulos de luz que viajan a través de estos materiales con respecto a la normal. Hay varios puntos importantes que se pueden extraer de esta ecuación. Cuando n(1) es mayor que n(2), el ángulo de refracción es siempre menor que el ángulo de incidencia. Alternativamente, cuando n(2) es mayor que n (1), el ángulo de refracción es siempre mayor que el ángulo de incidencia. Cuando los dos índices de refracción son iguales (n(1) = n (2)), entonces la luz pasa sin refracción.

El concepto de índice de refracción se ilustra en la Figura 1 a continuación, centrándose en el caso de la luz que pasa del aire a través del vidrio y el agua. Observe que mientras ambos haces entran en el material más denso a través del mismo ángulo de incidencia con respecto al normal (60 grados), la refracción para el vidrio es casi 6 grados mayor que la del agua debido al mayor índice de refracción del vidrio.

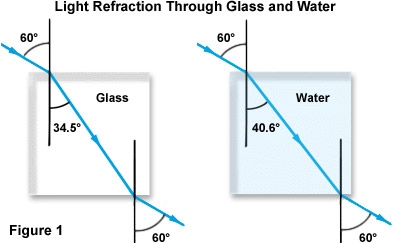
los Científicos han encontrado que el índice de refracción varía con la frecuencia de la radiación (o longitud de onda) de la luz. Este fenómeno ocurre en conjunto con todos los medios transparentes y se ha denominado dispersión. Por lo tanto, al medir el índice de refracción de una sustancia transparente, se debe identificar la longitud de onda particular utilizada en la medición. A continuación, la Tabla 2 detalla la dispersión de tres longitudes de onda independientes en varios medios.

Material Azul (486.1 nm) Amarillo (589.3 nm) Rojo (656.3 nm) Corona de Cristal 1.524 1.517 1.515 Flint Glass 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Esta luz se denomina espectro de la línea D, y representa la luz amarilla listada en la Tabla 2 anterior. Del mismo modo, los espectros de la línea F y de la línea C corresponden a la luz azul y roja de longitudes de onda específicas emitidas por el hidrógeno. Estos espectros son fundamentales en el cálculo de la dispersión, que se puede definir cuantitativamente como:

donde n es el índice de refracción del material en una longitud de onda determinada designada por D, F y C, que representan las líneas espectrales de sodio e hidrógeno como se mencionó anteriormente. La relación es tal que a medida que aumenta la longitud de onda de la luz, el índice de refracción disminuye. Sin embargo, muchos factores juegan un papel en la dispersión de diversos materiales, incluida su composición elemental y molecular. Varios sólidos inorgánicos, como cromatos, dicromatos, cianuros, vanadatos y complejos de halogenuros, tienen dispersiones inusualmente altas. Sin embargo, los sustituyentes orgánicos también pueden contribuir a una alta dispersión.

	Interactive Java Tutorial
Refracción de la luz Descubra cómo la longitud de onda y el ángulo de incidencia de la luz afectan a la refracción en una variedad de medios con diferentes índices de refracción.

Refraction of light is particularly important in the construction and physics of lenses. Recuerde que cuando el haz de luz salió tanto del vidrio como del agua en la Figura 1, se refractó de nuevo en el mismo ángulo en el que entró en el material. Este concepto es esencial en el funcionamiento de las lentes, aunque la forma de la lente afecta significativamente la imagen resultante. En una lente convexa, como se ilustra a continuación en la Figura 2, las ondas de luz reflejadas desde el objeto, en este caso una jirafa, se doblan hacia el centro óptico de la lente y convergen en el punto focal.

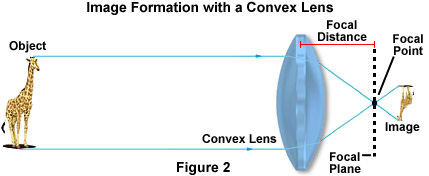
La posición relativa del objeto con respecto a la parte frontal del punto focal de la lente determina cómo el objeto es crear una imagen. Si el objeto supera el doble de la longitud del punto focal, entonces parece más pequeño e invertido y debe ser fotografiado con una lente adicional para aumentar el tamaño. Sin embargo, cuando la imagen está más cerca del objetivo que del punto focal, la imagen aparece en posición vertical y más grande, como se puede demostrar fácilmente con una simple lupa.

	Interactive Java Tutorial
Aumento de imagen Explore cómo se magnifica la imagen de una jirafa mediante la refracción de ondas de luz que pasan a través de una lente bi-convexa delgada simple.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Una simple pajita en un vaso lleno de agua, como se ilustra en la Figura 3, es un excelente ejemplo de esta ocurrencia. En este ejemplo, las ondas de luz primero deben pasar a través del agua, luego a través del límite vidrio/agua, y finalmente a través del aire. Las ondas de luz reflejadas desde los extremos de la paja se refractan en mayor grado que las que provienen del centro de la paja, lo que hace que la paja parezca ampliada y ligeramente distorsionada.

El mismo fenómeno puede ser utilizado para determinar el índice de refracción de un líquido con un microscopio óptico. Para ello, se debe colocar una celda plana capaz de contener líquido con una marca (o graduaciones) en la superficie interior del vidrio. Además, uno de los oculares del microscopio debe tener una retícula graduada insertada en el plano de imagen primario para medir el ancho de línea de la marca en la celda plana. Antes de añadir el líquido de índice de refracción desconocido a la célula, el microscopio debe centrarse en la marca en la parte inferior de la célula y anotar una medición de la posición de la marca en la retícula. A continuación, se debe agregar una pequeña cantidad de líquido a la célula y el microscopio se debe volver a enfocar en la marca (a través del líquido) y se debe realizar una nueva medición. A continuación, el microscopio debe enfocarse finalmente en la superficie del líquido y registrar una tercera lectura midiendo la posición de la marca en la retícula. El índice de refracción del líquido desconocido se puede calcular utilizando la siguiente ecuación:

donde D(medido) es la profundidad medida (desde la superficie del líquido hasta la posición de la marca en la celda vacía) utilizando el microscopio y D(aparente) es la marca medición con y sin líquido.

El ángulo crítico de reflexión es otro concepto clave en el estudio de la refracción de la luz y se ilustra a continuación en la Figura 4. Cuando la luz pasa a través de un medio de alto índice de refracción a un medio de menor índice de refracción, el ángulo incidente de las ondas de luz se convierte en un factor importante. Si el ángulo incidente aumenta más allá de un valor específico (dependiendo del índice de refracción de los dos medios), alcanzará un punto en el que el ángulo es tan grande que no se refracta luz en el medio de menor índice de refracción.

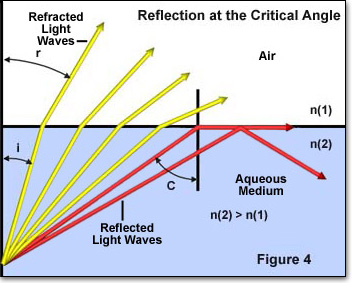
En la Figura 4, los rayos de luz individuales están representados por flechas de color rojo o amarillo que se mueven de un medio de alto índice de refracción (n(2)) a uno de menor índice de refracción (n(1)). El ángulo de incidencia de cada rayo de luz individual se denota por i y el ángulo de refracción por r. Los cuatro rayos de luz amarillos tienen un ángulo de incidencia (i) lo suficientemente bajo como para pasar a través de la interfaz entre los dos medios. Sin embargo, los dos rayos de luz roja tienen ángulos incidentes que exceden el ángulo crítico (aproximadamente 41 grados) y se reflejan en el límite entre el medio o en el medio de alto índice de refracción. Este fenómeno tiene lugar cuando el ángulo de refracción (ángulo r en la Figura 4) es igual a 90 grados y la ley de Snell se reduce a:

donde (q) ahora se denomina ángulo crítico C. Si el medio de menor índice de refracción es el aire (n = 1.00), la ecuación se reduce aún más a:

Como se mencionó anteriormente, otra característica importante de la refracción de luz es que la longitud de onda de la luz tiene un impacto en la cantidad de refracción que se produce dentro de un medio. De hecho, la cantidad de refracción que tiene lugar es inversamente proporcional a la longitud de onda de la luz incidente. Por lo tanto, la luz visible de longitud de onda más corta se refracta en un ángulo mayor que la luz de longitud de onda más larga. En consecuencia, cuando la luz blanca, que está compuesta de todos los colores del espectro visible, pasa a través de un prisma de vidrio, se dispersa en sus colores componentes de una manera que depende de las longitudes de onda individuales. La luz visible de baja frecuencia (600 nanómetros o más) se refracta en un ángulo más pequeño que la luz de mayor frecuencia, lo que da como resultado un efecto de arco iris, como se ilustra a continuación en la Figura 5.

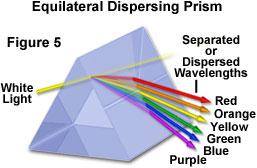
Este mismo fenómeno también es responsable de la aberración cromática. Cuando la luz blanca pasa a través de una lente convexa simple, varios puntos focales surgen en proximidad cercana que corresponden a las diferencias menores del índice de refracción de las longitudes de onda de los componentes. Este efecto tiende a producir halos de colores (rojos o azules, dependiendo del enfoque) que rodean las imágenes de los objetos. La corrección de esta aberración generalmente se logra mediante el uso de combinaciones de dos o más elementos de lentes compuestos de materiales que tienen diferentes propiedades dispersivas, como una lente acromática construida con gafas de corona y de pedernal.

	Interactive Java Tutorial
Refracción por un prisma Examine cómo la luz blanca se separa en sus colores componentes por refracción a través de varios ángulos en un prisma.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. El ejemplo más común es una cámara, que está diseñada para crear imágenes nítidas y enfocadas en una emulsión de película o en la superficie de un dispositivo de acoplamiento de carga (CCD) para producir una imagen precisa. Otros dispositivos ópticos que aprovechan estas características de la luz incluyen microscopios y telescopios, que permiten ver objetos que son invisibles para el ojo humano sin ayuda, independientemente de si están ubicados en la cabeza de un alfiler o en una galaxia distante.

Autores colaboradores

Mortimer Abramowitz – Olympus America, Inc., Two Corporate Center Drive., Melville, Nueva York, 11747.

Shannon H. Neaves y Michael W. Davidson-Laboratorio Nacional de Alto Campo Magnético, 1800 East Paul Dirac Dr., Universidad Estatal de Florida, Tallahassee, Florida, 32310.

VOLVER A LA LUZ Y EL COLOR

¿Preguntas o comentarios? Envíenos un correo electrónico.

© 1998-2021 por Michael W. Davidson y la Universidad Estatal de Florida. Todos los Derechos Reservados. No se pueden reproducir ni utilizar de ninguna manera imágenes, gráficos, scripts o applets sin el permiso de los titulares de los derechos de autor. El uso de este sitio web significa que acepta todos los Términos y Condiciones Legales establecidos por los propietarios.

Este sitio web es mantenido por nuestro
Graphics & Equipo de programación web
en colaboración con Optical Microscopy en el
National High Magnetic Field Laboratory.

Última modificación: Viernes, 13 de noviembre de 2015 a las 02: 18 PM

Número de accesos Desde el 10 de marzo de 2003: 181405

Visite los sitios web de nuestros partners in education: