donde n es el número de muestras individuales, β = 2 cuando se conoce la fase gamética y β = 1 si, en cambio, la fase no se conoce.

Se utilizan varias aproximaciones para inferir la tasa de recombinación utilizando la distancia física (δ) entre dos loci como referencia y traduciéndola en distancia de enlace (d), que generalmente se describe como Mb(δ) ≈ cM(d). Para valores pequeños de d, la última aproximación es válida, pero para valores más grandes de d, la probabilidad de múltiples eventos de recombinación e interferencias aumenta, además, la relación entre la distancia del mapa y la tasa de recombinación no es lineal, ya que la tasa de recombinación máxima posible es de 0,5. Por lo tanto, a menos que se use δ muy corto, la aproximación d ≈ c no es ideal (Corbin et al., 2012). Por lo tanto, implementamos funciones de mapeo para traducir la d estimada en c, siguiendo a Haldane (1919), Kosambi (1943), Sved (1971) y Sved y Feldman (1973). Inicialmente, SNeP infiere d para cada par de SNPs como directamente proporcional a δ de acuerdo con d = kδ, donde k es un valor de tasa de recombinación definido por el usuario (el valor predeterminado es 10-8 como en Mb = cM). El valor inferido de δ se puede someter a una de las funciones de asignación disponibles si el usuario lo requiere.

Resolver la ecuación (3)para Ne e incluir todas las correcciones descritas, permite la predicción de Ne a partir de datos de LD utilizando (Corbin et al., 2012):

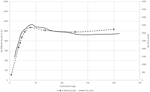
la Figura 1. Comparación de las tendencias Ne de seis razas ovinas suizas según Burren et al. (2014) (líneas discontinuas) y este trabajo (líneas continuas).

El formato requerido para los archivos de entrada es el formato PLINK estándar (ped y archivos de mapa) (Purcell et al., 2007). SNeP permite a los usuarios calcular LD en los datos como se describió anteriormente, o usar una matriz LD precalculada personalizada para estimar Ne usando la Ecuación (5).

La interfaz de software permite al usuario controlar todos los parámetros del análisis, por ejemplo, el rango de distancia entre SNPs en bp, y el conjunto de cromosomas utilizados en el análisis (por ejemplo, 20-23). Además, SNeP incluye la opción de elegir un umbral MAF (predeterminado 0.05), ya que se ha demostrado que la contabilidad de MAF da lugar a estimaciones imparciales de r2, independientemente del tamaño de la muestra (Sved et al., 2008). La arquitectura multihilo de SNeP permite el cálculo rápido de grandes conjuntos de datos (probamos hasta ~100K SNPs para un solo cromosoma), por ejemplo, los datos de BOS descritos aquí se analizaron con un procesador en 2’43», el uso de dos procesadores redujo el tiempo a 1’43», cuatro procesadores redujeron el tiempo de análisis a 1’05».

Ejemplo de cebú

Para el análisis de cebú, las formas de las curvas Ne obtenidas con SNeP y sus tendencias de datos publicados mostraron la misma trayectoria con una disminución suave hasta hace aproximadamente 150 generaciones, seguida de una expansión con un pico hace alrededor de 40 generaciones y que termina en una fuerte disminución en las generaciones más recientes (Figura 1). Sin embargo, si bien las tendencias en ambas curvas fueron las mismas, los dos enfoques dieron lugar a estimaciones de Ne diferentes, con valores de SNeP aproximadamente tres veces mayores que los del documento original. Si bien intentamos utilizar los parámetros de los autores en nuestros análisis, algunas diferencias fueron inevitables, es decir, la publicación original de los datos de ganado estimado r2 con un enfoque diferente al implementado en el SNeP. Los análisis con SNeP se basaron en genotipos, mientras que el análisis original se basó en dos haplotipos de locus inferidos, lo que resulta en los datos publicados que muestran un r2 esperado de 0,32 a la distancia mínima, mientras que nuestras estimaciones fueron de 0,23. Del mismo modo, Mbole-Kariuki et al. (2014) obtuvieron un nivel de fondo r2 = 0.013 alrededor de 2 Mb, mientras que nuestra estimación a la misma distancia fue de 0.0035 (no se muestran los datos). En consecuencia, como nuestras estimaciones de LD fueron consistentemente más pequeñas que Mbole-Kariuki et al. (2014) se espera que nuestras estimaciones de Ne sean mayores. Si bien esta observación pone de relieve la importancia de una elección cuidadosa de los parámetros y sus umbrales, es importante destacar que, aunque la magnitud absoluta de los valores de Ne es diferente, las tendencias son casi idénticas.

Ejemplo de ovejas suizas

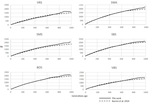
Las seis razas de ovejas suizas analizadas con SNeP produjeron resultados comparables con los del artículo original (Figura 2), con curvas de tendencia Ne en su mayoría superpuestas (Figura 3). Sin embargo, la tendencia general en Ne mostró una disminución hacia el presente. SNeP produjo valores ligeramente mayores de Ne para el pasado más lejano (700-800 generaciones). Esto se debe al diferente sistema de binning utilizado en SNeP, que permite al usuario obtener una distribución más uniforme de comparaciones en pares dentro de cada bin (p. ej., el número de comparaciones de pares SNP dentro de cada bin es comparable). Para el lapso de tiempo que se extiende más allá de hace 400 generaciones, Burren et al. (2014) utilizaron solo tres contenedores en su análisis (centrados en 400, 667 y 2000 generaciones atrás), mientras que para el mismo lapso de tiempo,SNeP utilizó 5 contenedores con una serie de comparaciones en pares que dependen del rango definido con fórmulas 6a, b. En consecuencia, el enfoque de Burren y sus colegas termina con una mayor densidad de datos que describen las generaciones más recientes que los que describen las generaciones más antiguas. Por lo tanto, el uso de menos contenedores tiende a aumentar la presencia de valores más pequeños de Ne en cada contenedor, lo que reduce el valor promedio de Ne para cada contenedor. Los valores de Ne para el pasado reciente, comparados en la generación 29 en el pasado, dieron resultados muy similares. La diferencia más grande (50) se obtuvo para la raza SBS.

la Figura 2. Comparación entre los valores de Ne recientes calculados en la generación 29 en este trabajo y Burren et al. (2014) para seis razas de ovejas suizas.

la Figura 3. Comparación de las tendencias de Ne para las últimas 250 generaciones en los datos de SHZ obtenidos por Mbole-Kariuki et al. (2014) (línea discontinua) y usando SNeP (línea continua).

Discusión

el Análisis de Ne LD utilizando datos se demostró por primera vez hace 40 años, y ha sido aplicado, desarrollado y mejorado desde entonces (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). El número tradicionalmente pequeño de SNPs analizados ya no es una limitación, ya que los chips SNP comprenden un número extremadamente grande de SNPs, disponibles en poco tiempo y a un precio razonable. Esto ha impulsado el uso del método, que se ha aplicado a los seres humanos (Tenesa et al., 2007; McEvoy et al., 2011), así como a varias especies domesticadas (England et al., 2006; Uimari y Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Junto con estas mejoras, las limitaciones metodológicas se han hecho evidentes y se han abordado aquí, y la mayoría de los esfuerzos apuntan a la estimación correcta de Ne recientes. Sin embargo, el valor cuantitativo de la estimación depende en gran medida del tamaño de la muestra, el tipo de estimación de la DL y el proceso de binning (Waples y Do, 2008; Corbin et al., 2012), mientras que su patrón cualitativo depende más de la información genética que de la manipulación de datos.

Hasta el momento, este método se ha aplicado utilizando una variedad de software, no existe un enfoque estandarizado para binarizar los resultados y cada estudio ha aplicado un enfoque más o menos arbitrario, por ejemplo, binning para clases de generación en el pasado (Corbin et al., 2012), binning para clases a distancia con un rango constante para cada bin (Kijas et al., 2012) o compartimentación por clases de distancia de manera lineal, pero con compartimentos más grandes para los puntos de tiempo más recientes (Burren et al., 2014). Hasta donde sabemos, el único software disponible que estima Ne a través de LD es NeEstimator (Do et al., 2014), una versión actualizada del antiguo LDNE (Waples y Do, 2008) que permite el análisis de grandes conjuntos de datos (como SNPChip de 50k). Es importante destacar que, mientras que el SNeP se centra en estimar las tendencias históricas de Ne, el objetivo de NeEstimator es producir estimaciones de Ne imparciales contemporáneas, por lo que estas últimas deben considerarse como una herramienta complementaria al investigar la demografía a través de LD.

Utilizamos SNeP para analizar dos conjuntos de datos en los que el método se aplicó previamente. Los resultados obtenidos para los datos de ovejas fueron tanto cuantitativa como cualitativamente comparables con los obtenidos por Burren et al. (2014), mientras que para los datos de Cebú obtuvimos una estimación de la tendencia Ne que coincidió estrechamente con la de Mbole-Kariuki et al. (2014) aunque nuestras estimaciones puntuales de Ne fueron mayores que las descritas para los datos (Mbole-Kariuki et al., 2014). La discrepancia entre estos dos resultados refleja que Burren y sus colegas produjeron sus estimaciones de r2 utilizando PLINK (el software estándar para la manipulación de datos SNP a gran escala) que utiliza el mismo enfoque utilizado para estimar r2 por SNeP, mientras que Mbole-Kariuki et al. siguió a Hao et al. (2007) for r2 estimation. El uso de diferentes estimaciones para LD es crítico para el aspecto cuantitativo de la curva Ne, donde debido a la correlación hiperbólica entre Ne y r2, una disminución de r2 en su rango más cercano a 0 puede conducir a un cambio muy grande en las estimaciones de Ne, mientras que las diferencias en las estimaciones son menos significativas cuando el valor de r2 es alto, es decir, más cercano a 1. Por lo tanto, aunque en uno de los conjuntos de datos los valores de Ne fueron sustancialmente diferentes, en ambos casos las curvas de Ne se solaparon con las publicadas originalmente.

Como ya han sugerido otros autores, la fiabilidad de las estimaciones cuantitativas obtenidas con este método debe tomarse con precaución, especialmente para los valores de Ne relacionados con las generaciones más recientes y más antiguas(Corbin et al., 2012) porque para las generaciones recientes, están involucrados grandes valores de c, no ajustándose a las implicaciones teóricas que Hayes propuso para estimar una variable Ne a lo largo del tiempo (Hayes et al., 2003). Las estimaciones para las generaciones más antiguas también podrían ser poco fiables, ya que la teoría coalescente muestra que no se puede muestrear de manera confiable ningún SNP después de 4Ne generaciones en el pasado (Corbin et al., 2012). Además, las estimaciones de Ne, y especialmente las relacionadas con generaciones posteriores en el pasado, se ven fuertemente afectadas por factores de manipulación de datos, como la elección de los valores MAF y alfa. Además, la estrategia de compartimentado aplicada puede interferir con la precisión general del método, por ejemplo, cuando se utiliza un número insuficiente de comparaciones en parejas para llenar cada contenedor.

Una de las aplicaciones del método es comparar demografías de razas. En este caso, la forma de las curvas Ne sería la herramienta óptima para diferenciar diferentes historias demográficas, más que sus valores numéricos, usándolas como una huella demográfica potencial para esa raza o especie, sin embargo, teniendo en cuenta que la mutación, la migración y la selección pueden influir en la estimación de Ne a través de LD (Waples y Do, 2010). Además, la consideración cuidadosa de los datos analizados con SNeP (y otro software para estimar Ne) es muy importante, ya que la presencia de factores de confusión como la mezcla, puede resultar en estimaciones sesgadas de Ne (Orozco-terWengel y Bruford, 2014).

El objetivo de SNeP es, por lo tanto, proporcionar una herramienta rápida y confiable para aplicar métodos LD para estimar Ne utilizando datos genotípicos de alto rendimiento de una manera más consistente. Permite dos enfoques de estimación r2 diferentes, además de la opción de usar estimaciones r2 de software externo. El uso de SNeP no supera los límites del método y de la teoría detrás de él, sin embargo, permite al usuario aplicar la teoría utilizando todas las correcciones sugeridas hasta la fecha.

Contribuciones de los autores

MB concibió y escribió el software y el manuscrito. MB, MT y POtW probaron el software y realizaron los análisis. MT, POtW y MWB revisaron el manuscrito. Todos los autores aprobaron el manuscrito final.

Declaración de Conflicto de Intereses

Los autores declaran que la investigación se realizó en ausencia de relaciones comerciales o financieras que pudieran interpretarse como un posible conflicto de intereses.

Agradecimientos

Agradecemos a Christine Flury por proporcionar los datos de las ovejas y por la útil discusión. También agradecemos a los dos revisores sus útiles sugerencias para mejorar este artículo. MB fue apoyado por el programa Master and Back (Regione Sardegna).