Filtros Kalman

El algoritmo utilizado para fusionar los datos se denomina filtro Kalman.

El filtro Kalman es uno de los algoritmos más populares en fusión de datos. Inventado en 1960 por Rudolph Kalman, ahora se usa en nuestros teléfonos o satélites para navegación y rastreo. El uso más famoso del filtro fue durante la misión Apolo 11 para enviar y llevar a la tripulación de regreso a la luna.

¿Cuándo usar un filtro Kalman ?

Se puede usar un filtro Kalman para la fusión de datos para estimar el estado de un sistema dinámico (que evoluciona con el tiempo) en el presente (filtrado), el pasado (suavizado) o el futuro (predicción). Los sensores integrados en vehículos autónomos emiten medidas que a veces son incompletas y ruidosas. La inexactitud de los sensores (ruido) es un problema muy importante y puede ser manejado por los filtros Kalman.

Se utiliza un filtro de Kalman para estimar el estado de un sistema, denotado x. Este vector se compone de una posición p y una velocidad v.

En cada estimación, podemos asociar una medida de la incertidumbre P.

Al realizar una fusión de sensores, hemos de tener en cuenta diferentes datos para el mismo objeto. Un radar puede estimar que un peatón está a 10 metros de distancia, mientras que el Lidar lo estima a 12 metros. El uso de filtros Kalman le permite tener una idea precisa para decidir cuántos metros es realmente el peatón al eliminar el ruido de los dos sensores.

Un filtro Kalman puede generar estimaciones del estado de los objetos a su alrededor. Para hacer una estimación, solo necesita las observaciones actuales y la predicción anterior. El historial de mediciones no es necesario. Por lo tanto, esta herramienta es ligera y mejora con el tiempo.

Cómo luce

el Estado y la incertidumbre están representados por Gaussianas.

Un Gauss es una función continua en virtud de la cual el área es 1. Esto nos permite representar probabilidades. Estamos en una probabilidad de distribución normal. La uni-modalidad de los filtros Kalman significa que tenemos un único pico cada vez para estimar el estado del sistema.

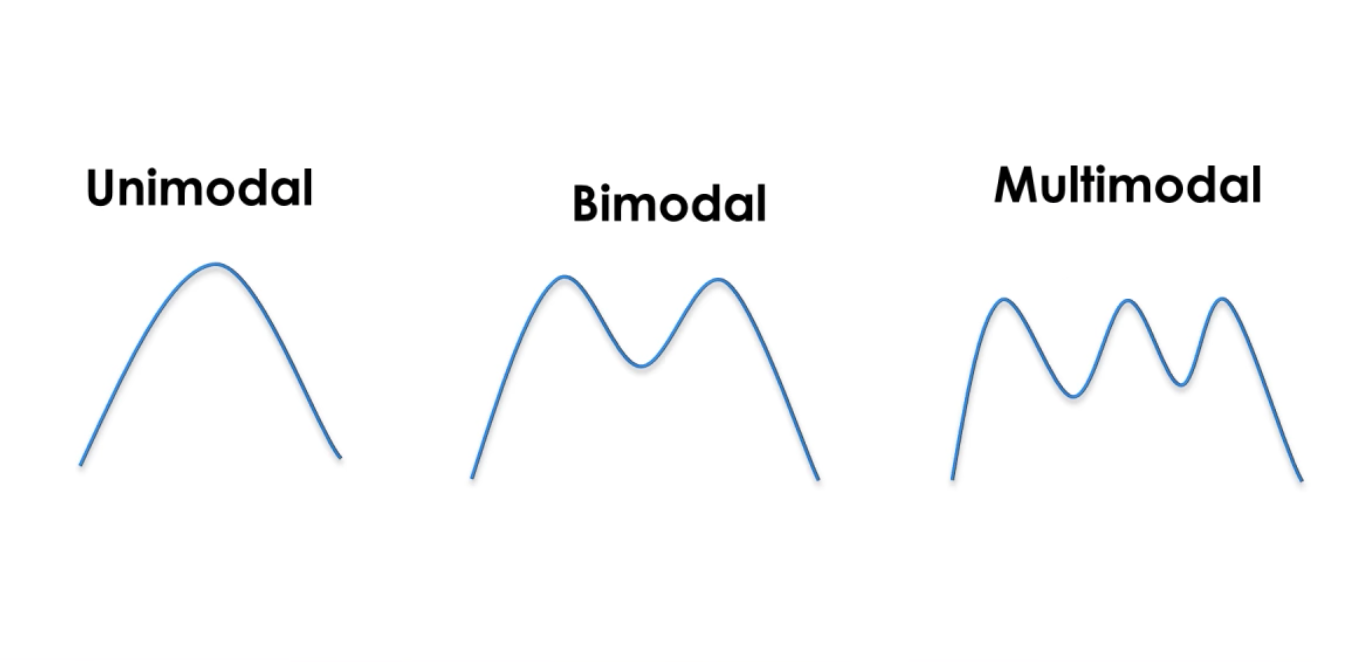
Tenemos una media µ representa un estado y una varianza σ2 que representa una incertidumbre. Cuanto mayor sea la varianza, mayor será la incertidumbre.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Utilizamos las observaciones de nuestros sensores para corregir el estado predicho y obtener una estimación más precisa.

Para hacer una estimación, un filtro Kalman solo necesita observaciones actuales y la predicción anterior. El historial de mediciones no es necesario.

Maths

Las matemáticas detrás de los filtros Kalman están hechas de adiciones y multiplicaciones de matrices. Tenemos dos etapas: Predicción y Actualización.

Predicción
Nuestra predicción consiste en estimar un estado x’ y una incertidumbre P ‘ en el tiempo t de los estados anteriores x y P en el tiempo t-1.

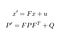
• F: La matriz de transición de t-1 a t
• ν: el Ruido añadido
• Q: Matriz de covarianza que incluye ruido

Actualización
La fase de actualización consiste en utilizar una medición z de un sensor para corregir nuestra predicción y, por lo tanto, predecir x y P.

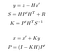
• y: Diferencia entre la medición real y la predicción, es decir, el error.
• S: Error estimado del sistema
• H: Matriz de transición entre el marcador del sensor y el nuestro.
• R: Matriz de covarianza relacionada con el ruido del sensor (dada por el fabricante del sensor).
• K: Kalman gain. Coeficiente entre 0 y 1 que refleja la necesidad de corregir nuestra predicción.

La fase de actualización permite estimar una x y una P más cerca de la realidad de lo que proporcionan las mediciones.

Un filtro Kalman permite realizar predicciones en tiempo real, sin datos de antemano. Utilizamos un modelo matemático basado en la multiplicación de matrices para cada tiempo definiendo un estado x (posición, velocidad) e incertidumbre P.

Représentation Prior / Posterior

Este diagrama muestra lo que sucede en un filtro Kalman.

• estado de predicción estimación representa nuestra primera estimación, nuestra fase de predicción. Estamos hablando de prior.
• La medición es la medición de uno de nuestros sensores. Tenemos mejor incertidumbre, pero el ruido de los sensores hace que sea una medición que siempre es difícil de estimar. Hablamos de probabilidad.
• La estimación del estado óptimo es nuestra fase de actualización. La incertidumbre es esta vez la más débil, acumulamos información y permitimos generar un valor más seguro que con nuestro sensor solo. Este valor es nuestra mejor suposición. Hablamos de posterior.

Lo que implementa un filtro de Kalman es en realidad una regla de Bayes.

En un filtro de Kalman, nos bucle de predicciones a partir de las mediciones. Nuestras predicciones son siempre más precisas, ya que mantenemos una medida de incertidumbre y calculamos regularmente el error entre nuestra predicción y la realidad. Podemos, a partir de multiplicaciones de matrices y fórmulas de probabilidad, estimar velocidades y posiciones de vehículos a nuestro alrededor.

Filtros»extendidos/Sin perfume» y no linealidad

Surge un problema esencial. Todas nuestras fórmulas matemáticas se implementan con funciones lineales de tipo y = ax + b.
Un filtro Kalman siempre funciona con funciones lineales. Por otro lado, cuando usamos un Radar, los datos no son lineales.

El Radar ve el mundo con tres medidas:

Estos tres valores hacen que nuestra medición sea no lineal dada la inclusión del ángulo φ.

Nuestro objetivo aquí es convertir los datos ρ, φ, ρ a datos cartesianos (px, py, vx, vy).

Si ingresamos datos no lineales en un filtro Kalman, nuestro resultado ya no está en forma gaussiana unimodal y ya no podemos estimar la posición y la velocidad.

Así que el uso de aproximaciones, que es por eso que estamos trabajando en dos métodos:
– Extendido de Kalman filtros de uso de Jacobina y la serie de Taylor para linealizar el modelo.
– Los filtros Kalman sin perfume utilizan una aproximación más precisa para linealizar el modelo.

Para hacer frente a la inclusión de la no linealidad por el Radar, existen técnicas que permiten a nuestros filtros estimar la posición y velocidad de los objetos que deseamos rastrear.