Antenas irradian energía Electromagnética para transmitir o recibir información. Por lo tanto, los términos Energía y Potencia están asociados con estas ondas electromagnéticas y tenemos que discutirlas. Una onda electromagnética tiene campos eléctricos y magnéticos.

Considere la onda en cualquier instante, que se puede ver en ambos vectores. La siguiente figura muestra la representación de componentes eléctricos y de campos magnéticos en una onda electromagnética.

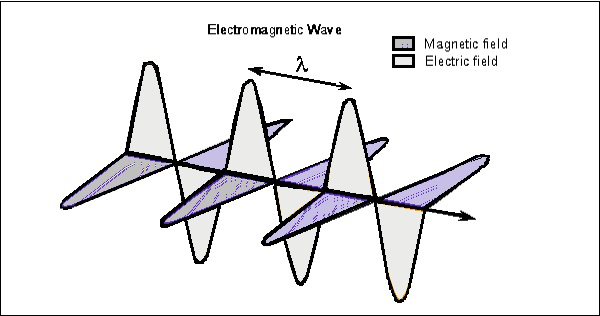
La onda eléctrica está presente vertical a la propagación de la onda EM, mientras que la onda magnética está ubicada horizontalmente. Ambos campos están en ángulo recto entre sí.

Vector de Poynting

El vector de Poynting describe la energía de la onda EM por unidad de tiempo por unidad de área en cualquier instante de tiempo dado. John Henry Poynting derivó por primera vez este vector en 1884 y por lo tanto fue nombrado en su honor.

Definición – «El vector de Poynting da la velocidad de transferencia de energía por unidad de área»

o

«La energía que lleva una onda por unidad de tiempo por unidad de área viene dada por el vector de Poynting.»

El vector de Poynting está representado por Ŝ.

Unidades

La unidad SI del vector de Poynting es W / m2.

Expresión matemática

La cantidad que se usa para describir la potencia asociada con las ondas electromagnéticas es el vector de Poynting instantáneo, que se define como

\\hat{S} = \hat{E} \times\hat{H}Donde

• \ \ hat{S} is es el vector de Poynting instantáneo (W/m2).

• \ \ hat{E} is es la intensidad instantánea del campo eléctrico (V / m).

• \ \ hat{H} is es la intensidad instantánea del campo magnético (A/m).

El punto importante a tener en cuenta aquí es que la magnitud de E es mayor que H dentro de una onda EM. Sin embargo, ambos aportan la misma cantidad de energía. Ŝ es el vector, que tiene dirección y magnitud. La dirección de Ŝ es la misma que la velocidad de la onda. Su magnitud depende de E y H.

Derivación del Vector de Poynting

Para tener una idea clara del vector de Poynting, pasemos por la derivación de este vector de Poynting, en un proceso paso a paso.

Imaginemos que una Onda EM, pasa un área (A) perpendicular al eje X a lo largo del cual viaja la onda. Al pasar a través de A, en tiempo infinitesimal (dt), la onda viaja una distancia (dx).

$$dx = C\ dt$$

Donde

$$C = velocidad\ de\ la luz = 3\times 10^{8}m/s$$$$volumen, dv = Adx = AC\ dt$$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$$= \epsilon_{0} AC \ E^{2}\ dt$$

por lo Tanto, la Energía que se transfiere en el tiempo (dt) por área (A) es −

$$S = \frac{Energía}{Tiempo\times Área} = \frac{ps}{dt\ A} = \frac{\epsilon_{0}AS^{2}\ dt}{dt\ A} = \epsilon_{0}C\:E^{2}$$

Ya

$$\frac{E}{H} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \, a continuación,\ S= \frac{CB^{2}}{\mu_{0}}$$

Ya

$$C = \frac{E}{H} \, a continuación, \ S = \frac{EB}{\mu_{0}}$$$$= \hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Ŝ denota el vector de Poynting.

La ecuación anterior nos da la energía por unidad de tiempo, por unidad de área en cualquier instante de tiempo dado, que se llama vector de Poynting.