La Teoría Revolucionaria de Galois

El 31 de mayo de 1832, un revolucionario republicano francés llamado Évariste Galois murió de un disparo. Tenía 20 años. La noche anterior, temiendo su propia muerte, Galois había escrito muchas cartas, garabateando frenéticamente «No tengo tiempo; no tengo tiempo». Una carta es particularmente valiosa por razones históricas. En esta carta, Galois afirma haber desencadenado la revolución. No una política. Pero uno matemático.
La revolución iniciada por Galois resultó ser más grande y profunda de lo que él podría haber imaginado! El panorama de las matemáticas se ha visto profundamente afectado por la visión de Galois, ya que su progenie ha crecido y se ha apoderado del mundo matemático. Esta progenie es ahora omnipresente y gobierna tierras ilimitadas. Se llama álgebra pura.
Para romantizar un poco más la narración de la vida dramática de Galois, aquí hay un resumen de un documental que hice sobre álgebra:

¡Definitivamente lo es! Pero su revolución matemática no fue fácil. Como todo líder de la revolución, primero tuvo las mayores dificultades. No para imaginar la revolución. Pero para convencer a otros de que se unan a él en un enfoque revolucionario de las matemáticas. Cuando Galois aún estaba vivo, sus ideas revolucionarias fueron rechazadas varias veces por la academia de ciencias francesa Because ¡Porque los mejores matemáticos franceses de la época, como Siméon Denis Poisson, no podían entenderlas! En parte debido a la escritura ilegible de Galois que se muestra a la derecha
En 1843, 10 años después de la muerte de Galois, finalmente, un brillante matemático francés llamado Joseph Liouville logró captar algunas de las ideas de Galois. Después de 3 años más de trabajo, Liouville publicó un artículo para explicarlos. Pero el artículo de Liouville todavía era demasiado descabellado para que otros matemáticos lo disfrutaran y entendieran. Tomó otros 24 años para encontrar un matemático francés lo suficientemente sobresaliente como para comprender mejor a Galois y hacer que sus ideas sean límpidas. Esta matemática sobresaliente es Camille Jordan. De hecho, el libro de Jordan de 1870 sobre la teoría de Galois estaba tan bien escrito que el matemático alemán Felix Klein lo encontró tan legible como un libro alemán.
Definitivamente fue un gran impulso. Pero tomaría otros 82 años para que el gran matemático austriaco Emil Artin finalmente diera a la teoría de Galois su forma moderna, en 1942. Artin merece muchos créditos. Mientras que Galois fue el visionario que previó esta revolución, Artin, en muchos sentidos, es el que realmente emprendió la revolución y volcó las matemáticas. Gracias a Artin, y a algunos otros, hoy en día, la teoría de Galois se ha convertido en una piedra angular inevitable de la investigación en matemáticas, con muchos logros sorprendentes y sorprendentes (como la prueba de Wiles del último teorema de Fermat), ¡así como una enorme reserva de preguntas abiertas y misterios!
Campos en Álgebra pura
La teoría de Galois trata de simetrías de números. Pero antes de llegar allí, necesito presentarte para armarte al contarte un secreto sobre números. Y estoy seguro de que has oído hablar de él! De hecho, en la escuela secundaria, probablemente te enseñaron a no dejar raíces en los denominadores.
Quiero decir que $1 / (\sqrt{2}-1) was no fue una respuesta correcta. ¿Puede ayudar a deshacerse de la raíz cuadrada de 2 en el denominador?
Jeje He Nos enseñaron a multiplicar arriba y abajo por el conjugado del denominador. Este conjugado se obtiene mediante la sustitución $-$ por $+$ (o viceversa) en el denominador:
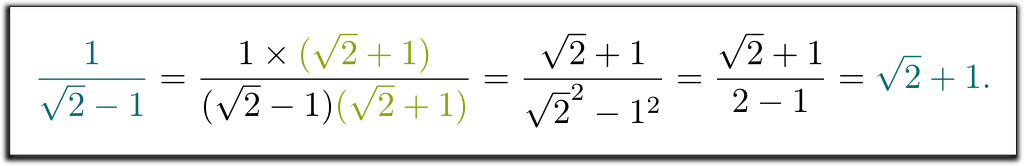
¡Lo sé! La complicada expresión $1/(\sqrt{2}-1)$ representa el mismo número que $\sqrt{2}+1$. Y esto explica por qué nuestros profesores querían que escribiéramos los resultados de una manera en lugar de la otra: Cuando todo está escrito de la misma manera, ¡los exámenes se vuelven mucho más fáciles de corregir!
Pero ¿qué pasa con $1 / (\sqrt{2}-1)?? ¿Puedes deshacerte de la raíz en el denominador? ¿Se puede hacer?
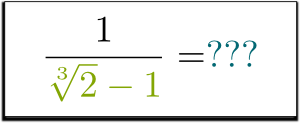
¡Lo sé!
¡Dímelo tú!
un poco de suerte?
Jeje Interestingly Curiosamente, cualquier potencia de $\sqrt{2}-1 can se puede escribir como una suma de potencias de$ \sqrt{2}.. De hecho, solo necesita distribuir los productos:
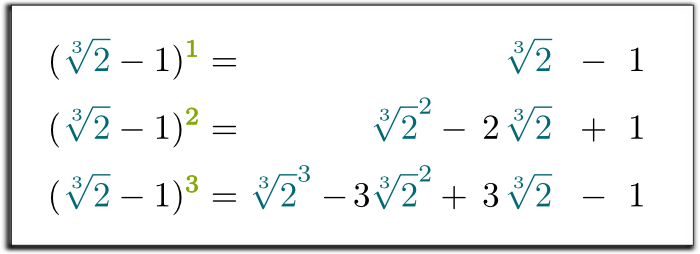
¡Sí, lo es! Al hacer esta sustitución en la tercera ecuación, hemos demostrado que las tres primeras potencias de $\sqrt{2}-1$ puede ser escrita como una suma de un número racional, de $\sqrt{2}$ y $\sqrt{2}^2$!
Así que ahora tenemos 3 ecuaciones, ¡con 2 expresiones raíz queremos deshacernos de ellas! Por lo tanto, podemos combinar las ecuaciones para eliminar todas las expresiones raíz de la derecha.
Multiplicemos las 2 primeras líneas por 3 y sumemos las 3 ecuaciones:
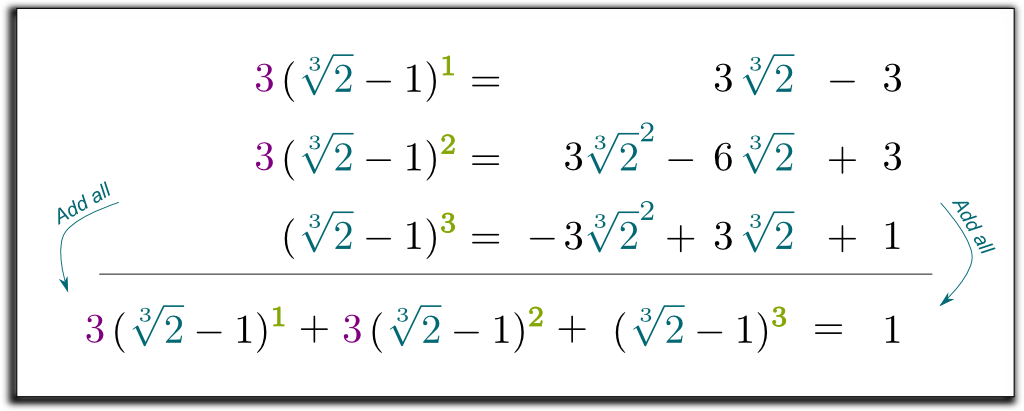
Jeje He Lo bueno es que el término izquierdo que hemos obtenido ahora se puede factorizar con $\sqrt{2}-1!! Déjame saltar algunas aburrido cálculos… Y llegar al resultado $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Por lo tanto, para deshacerse de las raíces en el denominador, podemos multiplicar hacia arriba y hacia abajo por \\sqrt{2}^2 + \ sqrt{2} + 1!! Finalmente, obtenemos la siguiente fórmula sorprendente y hermosa:
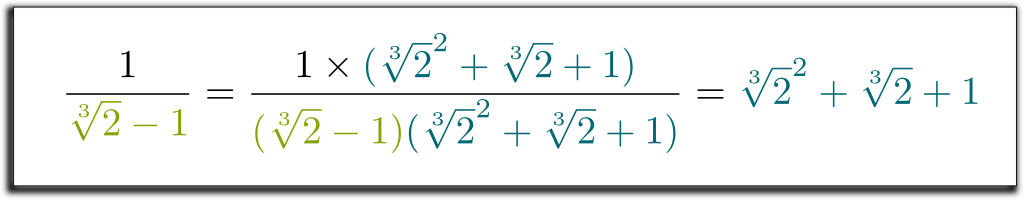
¡Lo sé! ¡Pero lo que es aún más ordenado es que el método que usamos es muy general! Con técnicas similares, ahora podemos eliminar todos los radicales de los denominadores.
Ahora, lo que era de particular interés para Galois no era el hecho de que un método permitiera eliminar radicales de denominadores. Pero más bien, que cualquier número con radicales en denominadores equivalía a un número con radicales en la parte superior. Esto significaba que los números con radicales en la parte superior eran estables por división.
Es común denotar $\mathbb Q{2}] the el conjunto de números que se puede escribir como una suma de potencias de$ \sqrt{2}.. Desde $\sqrt{2}^3 = 2$ es un número racional, cualquier suma de las potencias de $\sqrt{2}$, de hecho, puede ser escrita en la forma estándar a $\sqrt{2}^2 + b\sqrt{2} + c$. Ahora, si sumamos, restamos o multiplicamos dos números cualquiera, entonces no es difícil ver que obtenemos números que todavía se pueden poner en la forma estándar a a\sqrt{2}^2 + b\sqrt{2} + c.. Además, lo que acabamos de mostrar aquí es que el inverso de todos los números a a\sqrt{2}^2 + b\sqrt{2} + c also también se puede escribir en forma estándar. Esto muestra que cualquier suma, resta, multiplicación y división de números en \ \ mathbb Q{2}] yields produce un número, que se puede escribir en forma estándar belongs y, por lo tanto, pertenece a$ \mathbb Q{2}].. En términos de álgebra pura, $\mathbb Q{2}] is es así estable por las cuatro operaciones aritméticas clásicas. Por esta razón, lo llamamos un campo.
Geometría de extensiones de campo
El campo con el que está más familiarizado es probablemente el conjunto Q\mathbb Q of de números racionales. Otros ejemplos de campos son los conjuntos \\mathbb R of de números reales y el conjunto \ \ mathbb C of de números complejos. Y ahora, también tenemos $\mathbb Q{2}]$. Desde $\mathbb Q{2}]$ es un campo que contiene el campo $\mathbb Q$, decimos que $\mathbb Q{2}] / \mathbb P$ es un campo de extensión.
El hecho de que $\mathbb Q{2}] / \mathbb Q is sea una extensión de campo produce una conexión muy natural entre los dos campos. Es decir, $\mathbb Q{2}] can se puede ver como un espacio vectorial, donde $\mathbb Q is es el campo escalar. En particular, el hecho de que cualquier número en $\mathbb Q{2}]$ puede ser escrito $a \sqrt{2}^2 + b\sqrt{2} + c$ significa que $(1, \sqrt{2}, \sqrt{2}^2)$ conforma una base de $\mathbb Q{2}]$ como $\mathbb Q$-espacio vectorial. ¡Y esto significa que podemos representarlo geométricamente como un espacio de 3 dimensiones!
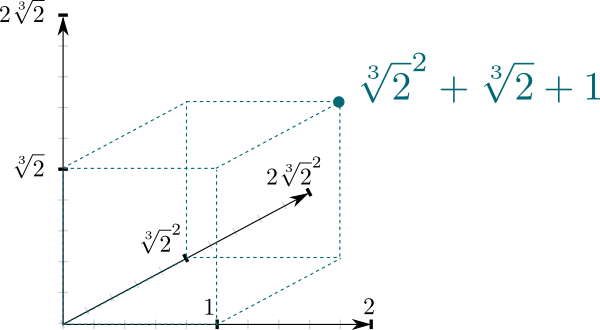
La dimensión del espacio vectorial de arriba es una propiedad interesante de las extensiones de campo. Se conoce como el grado, y comúnmente se denota \\big{2}]:\mathbb Q \ big] = 3 for por ejemplo.
¡Sí! En realidad, es bastante fácil crear una extensión de campo de esto: Simplemente agregue un número radical que no pertenezca a \ \ mathbb Q{2}]!!
¡Sí! Esto crearía el campo $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$. Estos campos contienen todos los números que son productos y sumas de $\sqrt{2} and y $\sqrt{2}.. Estos son de la forma $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. ¿Alguna idea de cuál es el grado \\big{2}, \sqrt{2}]:\mathbb Q{2}] \ big] is?
¡Sí! De hecho, tenemos a $\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e \sqrt{2} + f) \sqrt{2}$. Por lo tanto, cualquier cantidad de $\mathbb Q{2},\sqrt{2}]$ puede ser escrito $A+B\sqrt{2}$, donde $A$ y $B$ pertenecer a $\mathbb Q{2}]$. Así, 2 escalares de $\mathbb Q{2}] determine determinan un número en $\mathbb Q{2},\sqrt{2}].. Esto significa que el grado de extensión del campo \\mathbb Q{2}, \sqrt{2}] / \ mathbb Q{2}] is es 2. De hecho, tenemos la relación de Chasles $\big{2}, \sqrt{2}] : \mathbb Q \big] $=$ \big{2}, \sqrt{2}] : \mathbb Q{2}] \big] \big{2}] : \mathbb Q \big] $=$ 2 \times 3 = 6$.
¡Es mejor que eso! Cualquier extensión de campo de grado finito, llamada extensión de campo finito, se extiende por un solo número. Por ejemplo, $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, lo que significa que todos los números, que son las sumas de las potencias de $\sqrt{2}$ y $\sqrt{2}$ son también las sumas de las potencias de $\sqrt{2} + \sqrt{2}$. ¿No es sorprendentemente impresionante?
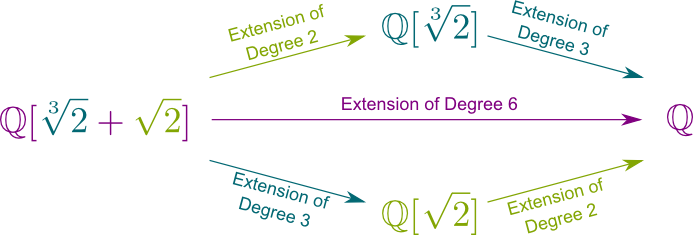
de manera Más general, cualquier campo finito de extensión de $\mathbb Q$ puede ser escrito $\mathbb Q$ unos $x$, que es añadido a $\mathbb Q$.
Sí. Es el caso de la extensión de campo $\mathbb R/\mathbb Q$. ¡Y también lo es la extensión de campo más importante en la teoría de Galois! Esta extensión de campo es $ \ bar {\mathbb Q} / \mathbb Q Q, donde $ \ bar {\mathbb Q} is es el conjunto de números algebraicos. Estas son todas las soluciones de ecuaciones polinómicas de la forma $a_n x^n $+$ a_{n-1} x^{n-1} $+$ … $+$ a_1 $ x+$ a_0 = 0$. Por ejemplo, $\sqrt{2} is es un número algebraico porque es la solución a $x^4-2x = 0$. Por lo tanto, $\bar{\mathbb Q} is es una extensión de campo para todas las extensiones de campo finitas de$ \mathbb Q..
Números conjugados
¡Casi hemos llegado! Necesitamos un desvío final a través de ecuaciones polinómicas.

¡Exactamente! Galois notó que algunas ecuaciones podían simplificarse. Por ejemplo, $x^4-2x=0$ pueden ser factorizados como $x(x^3-2)=0$, lo que corresponde a $x=0$ o $x^3-2=0$. Así, la ecuación $x^4-2x=0$ se puede reducir a ecuaciones de $x=0$ y $x^3-2=0$. Y de hecho, esta reducción es muy similar a cómo números como 35 se pueden reducir a 5 y 7, porque 5 5 \por 7 = 35$. La similitud entre ecuaciones y números enteros es tan fuerte que incluso podemos hacer divisiones euclidianas de polinomios, ¡al igual que aprendiste a hacerlo para números! A la derecha hay un ejemplo de tal división (no te preocupes si no la entiendes, no será importante para la secuela).
¡Exactamente! Se conocen como ecuaciones polinómicas irreducibles. La ecuación^x ^ 3-2= 0 is es un ejemplo de ecuación polinómica irreducible.
¡Sí! Pero, fundamentalmente, Galois quería centrarse en ecuaciones con coeficientes racionales. O, mejor dicho, polinomios con coeficientes que pertenecen al campo base. Entonces, lo que quise decir fue que, para $\mathbb Q as como el campo base,$ x^3-2=0 is es irreducible.
Consideremos $x^2-2x -1 = 0 have para tener algunas pistas. Se puede demostrar que esta ecuación es irreductible. ¿Recuerdas cómo resolverlo?
Si $b^2 – 4ac \ geq 0 0, sí.
¡Exactamente! Así, el polinomio irreducible de la ecuación $x^2 + 2x -1=0$ tiene dos soluciones: $1+\sqrt{2}$ y $1-\sqrt{2}$… Cualquier comentario?
¡Bingo! Ese es el descubrimiento clave de Galois. Más generalmente, Galois llamado conjuga todas las soluciones a una ecuación polinómica irreducible. Y, como se puede imaginar, ¡estos son esenciales para eliminar los radicales de los denominadores!
La primera cosa a notar es que, si $x_1$, $x_2$, …, $x_n$ son todas las soluciones de un polinomio irreducible de la ecuación de $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$, con coeficientes racionales, entonces este polinomio irreducible ecuación en realidad puede ser reescrito $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Al identificar los términos constantes, se obtiene $x_1 x_2 x x_n = = ^(-1) ^ n a_0/a_n.. Así que, de manera crucial, el producto de los números conjugados es el número racional^(-1) ^ n a_0 / a_n$, que es distinto de cero (¡pruébalo!).
Aquí hay una pequeña broma para tener en cuenta la fuerte conexión entre conjugados:

Considere una fracción $1 / x_1 where, donde $x_1 is es una expresión complicada con radicales. Multiplicando arriba y abajo por los conjugados $x_2$, …, $x_n$ de $x_1$, a continuación, los rendimientos de $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, que no tiene radical en el denominador como hemos establecido $a_0$ a ser un número distinto de cero de la base de campo!
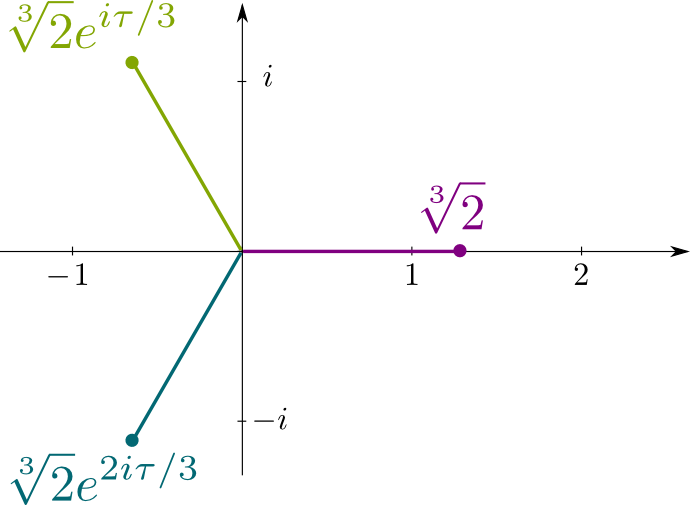
Recuerde que $x^3-2= 0 is es la ecuación polinómica irreducible \ \ sqrt{2} is es la solución de. Por lo tanto, sus conjugados son las soluciones a la ecuación, que son los números complejos $\sqrt{2}j$ y $\sqrt{2}j^2$, donde $j= e^{i\tau/3}$ con $\tau = 2\pi$ ser la razón de la circunferencia de un círculo por su radio. La siguiente figura muestra las ubicaciones de las soluciones conjugadas en este plano complejo:
Ambigüedad de Galois
Finalmente, ¡llegamos a la visión clave de Galois!
Los conjugados son perfectamente permutables. Esto significa que, si cambia sistemáticamente $\sqrt{2} by por su conjugado$- \sqrt{2}$, entonces las igualdades aún se mantienen. Por ejemplo, desde que tenía $1/(\sqrt{2}-1) = \sqrt{2}+1$, puedo directamente decirle que $1/(-\sqrt{2}-1)=-\sqrt{2}+1$! Del mismo modo, tenemos la siguiente implicación impresionante:
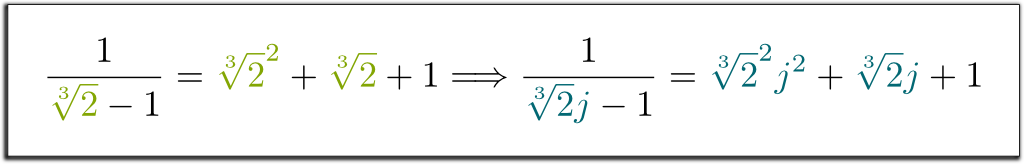
Jeje Let Permítanme recordar primero que los campos finitos se extienden por un solo elemento. Por lo tanto, si el campo base es de $\mathbb Q$, cualquier campo finito puede ser escrito $\mathbb Q$ para algún derecho $x_1$. Ahora, tenga en cuenta que $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ irreducible ecuación polinómica $x_1$ es la solución. Entonces, lo que define a $\mathbb P$ es $\mathbb Q$-espacio vectorial generado por $x_1$, $x_1^2$, …, $x_1^{n-1}$, con la simplificación de los mayores poderes de $x_1$ de acuerdo a la regla algebraica $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.
¡Exactamente! Fundamentalmente, estas reglas algebraicas de $\mathbb Q$, en realidad, no dependen de la naturaleza de $x_1$; sólo dependen de la polinomio irreducible $x_1$ es la solución! Por lo tanto, las reglas de $\mathbb Q$ son idénticos a estos de $\mathbb Q$, …, $\mathbb Q$, donde $x_1$ es sustituido por uno de sus conjugados $x_2$, …, $x_n$. En particular, los campos \ \ mathbb Q{2}] and y \ \ mathbb Q{2} j] operate funcionan de acuerdo a las mismas reglas. ¡Por eso los conjugados son perfectamente permutables! Podemos decir que los campos de $\mathbb Q{2}]$ y $\mathbb Q{2} j]$ son isomorfos, y que la sustitución de $\sqrt{2}$ en $\sqrt{2}j$ es un isomorfismo $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.
De una manera muy similar (pero más fuerte) que dos espacios vectoriales de dimensión 2 son más o menos lo mismo! Esto tiene consecuencias terribles. Significa que, desde una perspectiva algebraica, no tiene sentido hacer una diferencia entre un número y cualquiera de sus conjugados (siempre y cuando reemplaces sistemáticamente el número por su conjugado). Así, por ejemplo, $\sqrt{2}$ y $-\sqrt{2}$ son algebraicamente indistinguible! Para tener esto en cuenta, aquí hay otro chiste que se me ocurrió:

¡Para nada! Cualquier distinción entre estos dos números debe involucrar otras matemáticas además del álgebra, como las relaciones de orden o la topología. Lo que quiero decir es que, por ejemplo, la relación $\sqrt{2} > 0$ hace una diferencia entre $\sqrt{2}$ en $-\sqrt{2}$, pero eso es porque se trata de un orden de relación. Pero si nos limitamos a igualdades polinómicas, entonces no hay absolutamente ninguna diferencia entre $\sqrt{2}. y$- \sqrt{2}.. Del mismo modo, $i$ e $-i$, las soluciones del polinomio irreducible ecuación $x^2+1=0$, también son algebraicamente indistinguibles. Sin embargo, llamamos arbitrariamente i yo one a uno de ellos. Es por eso que Galois llamó a su teoría la teoría de la ambigüedad. Hoy en día, la ambigüedad de la elección de los convencionales de la raíz cuadrada de $-1$ entre $i$ e $-i$ es el lugar llamado la simetría entre $i$ e $-i$.
Los grupos de Galois
Galois se enfocaron particularmente en extensiones de campo que son estables por conjugación. Estas extensiones de campo estables ahora se conocen como extensiones de Galois. Por lo tanto, si $x_1$ pertenece a una extensión de Galois, entonces este Galois de la extensión contiene todos sus conjugados $x_2$, …, $x_n$.
Una forma sencilla de construir extensiones de Galois consiste en tomar el campo atravesado por soluciones de una ecuación polinómica irreducible. Por ejemplo, si $x_1$, …, $x_n$ son conjugados para el campo base $\mathbb Q$, entonces $\mathbb Q / \mathbb P$ es una extensión de Galois. Los campos construidos de esta manera se llaman campos de división.
Por ejemplo, la división de campo de la ecuación $x^3-2=0$ es la extensión de Galois $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ se extendió por sus soluciones.
Si $x_1 spans abarca una extensión de Galois, entonces también lo hacen sus conjugados. Por lo tanto, $\mathbb Q = \mathbb Q =$ … $=\mathbb Q$ = $\mathbb Q$. Por lo tanto, el isomorfismo entre $\mathbb P$ y $\mathbb Q$, que consiste en la sustitución de $x_1$ por $x_2$ es, de hecho, un isomorfismo entre $\mathbb Q$ y sí! Lo llamamos automorfismo. Automorfismos de una extensión de Galois $\mathbb Q/\mathbb Q$ formas el grupo de Galois $Gal(\mathbb Q/\mathbb Q)$.
Ahora, fundamentalmente, si $\mathbb Q = \mathbb Q$, entonces todos los automorfismos de una extensión de Galois $\mathbb Q/ \mathbb Q$ son permutaciones de $x_1$, con una de sus conjugados! En particular, vemos aquí que la cardinalidad de un grupo de Galois es igual al grado de la extensión de Galois.
¡Claro! Usted puede notar que $\mathbb Q = \mathbb P$ y $\mathbb Q = \mathbb Q$, lo que significa que $i$ y $\sqrt{2}$ cada una abarca la división de los campos de la irreductible ecuación polinómica que son solución de. Por lo tanto, $\mathbb Q/\mathbb Q are y both\mathbb Q/\mathbb Q are son extensiones de Galois. Por lo tanto, su automorfismos consistir en la sustitución de $i$ por uno de sus conjugados, $i$ o $-i$, y la sustitución de $\sqrt{2}$ en $\sqrt{2}$ o $-\sqrt{2}$. En los primeros casos, no estamos cambiando nada a números, que corresponde a la simetría cero. Los segundos casos se pueden visualizar como simetrías axiales, como se muestra en la siguiente figura:

¿No es increíble?
¡Claro! Vayamos al campo de división \ \ mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] of de$ x^3-2=0.. Pero, antes de continuar, vamos a notar que $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.
Todo lo que necesitamos probar es que todos los generadores de un campo pertenecen al otro. Comencemos por demostrar que los generadores de este último, $\sqrt{2} {y j j belong, pertenecen al primero. Es obvio para $\sqrt{2}$. Ahora, $j = (\sqrt{2} j) / \sqrt{2}$, por lo tanto $j belong también pertenece al campo anterior. Esto demuestra que todos los elementos de $\mathbb Q{2},j]$ pertenecer a $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Recíprocamente, es sencillo, que todos los generadores de la ex campo, $\sqrt{2}$, $\sqrt{2}j$ y $\sqrt{2}j^2$, son productos de los generadores de este último. Por lo tanto, ambos campos son iguales. Y, en particular, $\mathbb Q{2}, j] / \mathbb Q is es una extensión de Galois.
Jeje He Para entender las simetrías de $\mathbb Q{2}] need, necesitaremos ir más lejos en el estudio de Galois de los grupos de Galois Correspondence
Correspondencia de Galois
El problema con los grupos de Galois es que pueden volverse extremadamente grandes y complicados. Este es particularmente el caso del grupo infinito Gal Gal (\bar{\mathbb Q}/\mathbb Q)$. Para aprehender grupos tan grandes y complejos, Galois tuvo la brillante idea de romperlos en pedazos más pequeños.
Sorprendentemente, Galois descubrió que los grupos de Galois se podían dividir en subgrupos de simetrías solo mirando aquellos que dejan algún subcampo sin cambios. Por ejemplo, $\mathbb Q is es un subcampo de $\mathbb Q{2}, j]$, ya que cualquier número del primero pertenece al segundo. Por lo tanto, las simetrías de $\mathbb Q{2},j]$ que no cambie nada para $\mathbb Q$ forman un subgrupo del grupo de Galois de $\mathbb Q{2},j]/\mathbb Q$. Estas simetrías forman el grupo de Galois Gal Gal (\mathbb Q{2}, j] / \mathbb Q)$.
¡Lo sé! Me gusta visualizar estas simetrías como formas de conectar $\mathbb Q{2},j] onto a$ \mathbb Q.. Aquí hay una imagen de la «conexión»:
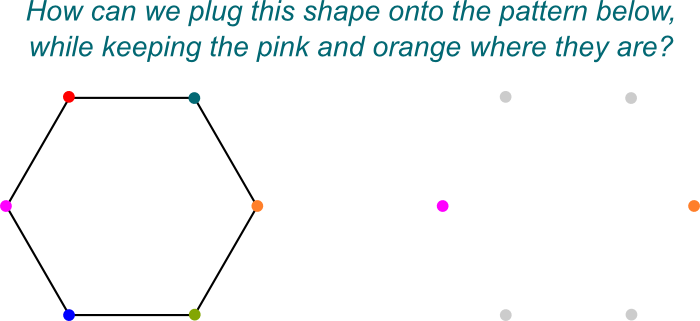
¡Exactamente! Y eso es simplemente porque $\mathbb Q{2},j]$ es una extensión de Galois de $\mathbb Q$, que es en sí mismo un campo de extensión de $\mathbb Q$.
¡Y hay más! Galois mostró que todos los subgrupos de extensiones de Galois se obtienen de esta manera. Más precisamente, la asignación de cualquier campo $K$ entre el Galois de la extensión de $\mathbb Q{2},j]$ y el campo base $\mathbb Q$ a el grupo de Galois $Gal(\mathbb Q{2},j] / K)$ es bijective. ¡Este hecho se llama la correspondencia de Galois! Esta correspondencia se muestra esquemáticamente a continuación para una extensión de Galois $\mathbb Q/\mathbb Q$.

En lugar de intentar describir este grupo directamente, centrémonos en su subgrupo Gal Gal (\mathbb Q{2}, j] / \mathbb Q).. Es sencillo que $\sqrt{2}$ se extiende $\mathbb Q{2},j]$ cuando se añade a $\mathbb Q$. Por lo tanto, $\mathbb Q{2}, j]/\mathbb Q is es una extensión de Galois abarcada por$ \sqrt{2}.. Por lo tanto, el uso de un teorema que hemos visto anteriormente, sabemos que todos los automorfismos de este Galois de la extensión consiste en la sustitución de $\sqrt{2}$ por uno de sus 3 conjugados (sí, $\sqrt{2} j$ y $\sqrt{2} j^2$)!
Ahora, podría seguir estudiando otras piezas de $Gal (\mathbb Q{2}, j]/\mathbb Q) like, como el subgrupo de Galois Gal Gal(\mathbb Q{2},j]/\mathbb Q{2}])). Pero prefiero usar otro de los poderosos teoremas de Galois. Es decir, demostró que, si $\mathbb Q/\mathbb Q$ era, además, una extensión de Galois, entonces el subgrupo de $Gal(\mathbb Q{2}, j]/\mathbb Q)$ es normal.
Por lo tanto,el grupo de Galois de $\mathbb Q{2}, j]/\mathbb Q can puede ser cocido por este subgrupo, y el grupo cociente entonces es igual a$ Gal(\mathbb Q/\mathbb Q) Q. Sin embargo, $\mathbb Q/\mathbb P$ es de hecho una extensión de Galois se extendió por $j$, cuyo conjugado es $j^2$. Por lo tanto, $Gal(\mathbb Q/\mathbb Q)$ consiste en dejar $j$ como $j$ o sustituirlo con $j^2$.
ahora podemos deducir todas las simetrías de la $Ga(\mathbb Q{2},j]/\mathbb Q)$ mediante la combinación de estos de la $Ga(\mathbb Q{2},j] / \mathbb Q)$ y $Gal(\mathbb Q/\mathbb Q)$. Podemos mostrar estas simetrías por el dibujo de cómo afectan a nuestros tres que abarca conjugados $\sqrt{2}$, $\sqrt{2}j$ y $\sqrt{2}j^2$:
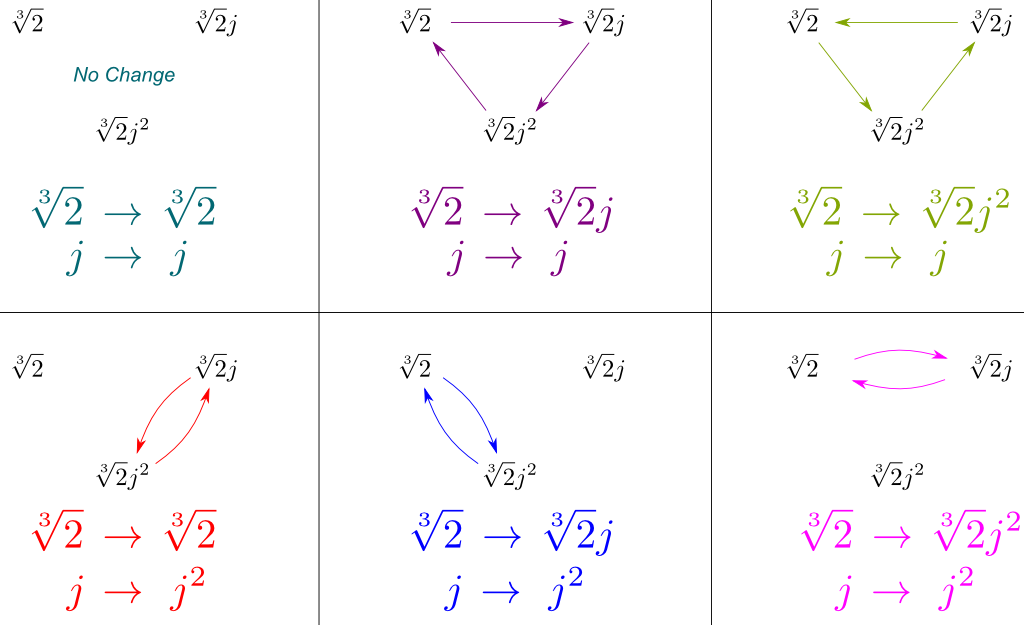
Fundamentalmente, la figura de arriba contiene todas las simetrías de $Gal (\mathbb Q{2},j]/\mathbb Q)$. Y sorprendentemente, estas simetrías corresponden a un grupo bien conocido de simetría.
Entonces, ¿las simetrías aquí son como una estrella de mar o como un triángulo?
¡Sí, de hecho! Este grupo de simetrías del triángulo se llama $D_3$, y es el mismo que el grupo de $S_3$ de permutaciones de 3 elementos. Esto nos lleva a la siguiente fórmula, que me pareció tan hermosa, que he decidido enmarcarla.
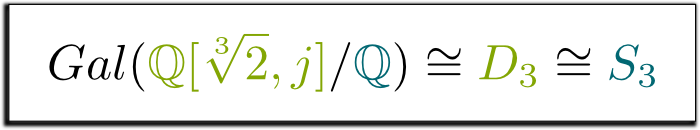
Concluyamos
En muchos sentidos, Galois debe ser considerado como el padre del álgebra moderna. Su visión clave fue mirar las matemáticas a través del ángulo de las reglas de operaciones, y esto lo llevó a desvelar ambigüedades sorprendentes y perspicaces, o simetrías, entre los números. A partir de una expresión algebraica perspectiva, los números como $\sqrt{2}$, $\sqrt{2}j$ y $\sqrt{2}j^2$ son, de hecho, perfectamente simétrica y totalmente intercambiables.
La comprensión de estas simetrías ha tenido aplicaciones sorprendentes en geometría algebraica y topología algebraica, entre otras. En particular, los primeros éxitos de la teoría incluyen una clasificación de polígonos regulares construibles y un teorema que afirma que las ecuaciones polinómicas de alto grado no pueden ser resueltas por radicales.
Los éxitos recientes aparecen en criptografía y en la prueba de Andrew Wiles del último teorema de Fermat. Esta prueba implica estudiar el grupo de Galois Gal Gal (\bar{\mathbb Q} /\mathbb Q) with con representación de grupo. Pero yo diría que la teoría es de alguna manera todavía joven, y queda mucho por descubrir. Después de todo, es una de las áreas de investigación más activas en la investigación matemática pura de hoy en día.
Esto debería llevarnos a rendir muchos más homenajes al increíble genio de Galois Let permítanme incluir uno de SocraticaStudios.