Prealgebra
Resultados de Aprendizaje
- Encontrar el área de la base y la altura de un triángulo
- Encontrar la longitud de un lado de un triángulo dados el perímetro y otros dos longitudes
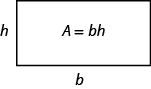
ahora sabemos cómo encontrar el área de un rectángulo. Podemos usar este hecho para ayudarnos a visualizar la fórmula para el área de un triángulo. En el rectángulo de abajo, hemos etiquetado la longitud b y el ancho h, por lo que su área es bh.
El área de un rectángulo es la base, b, por la altura, h.
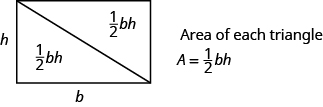
Podemos dividir este rectángulo en dos triángulos congruentes (vea la imagen de abajo). Los triángulos que son congruentes tienen longitudes y ángulos laterales idénticos, por lo que sus áreas son iguales. El área de cada triángulo es la mitad del área del rectángulo, o \frac{1}{2}bh. Este ejemplo nos ayuda a ver por qué la fórmula para el área de un triángulo es A = \frac{1}{2} bh.
Un rectángulo se puede dividir en dos triángulos de igual área. El área de cada triángulo es la mitad del área del rectángulo.
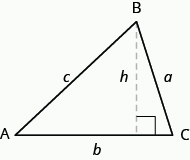
La fórmula para el área de un triángulo es A=\frac{1}{2}bh, donde b es la base y h es la altura.Para encontrar el área del triángulo, necesita saber su base y altura. La base es la longitud de un lado del triángulo, generalmente el lado de la parte inferior. La altura es la longitud de la línea que conecta la base con el vértice opuesto, y forma un ángulo \text{90}^ \circ con la base. La imagen de abajo muestra tres triángulos con la base y la altura de cada uno marcados.
La altura h de un triángulo es la longitud de un segmento de línea que conecta la base con el vértice opuesto y crea un ángulo \text{90}^ \circ con la base.

Propiedades del triángulo
Para cualquier triángulo \ Delta ABC, la suma de las medidas de los ángulos es \text{180}^ \circ.
m \ angle{A}+m \ angle {B}+m \ angle {C} = 180^\circ
El perímetro de un triángulo es la suma de las longitudes de los lados.
P=a+b+c
El área de un triángulo es la mitad de la base, b, de la altura, h.
A=\frac{1}{2}bh
ejemplo
Busque el área de un triángulo cuya base es de 11 pulgadas y cuya altura es de 8 pulgadas.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétala con la información dada. | 
|
| Paso 2. Identifique lo que está buscando. | el área del triángulo |
| Paso 3. Nombre. Elija una variable para representarla. | sea a = área del triángulo |
| Paso 4.TRADUCIR.
Escriba la fórmula apropiada. Sustituir. |
 |
| Paso 5. Resuelve la ecuación. | A=44 pulgadas cuadradas. |
| Paso 6. Comprobar:
A = \frac{1}{2}bh 44\stackrel{?}{=}\frac{1}{2}(11)8 44=44\marca de verificación |
|
| Paso 7. Responde la pregunta. | El área es de 44 pulgadas cuadradas. |
intentarlo
ejemplo
El perímetro de un jardín triangular es de 24 pies. Las longitudes de dos lados son de 4 pies y 9 pies. ¿Cuánto dura el tercer lado?
intentarlo
ejemplo
El área de un triángulo de la iglesia de la ventana es de 90 metros cuadrados. La base de la ventana es de 15 metros. ¿Cuál es la altura de la ventana?
intentarlo
Isósceles y Triángulos Equiláteros
Además de la derecha, triángulo, algunos otros triángulos tienen nombres especiales. Un triángulo con dos lados de igual longitud se llama triángulo isósceles. Un triángulo que tiene tres lados de igual longitud se llama triángulo equilátero. La siguiente imagen muestra ambos tipos de triángulos.
En un triángulo isósceles, dos lados tienen la misma longitud, y el tercer lado es la base. En un triángulo equilátero, los tres lados tienen la misma longitud.
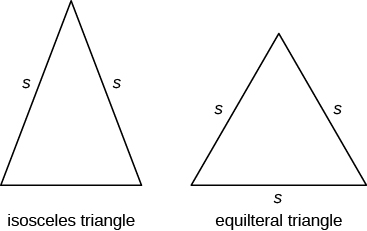
Isósceles y triángulos equiláteros
Un triángulo isósceles tiene dos lados de la misma longitud.Un triángulo equilátero tiene tres lados de igual longitud.
ejemplo
El perímetro de un triángulo equilátero es de 93 centímetros. Encuentra la longitud de cada lado.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. La bufanda será un triángulo isósceles con una base de
60 pulgadas. ¿Cuánto tiempo puede hacer los dos lados iguales?








