Una parte integral de la dinámica de fluidos es la vorticidad. Heurísticamente, mide la rotación local de una parcela fluida. Para los objetos sólidos no hablamos de la vorticidad de un objeto, sino que nos referimos a su velocidad angular. Estos dos conceptos están relacionados, pero la vorticidad es más útil cuando se discuten objetos rotativos que se deforman, como lo hace un fluido.

La vorticidad de un campo de velocidad dado dentro de un plano dado, se calcula eligiendo dos ejes ortogonales cualesquiera en ese plano y agregando la velocidad angular de cada eje. En un objeto sólido, o un fluido que gira como un objeto sólido (acertadamente llamado rotación del cuerpo sólido), la vorticidad es el doble de la velocidad angular, ya que cada eje gira a la misma velocidad. Sin embargo, en un fluido, los dos ejes pueden girar a velocidades muy diferentes e incluso en direcciones diferentes. Incluso es posible que cada eje pueda girar, pero la vorticidad neta es cero (ver vórtice irrotacional).

Si el movimiento de un fluido está estrictamente confinado a permanecer en un plano, el vector de vorticidad se toma como ortogonal al plano y no puede cambiar de dirección (o inclinación). El único aspecto de la vorticidad que puede cambiar es su magnitud. Se cree que esta transferencia de energía a escalas más grandes está conectada con la formación de la Gran Mancha Roja en Júpiter.

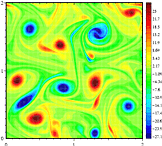
En movimiento fluido tridimensional, el vector de vorticidad es tridimensional, ya que tiene componentes paralelos a cada eje, x, y y z: el componente z es paralelo al eje z y describe la velocidad de rotación en el plano xy. Es debido a esta dicotomía que hay una diferencia cualitativa en el comportamiento entre la turbulencia bidimensional y la turbulencia tridimensional. En el primero hay una tendencia a que los vórtices se agrupen y formen vórtices más grandes, mientras que en el segundo los movimientos vórtices se separan y la energía cae en cascada a las escalas más pequeñas donde luego se difunde.

Matemáticamente, la vorticidad de un determinado campo de velocidad,

se define para ser el rizo de la velocidad, y generalmente se denota con la letra griega omega,

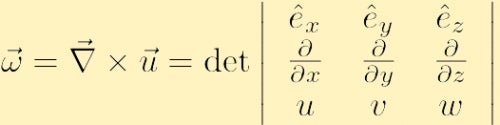
donde hemos utilizado la convencional nabla símbolo para el degradado:

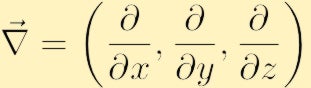
En forma de componentes de la vorticidad se encuentra expandiendo el determinante anterior,

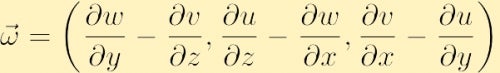
Otro aspecto importante de la dinámica de fluidos que está relacionada con la vorticidad es la circulación. A diferencia de la vorticidad, que es una propiedad local, definida en cada punto del espacio, la circulación es una propiedad global, definida mediante la integración de una propiedad del fluido sobre una curva. En particular, si elige cualquier contorno cerrado y lo denota con la letra C(t), la circulación alrededor de C(t), en sentido contrario a las agujas del reloj, es una cantidad escalar denotada con,

se define como,

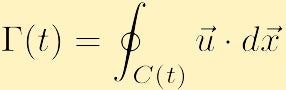
que puede ser una función del tiempo, al igual que el contorno cerrado.

Tomemos un momento para explicar lo que esto está diciendo físicamente. En cada punto del Contornoc(t) encontramos la componente de la velocidad que es tangente a la curva y multiplicamos este escalar por una longitud infinitesimal; proyectar la velocidad en la tangente necesariamente dará una magnitud entre la velocidad en esa posición y cero. Si la velocidad es tangente a la curva, obtenemos más o menos la velocidad de, si la velocidad es ortogonal a la curva, obtenemos cero. Luego integramos esta cantidad, una forma diferente de decir sumando un número infinito de cosas, alrededor del contorno para agregar la contribución de cada punto. A partir de esto, determinamos que la circulación a lo largo de un contorno C(t) es la cantidad de flujo alrededor del contorno C (t); un resultado positivo o negativo corresponde a la circulación de contorno en el sentido de las agujas del reloj o en el sentido de las agujas del reloj, respectivamente. Un caso extremo es donde el campo de velocidad está en todas partes perpendicular a la curva C(t) y, en consecuencia, no hay circulación, ya que el flujo siempre cruza el contorno y nunca fluye a lo largo del contorno. Para obtener una circulación distinta de cero, debe haber alguna parte de la curva donde el flujo esté a lo largo del contorno cerrado.

Si el campo de velocidad es suave y no hay singularidades dentro de C (t), entonces podemos usar el Teorema Integral de Stokes del cálculo vectorial para reescribir la circulación como,

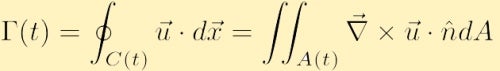
donde A es el área contenida dentro del contorno C y â es el vector normal unitario a la areaA.

Antes de contemplar esta nueva ecuación para la circulación, es útil entender el significado físico del Teorema de Stokes donde el campo vectorial es la velocidad. En la integral doble anterior calculamos la vorticidad en cada punto dentro del contorno y luego sumamos la vorticidad sobre todos estos puntos en A(t). En la integral única sobre el contorno cerrado estamos calculando el flujo a lo largo del límite del área. El teorema de Stokes establece que estas cantidades son iguales, y por lo tanto que si hay vorticidad media dentro de un área, lo que debe significar que el área tiene una tasa de rotación distinta de cero, por lo tanto, debe haber una circulación neta a lo largo del perímetro de ese límite.

A partir del Teorema del Valor Medio del cálculo, podemos reemplazar el integrando en la integral doble por un valor medio, que corresponde al componente medio de la vorticidad ortogonal al plano en el que se encuentra C(t). Por lo tanto, la segunda interpretación de la circulación es que es la vorticidad media por el área contenida dentro de C(t). En lugar de calcular la circulación en el contorno cerrado C(t), podemos calcular la vorticidad media normal a A(t) y multiplicarla por el área interior. Si se considera el caso especial en el que la vorticidad es constante en todas partes, la circulación sería la magnitud de la vorticidad por el área contenida dentro.

Un vórtice de punto es un vórtice que no tiene área, lo que significa que la vorticidad está presente solo en un único punto. Para estudiar los vórtices puntuales, primero asumiremos que tenemos un flujo incompresible 2D. (Los vórtices de punto también se conocen a veces como vórtices de línea cuando se ven en 3D.)

Después de algunos cálculos, determinamos que el campo de velocidad generado por un vórtice de punto, en forma compleja, que se encuentra en z0 está dado por (donde Gamma cero es la circulación alrededor del vórtice de punto, que a menudo se conoce como la fuerza del vórtice de punto):

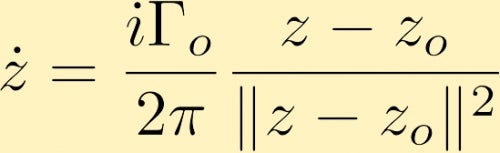
El campo de velocidad generado por un vórtice de punto puede hacer que otro vórtice de punto se mueva. Aquí hay algunos ejemplos de esto: Los vórtices de dos puntos, tanto positivos como de igual magnitud, los vórtices de dos puntos, ambos positivos, pero uno tiene el triple de la fuerza del otro y un vórtice de punto es negativo con el doble de la magnitud del otro que es positivo . Otra posibilidad es considerar dos vórtices de punto de la misma magnitud pero signo opuesto.

Esto se puede extender a cualquier número de vórtices de puntos, N. La ecuación de movimiento en forma compleja para un vórtice de puntos alfa viene dada por:

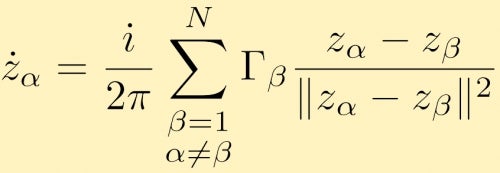
Observar las interacciones de los vórtices de puntos es un problema muy interesante que es difícil de hacer analíticamente, especialmente a medida que aumenta el número de vórtices de puntos. Por lo tanto, las simulaciones numéricas de interacciones de vórtices puntuales son muy comunes. Una aplicación útil de las simulaciones de vórtices de puntos grandes es si nos fijamos en grandes grupos de vórtices de puntos que simulan vórtices con área finita. Aquí están las descripciones y los resultados de varias simulaciones de vórtices de puntos grandes. En este caso tenemos dos grandes grupos de vórtices de puntos de fusión de igual fuerza. En el siguiente caso comenzamos con un anillo de veracidades de puntos agrupados.

Para encontrar una ecuación para la evolución de la vorticidad comenzamos con la ecuación del momento. En la ecuación de momento, el término advectivo se puede reescribir de la siguiente manera,

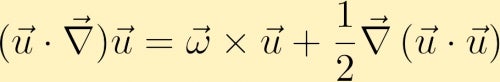
A continuación calculamos el rizo de la ecuación de momento y, a través de algunas identidades vectoriales, obtenemos la ecuación de vorticidad:

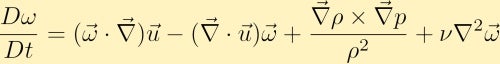
La ecuación de vorticidad muestra cómo se puede generar vorticidad en un fluido. Sin pérdida de generalidad asumiremos que inicialmente solo tenemos vorticidad en la dirección z. A partir de esto podemos ver cómo cada uno de los cuatro términos diferentes puede alterar la vorticidad.

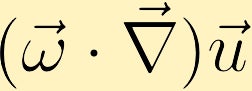
Si hay un cambio en la velocidad con la dirección de la vorticidad existente, se puede generar vorticidad.

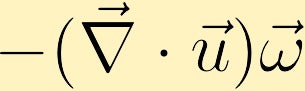
Si una parcela de fluido se está expandiendo y la vorticidad es positiva, la vorticidad de la parcela de fluido disminuirá y si la parcela se contrae, la vorticidad aumentará.

capas de Fluido de densidad constante (isopycnals) quiere coincidir con capas de presión constante (las isobaras). Si estas capas no coinciden, el fluido comienza a girar para alinearlas, lo que provoca que se genere vorticidad. (En el ejemplo empezamos con cero vorticidad.)

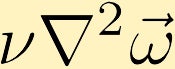
Las fuerzas viscosas causan la difusión de la vorticidad. (En el ejemplo comenzamos con un punto de vorticidad infinita en el centro.)