digitaalisen maailman aikakaudella näemme suosituksen joka osa-alueella sää se on sähköisen kaupankäynnin verkkosivuilla tai viihde verkkosivuilla tai sosiaalisen verkoston sivustoja. Suositus ei ainoastaan anna käyttäjälle sen suositeltua valintaa (perustuen aikaisempaan toimintaan), vaan se kertoo myös käyttäjän käyttäytymisestä (sentimentaalinen analyysi tai emotion AI).

joten ensin selvitetään, mikä suositus on. Se on pohjimmiltaan suositella kohde käyttäjälle perustuu sen menneisyyden haku / toimintaa.

kuva 1 kertoo Amazonin suosituksesta, joka perustuu aiempaan selaushistoriaan ja aiempiin hakuihin. Niin, voimme sanoa, että suositus on pohjimmiltaan ennustaa tulevaa käyttäytymistä perustuu aiempaan käyttäytymiseen. Suositusjärjestelmässä

1 – Sisältöpohjainen suodatus

2 – yhteistoiminnallinen suodatus

Sisältöpohjainen suodatus-

Sisältöpohjainen suodatus-

se perustuu ajatukseen kohteen suosittelemisesta käyttäjälle K: lle, joka on samanlainen kuin aikaisempi K: N Hyvin luokittelema kohde.sisältöpohjaisen suodatuksen peruskäsite on TF — IDF (Term frequency-inverse document frequency), jota käytetään dokumentin / sanan / elokuvan jne. merkityksen määrittämiseen. Sisältöpohjainen suodatus osoittaa suosituksessa läpinäkyvyyttä, mutta toisin kuin yhteistoiminnallinen suodatus, se ei voi toimia tehokkaasti suurten tietojen

yhteistoiminnallinen suodatus

se perustuu ajatukseen, että ihmiset, jotka jakavat saman kiinnostuksen tietyntyyppisiin kohteisiin, jakavat saman kiinnostuksen myös toisentyyppisiin kohteisiin toisin kuin sisältö, joka perustuu metatietoon, kun se käsittelee tosielämän toimintaa. Tämäntyyppinen suodatus on joustava suurin osa verkkotunnuksen (tai voimme sanoa, että se on verkkotunnuksen vapaa) mutta koska kylmä käynnistys ongelma, tietojen harvuus (joka hoidettiin matriisi factorization) tämäntyyppisen algoritmin edessä joitakin takaisku joissakin skenaariossa.

Matrix factorization

Matrix factorization tulee parrasvaloihin Netflix-kilpailun (2006) jälkeen, kun Netflix ilmoitti 1 miljoonan dollarin palkintorahasta niille, jotka parantavat sen root mean square-suorituskykyä 10%. Netflix tarjosi koulutustietoja 100 480 507 arvioinnista, jotka 480 189 käyttäjää antoi 17 770 elokuvalle.

Matriisifaktorointi on kollaboratiivinen suodatusmenetelmä, jossa matriisi m*n hajotetaan m*k: ksi ja k*n: ksi . Sitä käytetään periaatteessa kompleksimatriisioperaation laskemiseen. Jako matriisi on sellainen, että jos me kerrotaan factorized matriisi saamme alkuperäisen matriisin kuten kuvassa 2. Sitä käytetään kahden entiteetin välisten piilevien piirteiden löytämiseen (voidaan käyttää useampaa kuin kahta entiteettiä, mutta tämä tulee tensorikertoimen piiriin)

matriisin hajoaminen voidaan luokitella kolmeen tyyppi-

1 – LU hajoaminen — matriisin hajoaminen L-ja U-matriisiksi, jossa L on alempi kolmiomatriisi ja U on ylempi kolmiomatriisi, jota käytetään yleensä lineaarisen regressiokertoimen löytämiseen. Tämä hajoaminen epäonnistui, jos matriisi ei ole voinut hajota helposti

2 – QR – matriisin hajoaminen-matriisin hajoaminen Q: ksi ja R: ksi, jossa Q on neliömatriisi ja R on ylempi kolmiomatriisi (ei välttämätön neliö). Käytetään eigen system analysis

3 – Kolesky Decomposition – tämä on enimmäkseen käytetty hajoaminen koneoppimisessa. Lineaarisen pienimmän neliösumman laskemiseen lineaarista regressiota

Matriisifaktorointia voidaan käyttää eri aloilla, kuten kuvantunnistus, suositus. Matrix käytetään tämän tyyppinen ongelma ovat yleensä harvassa, koska on mahdollista, että yksi käyttäjä saattaa arvostella vain joitakin elokuvia. Matriisifaktorisoinnille on olemassa erilaisia sovelluksia, kuten Dimensionaalisuuden vähentäminen (jos haluat tietää enemmän dimensionaalisuuden vähentämisestä, katso Dimensionaalisuuden kirous), piilevän arvon hajoaminen

Ongelmalauseke

taulukossa 1 on 5 käyttäjää ja 6 elokuvaa, joissa jokainen käyttäjä voi arvostella minkä tahansa elokuvan. Kuten voimme nähdä, että Henry ei arvioinut Thor ja Rocky samoin Jerry ei arvio Avatar. Reaalimaailman skenaariossa nämä matriisityypit voivat olla erittäin harvoja matriiseja

ongelmalauseemme on, että joudumme selvittämään luokittelemattomien elokuvien luokitukset taulukon 1 mukaisesti

tavoitteenamme on löytää käyttäjän luokitus matriisitehtävien perusteella, mutta sitä ennen joudumme käymään läpi yksikköarvon hajoamisen (SVD), koska matriisitekijät ja SVD liittyvät toisiinsa

SVD: n ja matriisin factorisointi

ennen SVD: n syvyyteen menoa katsotaan ensin, mikä on K ja transponoidaan(K). Jos suoritamme PCA matriisi K (Taulukko 1) saamme kaikki käyttäjän vektori. Myöhemmin voimme laittaa nämä vektorit matriisin U sarakkeeseen ja jos suoritamme PCA: n transposoimalla(K) saamme kaikki elokuvavektorit, joista tulee matriisin m sarake

joten sen sijaan, että suorittaisimme PCA: n k: lle ja transposoisimme(k) erikseen, voimme käyttää SVD: tä, joka voi suorittaa PCA: n k: lle ja transposoida(k) yhdellä otoksella. SVD on periaatteessa factorisoitu matriisi K matriisiin U, matriisiin M ja diagonaalimatriisiin:

missä k on alkuperäinen matriisi, u on käyttäjämatriisi,m on elokuvamatriisi ja keskimmäinen on diagonaalimatriisi

yksinkertaisuuden vuoksi voimme poistaa diagonaalimatriisin joksikin aikaa niin Uusi yhtälö tulee:

Let R is rating defined for user U and item I, P on rivi m käyttäjälle ja Q on sarake transpose(u) for a specific item I. SO yhtälö tulee:

Huomautus — Jos k on tiheän matriisin arvo kuin M on K*transposition eigenvektori(K), samoin u: n arvo on transposition eigenvektori(k)*k mutta meidän matriisimme on harva matriisi, emme voi laskea U: ta ja M: ää tällä lähestymistavalla

joten tässä tehtävämme on löytää Matrix m ja U . Yksi tapa on alustaa satunnaisarvo M: lle ja U: lle ja verrata sitä alkuperäiseen matriisiin K, jos arvo on lähellä K: ta, kuin lopettaa menettely muuten minimoimalla U: n ja M: n arvo, kunnes ne ovat lähellä K: ta . Tällaisen optimoinnin prosessia kutsutaan gradient descentiksi

joten perustehtävämme on minimoida keskimääräinen neliövirhefunktio, joka voidaan esittää :

As our main task is to minimize the error i.e. meidän on löydettävä, mihin suuntaan meidän on mentävä, että meidän on erotettava se, joten uudeksi yhtälöksi tulee

/div>

div>

näin ollen P: n ja U: n päivitetty arvo tulee nyt:

Where alpha is learning rate generally its value is very small as higher alpha can overshoot the minimum value.

Regularization in Recommendation

When we fit the model to the training data it returns some decision line . Kyseisen päätösrivin perusteella voidaan erottaa tietojen jakauma

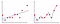
kuvassa 2 ensimmäisessä kuviossa malli on asennettu lineaarisesti, kun taas toisessa kuviossa se on varustettu polynomiasteella. Ensi silmäyksellä näyttää siltä, että Toinen tontti on paljon parempi kuin ensimmäinen tontti, koska se antaa 99% tarkkuuden koulutustietoihin, mutta mitä jos otamme käyttöön testitiedot ja se antaa 50% tarkkuuden testitietoihin . Tämäntyyppisiä ongelmia kutsutaan ylilatauksiksi ja ongelman voittamiseksi otamme käyttöön käsitteen nimeltä Regularisointi.

koska ylisuuruusongelma on yleinen koneoppimisessa, on olemassa kahdentyyppinen säännönmukaistamismenetelmä, jolla voidaan poistaa ylisuuruus

1 – L1 – säännönmukaistaminen

2-L2-säännönmukaistaminen

L1-säännönmukaistaminen lisää kertoimen lineaarista suuruutta rangaistustermiksi, kun taas L2: ssa lisätään kertoimen neliösuuruus häviöfunktioon / virhefunktioon (kuten edellä). L1 palaa harvakseltaan matriiseja, kun taas L2 ei. L1 Regularisointi toimii hyvin ominaisuuksien valinnassa harvassa matriisissa.

suositusaineistossa on myös suuri todennäköisyys, että tietoja päätyy liikaa. Joten, poistaa overfitting ongelma voimme lisätä L2 regularization (koska matriisi on jo harva emme tarvitse L1 regularization täällä)vuonna tappio funktio siten Uusi yhtälö tappio funktio on:

taas voimme löytää gradientin päivitetystä MSE: stä ja saada päivitettyjä pisteitä noudattamalla samaa lähestymistapaa kuin edellä on käsitelty

yksi tärkeä asia, joka on otettava huomioon yllä olevassa skenaariossa matriisi P ja Q ovat ei-negatiivisia, joten näitä factorization-tyyppejä kutsutaan myös ei-negatiivisiksi factorizationeiksi. Koska ei-negatiivinen factorization automaattisesti poimii tietoa ei-negatiivinen joukko vektorin. NMF: ää käytetään laajalti kuvankäsittelyssä, tekstinlouhinnassa, suuriulotteisen tiedon analysoinnissa