Blog
Dans un article de blog précédent, nous avons discuté de la façon dont les supermarchés utilisent les données pour mieux comprendre les besoins des consommateurs et, en fin de compte, augmenter leurs dépenses globales. L’une des techniques clés utilisées par les grands détaillants est appelée Analyse du panier de marché (MBA), qui permet de découvrir les associations entre les produits en recherchant des combinaisons de produits qui se produisent fréquemment dans les transactions. En d’autres termes, cela permet aux supermarchés d’identifier les relations entre les produits que les gens achètent. Par exemple, les clients qui achètent un crayon et du papier sont susceptibles d’acheter un caoutchouc ou une règle.
« L’analyse du panier de marché permet aux détaillants d’identifier les relations entre les produits que les gens achètent. »
Les détaillants peuvent utiliser les informations tirées du MBA de plusieurs façons, notamment:
- Regrouper les produits qui se produisent conjointement dans la conception de l’agencement d’un magasin pour augmenter les chances de vente croisée;
- Piloter des moteurs de recommandation en ligne (« les clients qui ont acheté ce produit ont également consulté ce produit » »; et
- Ciblant les campagnes marketing en envoyant des coupons promotionnels aux clients pour les produits liés aux articles qu’ils ont récemment achetés.
Compte tenu de la popularité et de la valeur du MBA, nous avons pensé produire le guide étape par étape suivant décrivant son fonctionnement et la manière dont vous pourriez entreprendre votre propre analyse du panier de marché.
Comment fonctionne l’analyse du Panier de marché?
Pour effectuer un MBA, vous aurez d’abord besoin d’un ensemble de données de transactions. Chaque transaction représente un groupe d’articles ou de produits qui ont été achetés ensemble et souvent appelés « ensemble d’articles ». Par exemple, un ensemble d’articles peut être: {crayon, papier, agrafes, caoutchouc} auquel cas tous ces articles ont été achetés en une seule transaction.
Dans un MBA, les transactions sont analysées pour identifier les règles d’association. Par exemple, une règle pourrait être : {pencil, paper}= > {rubber}. Cela signifie que si un client a une transaction qui contient un crayon et du papier, il est susceptible d’être intéressé par l’achat d’un caoutchouc.
Avant d’agir sur une règle, un détaillant doit savoir s’il existe suffisamment de preuves pour suggérer que cela entraînera un résultat bénéfique. Nous mesurons donc la force d’une règle en calculant les trois mesures suivantes (notez que d’autres mesures sont disponibles, mais ce sont les trois plus couramment utilisées) :
Support : le pourcentage de transactions qui contiennent tous les éléments d’un ensemble d’éléments (par exemple, crayon, papier et caoutchouc). Plus le support est élevé, plus le jeu d’éléments se produit fréquemment. Les règles avec un support élevé sont préférées car elles sont susceptibles d’être applicables à un grand nombre de transactions futures.
Confiance: la probabilité qu’une transaction qui contient les éléments du côté gauche de la règle (dans notre exemple, crayon et papier) contienne également l’élément du côté droit (un caoutchouc). Plus la confiance est élevée, plus la probabilité que l’article du côté droit soit acheté est grande ou, en d’autres termes, plus le taux de retour auquel vous pouvez vous attendre pour une règle donnée est élevé.
Ascenseur: la probabilité que tous les éléments d’une règle se produisent ensemble (autrement appelé support) divisée par le produit des probabilités des éléments du côté gauche et du côté droit se produisant comme s’il n’y avait aucune association entre eux. Par exemple, si le crayon, le papier et le caoutchouc se produisaient ensemble dans 2,5% de toutes les transactions, le crayon et le papier dans 10% des transactions et le caoutchouc dans 8% des transactions, alors l’ascenseur serait: 0.025/(0.1*0.08) = 3.125. Une levée de plus de 1 suggère que la présence de crayon et de papier augmente la probabilité qu’un caoutchouc se produise également dans la transaction. Dans l’ensemble, lift résume la force de l’association entre les produits à gauche et à droite de la règle; plus la lift est grande, plus le lien entre les deux produits est grand.
Pour effectuer une analyse du panier de marché et identifier les règles potentielles, un algorithme d’exploration de données appelé « algorithme Apriori » est couramment utilisé, qui fonctionne en deux étapes:
- Identifier systématiquement les ensembles d’éléments qui se produisent fréquemment dans l’ensemble de données avec un support supérieur à un seuil pré-spécifié.
- Calculez la confiance de toutes les règles possibles compte tenu des ensembles d’éléments fréquents et ne conservez que celles dont la confiance est supérieure à un seuil pré-spécifié.
Les seuils auxquels définir le support et la confiance sont spécifiés par l’utilisateur et sont susceptibles de varier d’un ensemble de données de transaction à l’autre. R a des valeurs par défaut, mais nous vous recommandons de les expérimenter pour voir comment elles affectent le nombre de règles renvoyées (plus d’informations ci-dessous). Enfin, bien que l’algorithme Apriori n’utilise pas lift pour établir des règles, vous verrez dans ce qui suit que nous utilisons lift lors de l’exploration des règles que l’algorithme renvoie.
Effectuer une analyse du Panier de marché dans R
Pour démontrer comment réaliser un MBA, nous avons choisi d’utiliser R et, en particulier, le package arules. Pour ceux qui sont intéressés, nous avons inclus le code R que nous avons utilisé à la fin de ce blog.
Ici, nous suivons le même exemple utilisé dans la vignette arulesViz et utilisons un ensemble de données de ventes d’épicerie qui contient 9 835 transactions individuelles avec 169 articles. La première chose que nous faisons est d’examiner les éléments des transactions et, en particulier, de tracer la fréquence relative des 25 éléments les plus fréquents de la figure 1. Cela équivaut à la prise en charge de ces éléments où chaque ensemble d’éléments ne contient que l’élément unique. Ce graphique à barres illustre les produits d’épicerie fréquemment achetés dans ce magasin, et il est à noter que le support des articles les plus fréquents est relativement faible (par exemple, l’article le plus fréquent ne concerne que 2,5% des transactions). Nous utilisons ces informations pour informer le seuil minimum lors de l’exécution de l’algorithme Apriori; par exemple, nous savons que pour que l’algorithme renvoie un nombre raisonnable de règles, nous devrons définir le seuil de support bien en dessous de 0,025.
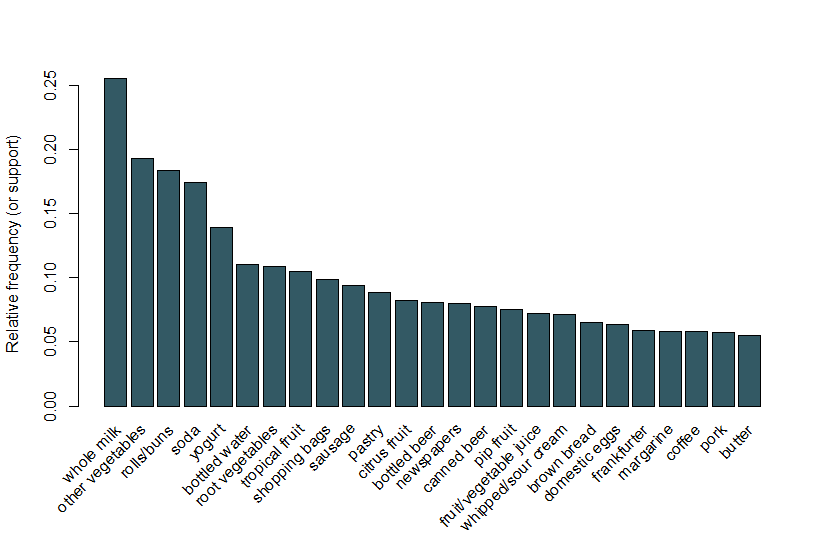
Figure 1 Un graphique en barres du support des 25 articles les plus fréquemment achetés.
En définissant un seuil de support de 0,001 et une confiance de 0,5, nous pouvons exécuter l’algorithme Apriori et obtenir un ensemble de 5 668 résultats. Ces valeurs de seuil sont choisies de sorte que le nombre de règles retournées soit élevé, mais ce nombre diminuerait si nous augmentions l’un ou l’autre des seuils. Nous recommandons d’expérimenter ces seuils pour obtenir les valeurs les plus appropriées. Bien qu’il y ait trop de règles pour pouvoir les examiner toutes individuellement, nous pouvons regarder les cinq règles avec la plus grande portance :
| Règle | Support | Confiance | Lift |
| {produits alimentaires instantanés, soda}=>{viande à hamburger} | 0,001 | 0,632 | 19,00 |
| {soda, popcorn}=> {snacks salés} | 0,001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. Par exemple, la première règle peut représenter le type d’articles achetés pour un barbecue, la deuxième pour une soirée cinéma et la troisième pour la cuisson.
Plutôt que d’utiliser les seuils pour réduire les règles à un ensemble plus petit, il est habituel qu’un ensemble plus grand de règles soit renvoyé afin qu’il y ait plus de chances de générer des règles pertinentes. Alternativement, nous pouvons utiliser des techniques de visualisation pour inspecter l’ensemble de règles retournées et identifier celles qui sont susceptibles d’être utiles.
En utilisant le package arulesViz, nous traçons les règles par confiance, support et lift dans la figure 2. Ce graphique illustre la relation entre les différentes métriques. Il a été démontré que les règles optimales sont celles qui se trouvent sur ce que l’on appelle la « limite support-confiance ». Essentiellement, ce sont les règles qui se trouvent sur la bordure droite de l’intrigue où le soutien, la confiance ou les deux sont maximisés. La fonction de tracé du package arulesViz dispose d’une fonction interactive utile qui vous permet de sélectionner des règles individuelles (en cliquant sur le point de données associé), ce qui signifie que les règles sur la bordure peuvent être facilement identifiées.
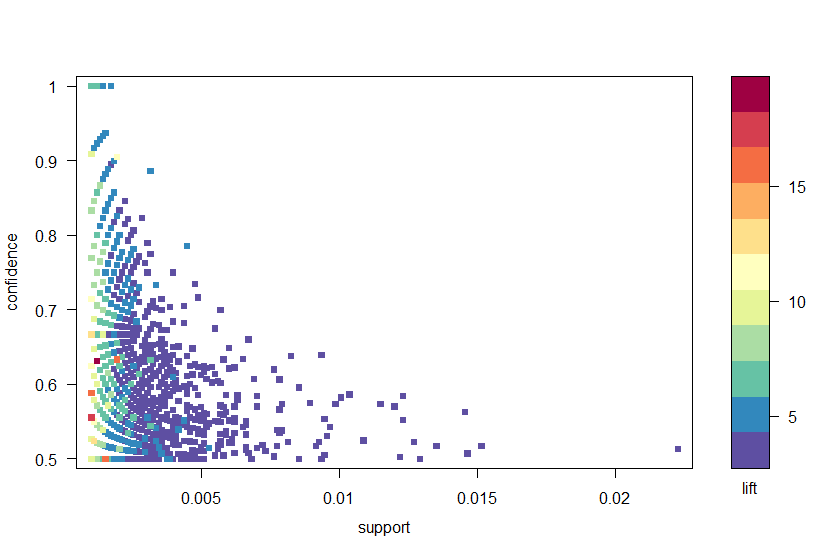
Figure 2 : Un nuage de points des métriques de confiance, de support et de lift.
Il y a beaucoup d’autres tracés disponibles pour visualiser les règles, mais une autre figure que nous recommandons d’explorer est la visualisation basée sur des graphiques (voir Figure 3) des dix premières règles en termes de portance (vous pouvez en inclure plus de dix, mais ces types de graphiques peuvent facilement être encombrés). Dans ce graphique, les éléments regroupés autour d’un cercle représentent un ensemble d’éléments et les flèches indiquent la relation dans les règles. Par exemple, une règle est que l’achat de sucre est associé à l’achat de farine et de levure chimique. La taille du cercle représente le niveau de confiance associé à la règle et la couleur le niveau de portance (plus le cercle est grand et plus le gris est foncé, mieux c’est).
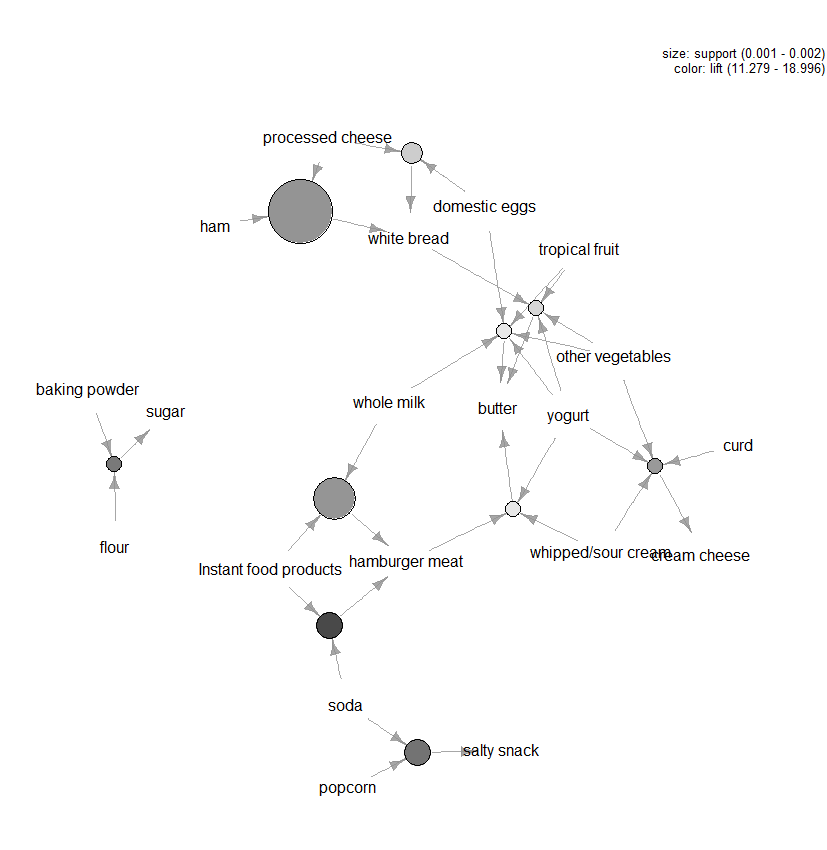
Figure 3 : Visualisation graphique des dix premières règles en termes de portance.
L’analyse du panier de marché est un outil utile pour les détaillants qui souhaitent mieux comprendre les relations entre les produits que les gens achètent. Il existe de nombreux outils qui peuvent être appliqués lors de la réalisation d’un MBA et les aspects les plus délicats de l’analyse sont la définition des seuils de confiance et de support dans l’algorithme Apriori et l’identification des règles qui valent la peine d’être poursuivies. Généralement, ce dernier est effectué en mesurant les règles en termes de métriques qui résument leur intérêt, en utilisant des techniques de visualisation et également des statistiques multivariées plus formelles. En fin de compte, la clé du MBA est d’extraire de la valeur de vos données de transaction en développant une compréhension des besoins de vos consommateurs. Ce type d’informations est précieux si vous êtes intéressé par des activités de marketing telles que des ventes croisées ou des campagnes ciblées.
Si vous souhaitez en savoir plus sur l’analyse de vos données de transaction, veuillez nous contacter et nous serons heureux de vous aider.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.