Les algorithmes de tri sont une combinaison maladroite de fondamentalement nécessaire et profondément controversée. Des nouveaux ingénieurs qui cherchent à impressionner lors d’une interview aux ingénieurs plus âgés à la recherche d’une solution à une base de données à échelle rapide, il existe une myriade de facteurs à prendre en compte. Quelle est la vitesse de comparaison entre deux objets ? Quel est le temps d’échange? Quelle est la taille de la base de données? Quel type d’objets contient-il ? Est-il déjà semi-trié? Les résultats doivent-ils être stables?

Chacune de ces questions peut tirer des arguments en faveur d’un algorithme ou d’un autre. Les données sources sont-elles volumineuses et complexes ? La plupart des langues utilisent par défaut le tri rapide standard avec sa complexité temporelle O (n log n). Est-ce plus petit? Le tri par insertion fonctionne à merveille sur ceux-ci. La plupart du temps triés? Zut, Le tri des bulles pourrait presque fonctionner pour cela. Si vous souhaitez lire / visualiser les mérites de chacun, consultez cette comparaison par toptal.com .

Un algorithme de tri que vous ne trouverez pas sur ce site, ou presque, est Tim Sort. Ce tri obscur est actuellement unique à Python et est utilisé comme algorithme de tri par défaut. Appelez array.sort en Python, et le tri Tim est ce qui est exécuté. Malgré cela, il est rare de trouver des ingénieurs qui connaissent et comprennent à la fois Tim Sort. Alors : qu’est-ce que c’est?

Tim Sort a été implémenté pour la première fois en 2002 par Tim Peters pour une utilisation en Python. Cela proviendrait de la compréhension que la plupart des algorithmes de tri naissent dans les salles de classe et ne sont pas conçus pour une utilisation pratique sur des données réelles. Tim Sort tire parti des modèles courants dans les données et utilise une combinaison de Tri par fusion et de Tri par insertion ainsi qu’une logique interne pour optimiser la manipulation de données à grande échelle.

Pourquoi Trier Tim?

En regardant la figure 2, nous pouvons immédiatement voir quelque chose d’intéressant. À son meilleur, Tim Sort surpasse le tri par fusion et le Tri Rapide. Au pire, il fonctionne à une vitesse comparable de tri par fusion et surpasse en fait le tri rapide. En d’autres termes, c’est étonnamment rapide.

En termes d’espace, le tri Tim est à la pire extrémité du spectre, mais la considération d’espace pour la plupart des algorithmes de tri est assez rare. O (n) n’est pas trop rude dans la plupart des cas; il convient de noter comme une lacune possible, et le seul endroit où le Tri rapide surpasse vraiment le tri Tim.

Le dernier élément sur lequel les algorithmes de tri sont souvent jugés est la stabilité. La stabilité est le concept selon lequel, lorsqu’ils sont triés, les objets de valeur égale conservent leur ordre d’origine. Maintenant, vous vous demandez peut-être pourquoi nous nous soucions de cela. Les articles sont de valeur égale — pourquoi cela nous dérange-t-il comment ils sont commandés?

La réponse simple est que la stabilité est importante pour les tris empilés. C’est-à-dire que vous triez d’abord en fonction d’un critère, puis en fonction d’un second. Si vous faites cela dans un algorithme instable, vous perdez instantanément toute fiabilité de votre premier tri lorsque vous exécutez le second. Pour référence, le Tri rapide est instable et le tri par fusion est stable.

Le tri Tim est également stable, sans parler du tri rapide s’il est légèrement lourd (par rapport au tri rapide uniquement). Bien que les algorithmes de tri puissent (et doivent) être jugés sur d’autres considérations, ce sont les trois grands.

L’Implémentation En Trois Étapes

Le Tri Tim est complexe, même selon les normes algorithmiques. La mise en œuvre est mieux décomposée en plusieurs parties.

Recherche binaire

La première chose dont vous avez besoin pour implémenter un tri Tim est une méthode de recherche binaire. Ceci est juste utilisé pour implémenter votre tri d’insertion plus tard.

Pour référence: Algorithmes de recherche binaire

Tri par insertion &Tri par fusion

Deuxièmement, vous devez coder le Tri par Insertion et le Tri par Fusion. Ce sont des algorithmes familiers et devraient être dans la poche arrière de la plupart des ingénieurs, mais nous allons examiner les principes fondamentaux de leur fonctionnement et pourquoi ils sont précieux pour nous ici.

Le tri par insertion est un algorithme de tri très basique. Il parcourt le tableau et chaque fois qu’il rencontre un élément en panne (strictement inférieur / supérieur à l’élément qui le précède), il le déplace dans la position appropriée dans le tableau déjà trié. Le tri par insertion est connu pour fonctionner très rapidement sur des tableaux déjà triés, ainsi que sur des tableaux plus petits. En fait, nous pouvons voir sur la figure 2 que le tri par insertion a un temps d’exécution impressionnant dans le meilleur des cas de O(n). Gardez à l’esprit aller de l’avant avec Tim Sort: le meilleur cas pour le tri par insertion est un tableau déjà trié. Cela peut sembler idiot, mais ce sera pertinent.

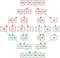
Le tri par fusion fonctionne d’autre part selon un principe de base: il est extrêmement facile de fusionner des tableaux déjà triés. Ainsi, il divise encore et encore un tableau de départ en deux jusqu’à ce qu’il ne s’agisse que d’éléments uniques. Ensuite, il reconstruit lentement le tableau principal en fusionnant ces éléments dans un ordre trié. Comme nous sommes partis de blocs de construction de taille un, il était très facile de créer des tableaux triés initiaux. Ensuite, il est facile de les fusionner. En fin de compte, nous passons O (n log n) temps, et (surtout) nous le faisons d’une manière qui est garantie stable.

Par exemple, voir :

Fusionner le tri: https://www.geeksforgeeks.org/merge-sort/

Tri par insertion: https://www.geeksforgeeks.org/insertion-sort/

Implémenter le Tri Tim

La clé pour comprendre l’implémentation de Tim Sort est de comprendre son utilisation des exécutions. Tim Sort exploite à son avantage les données pré-triées naturelles. Par pré-tri, nous entendons simplement que les éléments séquentiels augmentent ou diminuent tous (nous nous moquons de savoir lesquels).

Nous définissons d’abord une taille minrun. Ce que nous entendons par là, c’est que nous voulons nous assurer que toutes nos courses ont au moins une certaine longueur. Veuillez noter que nous ne garantissons pas que nous trouverons des pistes de cette taille — nous y reviendrons plus tard. Nous disons simplement qu’une course doit avoir au moins une certaine longueur.

Lorsque nous rencontrons une course, nous la mettons de côté. Lorsque nous trouvons l’exécution la plus longue dans une plage minrun. Nous avons maintenant une structure de données familière : un petit tableau trié. Si c’est au moins minrun en longueur, alors huzzah! Nous sommes prêts à passer à autre chose. Si ce n’est pas le cas, nous mettons en jeu le tri par insertion.

Vous vous souvenez peut-être d’en haut que le tri par insertion est particulièrement efficace sur deux types de tableaux: les petits et les déjà triés. Ce que nous venons de faire est un petit tableau trié. Si ce n’est pas au moins minrun en longueur, nous avançons et attrapons suffisamment d’autres éléments pour terminer l’exécution, puis utilisons le Tri par insertion pour les pousser dans notre tableau trié, rapidement et facilement. De toute évidence, si une exécution rencontre la fin du tableau, vous pouvez la laisser être un peu courte.

Une fois que vous avez créé toutes vos pistes (c’est-à-dire les sous-trames triées), vous utilisez votre tri de fusion pour les joindre ensemble. Dans le meilleur des cas, l’ensemble du tableau est déjà trié et Tim Sort est assez intelligent pour savoir qu’il n’a pas besoin de faire autre chose. D’autres fois, il a tendance à être extrêmement efficace. Comme avantage supplémentaire, le Tri par insertion et le tri par fusion sont stables, de sorte que le tableau résultant est stable.

Pour ceux qui préfèrent les balles:

1. Établissez une taille minrun d’une puissance de 2 (généralement 32, jamais plus de 64 ou votre Tri d’insertion perdra en efficacité)
2. Trouvez une exécution dans le premier minrun de données.
3. Si l’exécution n’a pas au moins minrun de longueur, utilisez le Tri par insertion pour saisir les éléments suivants ou antérieurs et les insérer dans l’exécution jusqu’à ce qu’elle ait la taille minimale correcte.
4. Répétez jusqu’à ce que le tableau entier soit divisé en sous-sections triées.
5. Utilisez la seconde moitié du tri de fusion pour joindre les tableaux ordonnés.

Conclusion

Le tri Tim est puissant. Il est rapide et stable, mais peut-être le plus important, il tire parti des modèles du monde réel et les utilise pour construire un produit final. Est-ce pour chaque situation? Probablement pas. Bonne chance de le programmer sur un tableau blanc lors d’une interview, et si vous avez juste besoin d’un algorithme de tri simple et rapide, vous ne voulez probablement pas vous embêter à implémenter quelque chose de si complexe. Cependant, pour les scientifiques des données qui analysent les chiffres, cela vaut plus que la peine d’y jeter un coup d’œil.

Pour les curieux, vous pouvez consulter l’intégralité du code de tri Tim sur github.

Merci

Merci à tous mes lecteurs. J’apprécie votre temps et j’espère sincèrement que vous avez trouvé le contenu instructif. Si vous avez des questions ou des réponses, n’hésitez pas à en déposer une ci-dessous.