La réfraction, ou flexion de la lumière, se produit lorsque la lumière passe d’un milieu à un autre avec un indice de réfraction différent. La réfraction est une caractéristique importante des lentilles, leur permettant de focaliser un faisceau de lumière sur un seul point, et est également responsable de divers phénomènes familiers, tels que la distorsion apparente d’objets partiellement immergés dans l’eau.

L’indice de réfraction est défini comme la vitesse relative à laquelle la lumière se déplace à travers un matériau par rapport à sa vitesse dans le vide. Par convention, l’indice de réfraction d’un vide est défini comme ayant une valeur de 1,0. L’indice de réfraction, n, des autres matériaux transparents est défini par l’équation:

où c est la vitesse de la lumière et v est la vitesse de la lumière dans ce matériau. Puisque l’indice de réfraction d’un vide est défini comme 1.0 et un vide est dépourvu de tout matériau, les indices de réfraction de tous les matériaux transparents sont donc supérieurs à 1,0. Dans la plupart des cas, l’indice de réfraction de la lumière dans l’air (1,0003) peut être utilisé pour calculer les indices de réfraction de matériaux inconnus. Les indices de réfraction de certains matériaux courants sont présentés dans le tableau 1 ci-dessous.

Matériau Indice de réfraction Air 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Par exemple, lorsque la lumière passe d’un milieu moins dense, tel que l’air, à un milieu plus dense, tel que l’eau, la vitesse de déplacement de l’onde électromagnétique diminue. Alternativement, lorsque la lumière passe d’un milieu plus dense à un milieu moins dense, la vitesse de l’onde augmente.

L’angle auquel la lumière réfractée se déplace, cependant, dépend à la fois de l’angle d’incidence et de la composition du matériau dans lequel elle pénètre. La normale peut être définie comme une ligne perpendiculaire à la frontière entre deux substances. La lumière passe dans la limite sous un angle par rapport à la normale et est réfractée selon la loi de Snell:

où n représente les indices de réfraction du matériau 1 et du matériau 2 et q symbolise les angles de lumière parcourant ces matériaux par rapport à la normale. Plusieurs points importants peuvent être tirés de cette équation. Lorsque n(1) est supérieur à n(2), l’angle de réfraction est toujours inférieur à l’angle d’incidence. Alternativement, lorsque n(2) est supérieur à n(1) l’angle de réfraction est toujours supérieur à l’angle d’incidence. Lorsque les deux indices de réfraction sont égaux (n(1) = n(2)), alors la lumière est traversée sans réfraction.

Le concept d’indice de réfraction est illustré à la figure 1 ci-dessous, en se concentrant sur le cas de la lumière passant de l’air à travers le verre et l’eau. Notez que si les deux faisceaux pénètrent dans le matériau plus dense par le même angle d’incidence par rapport à la normale (60 degrés), la réfraction du verre est presque 6 degrés supérieure à celle de l’eau en raison de l’indice de réfraction plus élevé du verre.

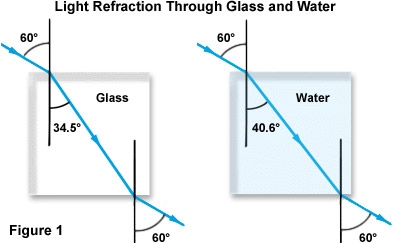
Les scientifiques ont découvert que l’indice de réfraction varie avec la fréquence du rayonnement (ou la longueur d’onde) de la lumière. Ce phénomène se produit en conjonction avec tous les milieux transparents et a été appelé dispersion. Par conséquent, lors de la mesure de l’indice de réfraction d’une substance transparente, la longueur d’onde particulière utilisée dans la mesure doit être identifiée. Ci-dessous, le tableau 2 détaille la dispersion de trois longueurs d’onde indépendantes dans différents milieux.

Matériel Bleu ( 486,1 nm) Jaune (589,3 nm) Rouge (656,3 nm) Verre couronne 1,524 1,517 1,515 Verre silex 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Cette lumière est appelée spectre de la raie D et représente la lumière jaune listée dans le tableau 2 ci-dessus. De même, les spectres des raies F et C correspondent à la lumière bleue et rouge de longueurs d’onde spécifiques émises par l’hydrogène. Ces spectres sont fondamentaux dans le calcul de la dispersion, qui peut être définie quantitativement comme :

où n est l’indice de réfraction du matériau à une longueur d’onde particulière désignée par D, F et C, qui représentent les raies spectrales du sodium et l’hydrogène comme discuté ci-dessus. La relation est telle que lorsque la longueur d’onde de la lumière augmente, l’indice de réfraction diminue. Cependant, de nombreux facteurs jouent un rôle dans la dispersion de divers matériaux, y compris leur composition élémentaire et moléculaire. Plusieurs solides inorganiques, tels que les chromates, les dichromates, les cyanures, les vanadates et les complexes d’halogénures, ont des dispersions inhabituellement élevées. Pourtant, les substituants organiques peuvent également contribuer à une dispersion élevée.

	Interactive Java Tutorial
Réfraction de la lumière Découvrez comment la longueur d’onde et l’angle d’incidence de la lumière affectent la réfraction dans une variété de milieux avec différents indices de réfraction.

Refraction of light is particularly important in the construction and physics of lenses. Rappelez-vous que lorsque le faisceau de lumière est sorti à la fois du verre et de l’eau de la figure 1, il a de nouveau été réfracté au même angle qu’il est entré dans le matériau. Ce concept est essentiel au fonctionnement des lentilles, bien que la forme de la lentille affecte de manière significative l’image résultante. Dans une lentille convexe, comme illustré ci-dessous sur la figure 2, les ondes lumineuses réfléchies par l’objet, en l’occurrence une girafe, sont courbées vers le centre optique de la lentille et convergent vers le point focal.

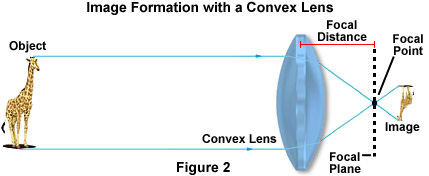
La position relative de l’objet par rapport au point focal avant de l’objectif détermine comment l’objet est imagé. Si l’objet est au-delà de deux fois la longueur du point focal, il apparaît plus petit et inversé et doit être imité par une lentille supplémentaire afin d’agrandir la taille. Cependant, lorsque l’image est plus proche de l’objectif que du point focal, l’image apparaît verticale et plus grande, comme on peut facilement le démontrer avec une simple loupe.

	Interactive Java Tutorial
Grossissement de l’image Explorez comment l’image d’une girafe est agrandie par la réfraction des ondes lumineuses traversant une lentille simple et mince bi-convexe.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Une simple paille dans un verre rempli d’eau, comme illustré à la figure 3, est un excellent exemple de cet événement. Dans cet exemple, les ondes de lumière doivent d’abord traverser l’eau, puis à travers la limite verre / eau, et enfin à travers l’air. Les ondes lumineuses réfléchies par les extrémités de la paille sont réfractées à un degré plus élevé que celles provenant du centre de la paille, ce qui fait apparaître la paille agrandie et légèrement déformée.

Le même phénomène peut être utilisé pour déterminer l’indice de réfraction d’un liquide avec un microscope optique. Pour ce faire, une cellule plate capable de contenir du liquide avec une marque (ou des graduations) doit être placée sur la surface intérieure du verre. De plus, l’un des oculaires de microscope doit comporter un réticule gradué inséré au niveau du plan d’image primaire pour les mesures de largeur de ligne de la marque dans la cellule plate. Avant d’ajouter le liquide d’indice de réfraction inconnu à la cellule, le microscope doit être focalisé sur la marque au bas de la cellule et une mesure de la position de la marque sur le réticule doit être notée. Ensuite, une petite quantité de liquide doit être ajoutée à la cellule et le microscope recentré sur la marque (à travers le liquide) et une nouvelle mesure prise. Le microscope doit ensuite être enfin focalisé sur la surface du liquide, et une troisième lecture enregistrée en mesurant la position de la marque sur le réticule. L’indice de réfraction du liquide inconnu peut alors être calculé à l’aide de l’équation suivante:

où D (mesuré) est la profondeur mesurée (de la surface du liquide à la position de la marque sur la cellule vide) à l’aide du microscope et D (apparent) est la mesure de la marque avec et sans liquide.

L’angle critique de réflexion est un autre concept clé dans l’étude de la réfraction de la lumière et est illustré ci-dessous dans la figure 4. Lorsque la lumière traverse un milieu à indice de réfraction élevé dans un milieu à indice de réfraction inférieur, l’angle incident des ondes lumineuses devient un facteur important. Si l’angle incident augmente au-delà d’une valeur spécifique (en fonction de l’indice de réfraction des deux milieux), il atteindra un point où l’angle est si grand qu’aucune lumière n’est réfractée dans le milieu d’indice de réfraction inférieur.

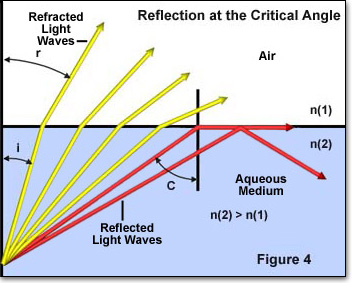
Sur la figure 4, les rayons lumineux individuels sont représentés par des flèches de couleur rouge ou jaune passant d’un milieu à indice de réfraction élevé (n (2)) à un indice de réfraction inférieur (n (1)). L’angle d’incidence de chaque rayon lumineux individuel est noté i et l’angle de réfraction par r. Les quatre rayons lumineux jaunes ont tous un angle d’incidence (i) suffisamment faible pour traverser l’interface entre les deux milieux. Cependant, les deux rayons de lumière rouge ont des angles incidents qui dépassent l’angle critique (environ 41 degrés) et sont réfléchis soit dans la limite entre les milieux, soit dans le milieu à indice de réfraction élevé. Ce phénomène se produit lorsque l’angle de réfraction (angle r sur la figure 4) devient égal à 90 degrés et que la loi de Snell se réduit à:

où (q) est maintenant appelé l’angle critique C. Si le milieu de moindre indice de réfraction est l’air(n= 1.00), l’équation se réduit encore à:

Comme discuté précédemment, une autre caractéristique importante de la réfraction de la lumière est que la longueur d’onde de la lumière a un impact sur la quantité de réfraction qui se produit dans un milieu. En effet, la quantité de réfraction qui a lieu est inversement proportionnelle à la longueur d’onde de la lumière incidente. Ainsi, la lumière visible de longueur d’onde plus courte est réfractée à un angle plus grand que la lumière de longueur d’onde plus longue. Par conséquent, lorsque la lumière blanche, qui est composée de toutes les couleurs du spectre visible, est passée à travers un prisme de verre, elle est dispersée dans ses couleurs constitutives d’une manière qui dépend des longueurs d’onde individuelles. La lumière visible à basse fréquence (600 nanomètres et plus) est réfractée à un angle plus petit que la lumière à haute fréquence, ce qui donne un effet semblable à un arc-en-ciel, comme illustré ci-dessous à la figure 5.

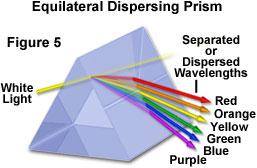
Ce même phénomène est également responsable de l’aberration chromatique. Lorsque la lumière blanche traverse une lentille convexe simple, plusieurs points focaux apparaissent à proximité qui correspondent aux différences d’indice de réfraction mineures des longueurs d’onde composantes. Cet effet a tendance à produire des halos colorés (rouges ou bleus, selon la mise au point) entourant les images des objets. La correction de cette aberration est généralement réalisée par l’utilisation de combinaisons de deux éléments de lentille ou plus composés de matériaux ayant des propriétés dispersives différentes, comme une lentille achromatique construite avec des verres à couronne et à silex.

	Interactive Java Tutorial
Réfraction par un prisme Examinez comment la lumière blanche est séparée en ses couleurs composantes par réfraction sous différents angles dans un prisme.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. L’exemple le plus courant est une caméra, qui est conçue pour créer des images nettes et focalisées sur une émulsion de film ou la surface d’un dispositif à couplage de charge (CCD) pour produire une image précise. D’autres dispositifs optiques qui exploitent ces caractéristiques de la lumière comprennent les microscopes et les télescopes, qui permettent de visualiser des objets invisibles à l’œil humain sans aide, qu’ils soient situés sur la tête d’une épingle ou dans une galaxie lointaine.

Auteurs contributeurs

Mortimer Abramowitz – Olympus America, Inc., Deux Lecteur de Centre d’entreprise., Melville, New York, 11747.

Shannon H. Neaves et Michael W. Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Université d’État de Floride, Tallahassee, Floride, 32310.

RETOUR À LA LUMIÈRE ET À LA COULEUR

Questions ou commentaires? Envoyez-nous un email.

© 1998-2021 par Michael W. Davidson et l’Université d’État de Floride. Tous Droits réservés. Aucune image, graphique, script ou applets ne peut être reproduit ou utilisé de quelque manière que ce soit sans l’autorisation des détenteurs des droits d’auteur. L’utilisation de ce site Web signifie que vous acceptez toutes les Conditions légales énoncées par les propriétaires.

Ce site Web est maintenu par notre équipe de programmation Web
Graphics&en collaboration avec la Microscopie Optique du Laboratoire National de Champ Magnétique Élevé.

Dernière modification : Vendredi 13 novembre 2015 à 14h18

Nombre d’accès Depuis le 10 mars 2003 : 181405

Visitez les sites de nos partenaires en éducation: